早期量子力学理论

黑体辐射

绝对黑体

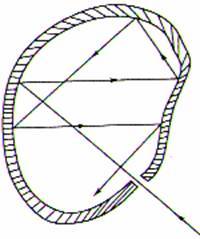
• 在不透明的空腔上开一个小孔, 外界辐射进入小孔后, 将会几乎被完全吸收, 可将小孔认为是绝对黑体
• 凡是易于吸收辐射的物体, 也一定是易于发出辐射的, 这样才能达到热平衡
• 因此加热空腔, 小孔将发出辐射, 称为绝对黑体辐射

黑体辐射定律

普朗克公式

• 谐振子 (带点粒子) 只能处在某些特殊状态, 他们的能量是某个最小能量单元 $\varepsilon$ 的整数倍
• 频率为 $\nu$ 的谐振子的最小能量单元正比于频率

$$\varepsilon=h\nu$$

• 谐振子能量交换的过程也不连续, 其放出与吸收的能量只能是 $\varepsilon$ 的整数倍

光电效应

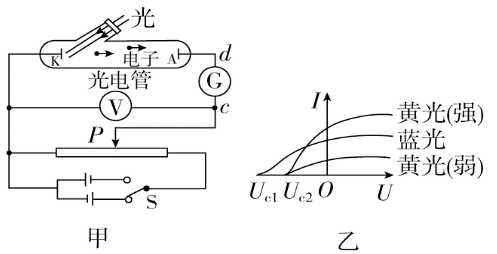
将单色光照到阴极板 $K$ 上, 并施加电压 $U$ , 记录电流计的读书 $I$

实验现象

1. 当正向电压足够大时, 阴极 $K$ 释放的电子全部飞到 $A$ 上, 电流 $I_m$ 最大, 且不再增大
2. 当反向电压足够大时, 全部电子无法达到 $A$, 电流最小, 此时的电压称为遏止电压 $U_a$

实验解释

• 单位时间内溢出的光电子数与入射光强成正比 (同 $\lambda$, 光强越大, 最大电流 $I_m$ 越大)
• 当电压达到遏止电压时, 此时电子从阴极溢出时具有的初动能全部用于克服电场力做功

$$E_{k max}=\frac{1}{2}mv^2_{max}=e|U_a|$$

• 光电子的初动能与入射光的频率成线性关系, 频率越高, 初动能越大

$$|U_a|=k\nu-U_0$$

• 要产生光电效应, 入射光的频率必须大于截止频率, 与光强无关

$$\nu=\frac{|U_a|+U_0}{k}$$

• 当满足截止频率条件, 一旦有光照, 就立即产生光电效应

爱因斯坦方程

• 每一个光子具有能量

$$\varepsilon=h\nu$$

• 光子具有不同能量, 光照强度取决于单位时间通过单位面积的光子数
• 电子吸收光子, 获得能量 $\varepsilon=h\nu$后
  1. 一部分用于逃逸原子, 称为逸出功 $A$
  2. 另一部分称为初动能, 满足

  $$h\nu=\frac{1}{2}mv^2+A$$

波粒二象性

• 从相对论角度推导能量与动量
• 光子的能量满足

$$E=h\nu=mc^2$$

• 光子的质量满足

$$m=\frac{h\nu}{c^2}$$

• 光子的动量满足

$$p=mc=\frac{h\nu}{c}=\frac{h}{\lambda}$$

康普顿效应

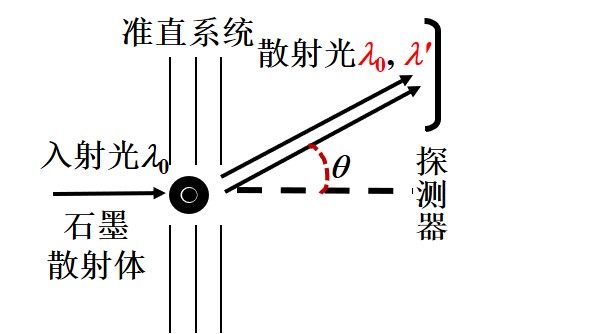
波长为 $\lambda_0$ 的X射线通过散射物质后, 将沿各个方向发射出散射射线

实验现象

1. 散射射线的波长除 $\lambda_0$ 外, 还有波长 $\lambda>\lambda_0$ 的射线
2. 波长差 $\Delta\lambda=\lambda-\lambda_0$ 随散射角 $\theta$ 增大而增大

实验原理

• 光子与电子发生了碰撞, 且满足能量守恒, 动量守恒与相对论
• 推导得到 $\Delta\lambda$ 满足公式

$$\Delta\lambda=\frac{h}{m_0c}(1-\cos\theta)=\lambda_c(1-\cos\theta)$$

其中 $\lambda_c\approx 2.43\times 10^{-12}m$, 可从计算器中调用

波尔原子论

基本假设

定态假设

电子在轨道上绕核运动 (匀速圆周运动, 存在向心加速度), 原子具有一定的能量 $E_n$ 而不会发生辐射, 处于稳定的运动状态

轨道角动量量子化条件

根据德布罗意的驻波条件有 (环形上的驻波, 与直线驻波条件不同)

$$2\pi r=n\lambda$$

因此只有当电子的角动量满足量子化条件的轨道才是稳定的

$$L=mvr=\frac{h}{\lambda}r=n\frac{h}{2\pi}(n=1,2,\dots)$$

跃迁定则

当电子从具有较大能量的轨道 $n$ 跃迁到能量较低的轨道 $k$ 时, 将以光子的形式释放能量, 其频率满足

$$\nu=\frac{E_n-E_k}{h}$$

氢原子的能量

• 更具氢原子结构可得, 电子的能量包含动能与电势能
• 将无穷远处作为电势能的零点, 计算可得基态轨道 ($n=1$) 能量最小, 满足 $E_1=-13.6eV$
• 其他轨道则满足

$$E_n=\frac{E_1}{n^2}(n=1,2,\dots)$$

氢原子光谱

氢原子向下越前发出光子时, 不一定直接到达基态, 可能先到达一个较低的能级再跃迁到基态, 计算氢原子光谱时要注意

量子力学

波函数

自由粒子的波函数

• 根据波动性, 则其可以被 (复变) 波函数描述

$$\Psi(x,t)=\Psi_0e^{-i2\pi(\nu t-x/\lambda)}$$

• 使用波函数的相位描述粒子性, 代入波函数中
  1. 能量满足 $E=h\nu$
  2. 动量满足 $p=\frac{h}{\lambda}$
  3. 定义 $\hbar=\frac{h}{2\pi}$
• 可得到自由粒子的波函数为

$$\Psi(\vec{r},t)=\Psi_0e^{-\frac{i}{\hbar}(Et-\vec{r}\cdot\vec{p})}$$

叠加态原理

当体系有一系列可能的状态 ${\Psi_1,\Psi_2,\dots}$, 则 $\Psi=C_1\Psi_1+C_2\Psi_2+\dots$ 也是一个可能的状态

波函数意义

• 波函数在点 $\vec{r}$ 处出现的概率与 $|\Psi|^2$ 成正比, 满足

$$dP=|\Psi(\vec{r},t)|^2 dv$$

• 定义概率密度函数

$$\rho(\vec{r},t)=\frac{dP}{dv}=|\Psi(\vec{r},t)|^2=\Psi\cdot\Psi^*$$

• 波函数模的平方作为概率密度函数, 因此要求波函数满足标准化条件
  1. 单值
  2. 有限
  3. 连续 (一阶导数连续)

波函数归一化条件

• 波函数模的平方作为概率密度函数, 需要满足概率密度的归一化条件 (一维情况)

$$\int_{-\infty}^{\infty}|\Psi(x,t)|^2dx=1$$

• 当波函数不满足归一化条件时, 可以引入系数 $C$, 使之满足归一化条件, 称 $C\Psi(x,t)$ 为归一化波函数
• 系数 $C$ 的计算方法 (注意平方)

$$\frac{1}{C^2}=\int_{-\infty}^{\infty}|\Psi(x,t)|^2dx$$

不确定原理

• 观察微观粒子时, 其坐标的不确定量与动量的不确定量满足

$$\Delta x\cdot\Delta p_x\ge\frac{\hbar}{2}$$

• 其时间的不确定量与能量的不确定量满足

$$\Delta t\cdot\Delta E\ge\frac{\hbar}{2}$$

薛定谔方程

通过问题的边界条件与初始条件解出粒子波函数的方程

定态薛定谔方程

• 当势能 $V=V(x)$ 仅与坐标有关, 与时间无关时 (电势场), 有定态薛定谔方程

$$-\frac{\hbar^2}{2m}\frac{d^2\psi}{dx^2}+V(x)\psi(x)=E\psi(x)$$

• 薛定谔方程的一种解为

$$\Psi(x,t)=\psi(x)e^{-\frac{i}{\hbar}Et}$$

• 称 $\psi(x)$ 为定态波函数, 体现振幅随位置的变化
• $e^{-\frac{i}{\hbar}Et}$ 体现了波在各个点上的简谐振动, 称为时变因子

一维无限深势阱

• 对于一维无限深势阱, 满足

$$V(x)=\begin{cases}0&,0<x<a\\\infty &,x\le 0,x\ge a\end{cases}$$

• 可得粒子不可能到达势阱外, 因此 $\psi(0)=\psi(a)=0$
• 由于势阱内 $V(x)=0$, 根据定态微分方程

$$\frac{d^2\psi}{dx^2}+k^2\psi=0$$

• 微分方程符合简谐振动的微分形式, 因此假设

$$\psi(x)=A\sin kx$$

• 为了满足边界条件 (类似直线驻波) $\psi(a)=0$, $k$ 值将被限制

$$ka=n\pi(n=1,2,\dots)$$

• 为了满足归一化条件, $A=\sqrt{\frac{2}{a}}$
• 最后得到定态波函数为

$$\psi(x)=\begin{cases}\sqrt{\frac{2}{a}}\sin\frac{n\pi x}{a}&,0<x<a\\0 &,x\le 0,x\ge a\end{cases}$$

一维无限深势阱定态波函数的推论

• 由于 $k^2\propto E$ , 在一维无限深势阱中, 粒子的能量只能取一系列分立的值, 称为能量本征值

$$E=\frac{n^2\pi^2\hbar^2}{2ma^2}(n=1,2,\dots)$$

• 根据波函数可得, 粒子出现在各点的概率是不均匀的
• 当量子数 $n$ 足够大时, 近似均匀出现, 与经典理论相符

一维势垒

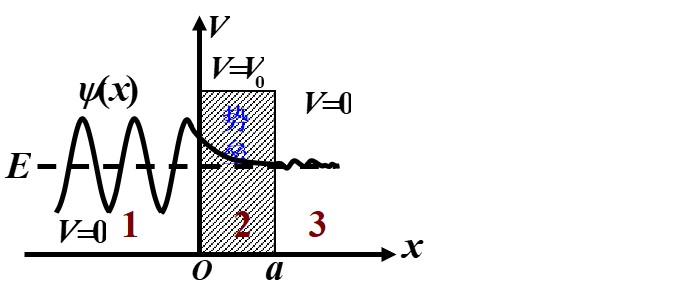
1. 能垒左侧是电子物质波入射波与反射波的合成
2. 在能垒中, 电子出现的概率密度按指数减小, 当 $L$ 不大, 仍有概率出现在能垒右侧
3. 因此电子有一定的概率在能垒的右侧被检测到
4. 通过能垒需要克服能量, 低于能垒的电子能够通过说明量子力学中的粒子总能量属于统计量

氢原子问题

能量量子化

• 主量子数 $n=1,2,3,\dots$
• 氢原子的能量

$$E_n=\frac{E_1}{n^2}(E_1=-13.6eV)$$

轨道角动量量子化

• 角量子数 $l=0,1,2,\dots,n-1$
• 电子角动量

$$L=l\sqrt{l+1}\hbar$$

• 不与特定的轨道对应, 对于一个 $n$ 有 $n$ 个取值

角动量的空间量子化

• 轨道磁量子数 $m_l=0,\pm 1,\pm 2,\dots,\pm l$
• 电子的角动量在空间的取向不是任意的, 其在 $z$ 轴的投影为

$$L_z=m_l\hbar$$

• 确定角动量的取向, 对于一个 $l$ 其角动量有 $2l+1$ 个取向

电子自旋

• 自旋量子数 $z=\frac{1}{2}$

• 确定了电子自旋角动量的大小为 $L_s=\sqrt{s(s+1)}\hbar=\frac{\sqrt{3}}{2}\hbar$

• 自旋磁量子数 $m_s=\pm\frac{1}{2}$

• 电子自旋的角动量是量子化的, 且取向也不是任意的, 且在 $z$ 轴方向的投影值只有两个

$$L_{sz}=m_s\hbar$$

• 对于一个电子, 有两种自旋状态

泡利不相容原理

• 原子系统中不可能有两个或以上状态相同的电子, 因此对于一个 $n$, 共能对应 $2n^2$ 个电子
• 将原子中主量子数相同的电子属于一个壳层

半导体与激光

激光

激光原理

1. 通过提供能量, 使大量原子处于相同激发态
2. 其中一个原子自发辐射
3. 被另一个同激发态的受激吸收, 受激辐射, 发出两个状态相同的光子
4. 不断重复, 持续发出大量状态相同的光子

产生激光的条件

1. 激励能源 (使原子激发)
2. 粒子数反转 (有合适的亚稳态能级)
3. 光学谐振腔 (方向性, 光放大, 单色性)

光学谐振腔的作用

由一个全反射镜与一个部分反射镜组成

1. 使激光具有极好的方向性
2. 增强光放大作用
3. 使激光具有极好的单色性

导体

1. 导体中的原子的电子云相互重叠, 电子在整个晶体上运动
2. 部分能级相互叠加, 形成能带, 可以容纳一定能量范围的, 数量固定的电子
3. 对于没有填满的能带, 电子容易在能带中跃迁, 并最终形成电流

导体的能带结构

1. 价电子 (外层电子) 所在的能带称为价带
2. 填满电子的能带称为满带
3. 完全没有电子的能带称为空带
4. 能带之间的间隔称为禁带, 电子不能进入, 能够阻止电子的跃迁

导体

1. 价带没有填满
2. 价带被填满但与空带重叠或相连

绝缘体

• 绝缘体的价带为满带且与相邻的空带之间的禁带较宽, 电子很难激发到空带上
• 在强电场的作用下可能使电子能够跃入空带, 形成导体

半导体

半导体与绝缘体类似, 但禁带宽度小得多

N 型半导体

1. 在半导体中掺入少量五价元素
2. 额外的价电子的能级在禁带上靠近空带的位置, 称为施主能级
3. 施主能级的电子很容易被激发到空带上, 并以负电的电子为载流子导电

P 型半导体

1. 在半导体中掺入少量三价元素
2. 缺少的价电子的能级在禁带下靠近满带的位置, 形成空穴, 称为施主能级
3. 满带的电子很容易被激发到施主能级的空穴, 并以正电的空穴为载流子导电

原子核物理

原子核

原子核的组成

1. 质子数 $Z$
2. 中子数 $N$
3. 核子总数 $A=Z+N$
4. 核素符号 ${^{A}_{Z}X}$

结合能

• 核素 (原子) 的质量总是小于组成其核子 (中子, 质子) 的总质量, 存在质量差 $\Delta m$
• 定义结合能, 用于度量核素的稳定性

$$B=\Delta mc^2=(Zm_p+Nm_n-m_x)c^2$$

• 定义比结合能 $\varepsilon$, 比结合能越大, 表示原子结合越稳定

$$\varepsilon=B/A$$

原子衰变

天然放射性元素的衰变方式

1. $\alpha$ 衰变——从核中放出 $\alpha$ 粒子的过程
   • 电离本领最强
   • 贯穿物体的本领最强
2. $\beta$ 衰变——核中放出电子的过程
3. $\gamma$ 衰变——从核中放出光子的过程
   • 电离本领最弱
   • 贯穿物体的本领最弱

放射性衰变的规律

放射性衰变的指数规律

$dt$ 时间内, 发生衰变的原子数为 $-dN$, 正比于当前存在的原子核数目 $N$, 表达式为

$$-dN=\lambda Ndt$$

积分后可得原子数目变化规律为

$$N=N_0e^{-\lambda t}$$

放射性活度

实验上, 无法直接测量原子数目, 只能测得单位时间内发生核衰变的次数, 称为放射性活度

$$A=\frac{-dN}{dt}=\lambda N=A_0e^{-\lambda t}$$

半衰期

定义放射性活度下降到一般所用的时间为半衰期 $T_{1/2}$ 满足

$$T_{1/2}=\frac{\ln 2}{\lambda}$$

放射性原子核平均寿命

使用 $\tau$ 表示, 计算存在时间与个数的加权平均, 带入公式的微分得到

$$\tau=\frac{1}{N_0}\int tdN=\frac{1}{\lambda}$$