光学
电磁波理论
惠更斯原理
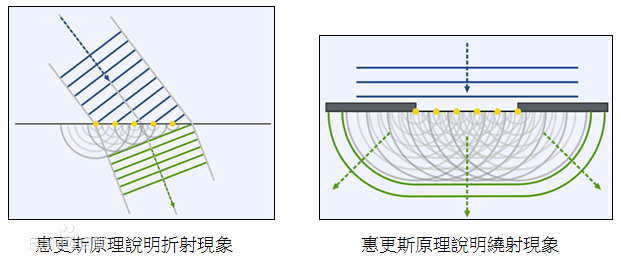
波面上的各点都可以看成产生子波 (球面波) 的波源, 这些子波的包络面可以看成新的波面
波的折射
- 波在入射两种介质的界面时, 将会产生折射
- 这是由于波在两种介质的速率不同导致的
- 如图, 平面波在界面上产生的子波在新介质中传播速率减慢, 导致最先产生的子波波面与最后到达的子波源切线改变, 导致波面的法向改变
- 对于入射角 i, 折射角 γ, 有折射定律
nisini=nγsinγ
光波性质
- 光是电磁波, 其在真空中的传播速度最快, 且为常量 c, 因此有
c=λν
- 将光速与光波在透明介质传播速率的比值定义为折射率
n=vc>1
- 光波中 E 与 H 垂直, 使用 E 表征光波, 将 E 的振动称为光振动
- 沿 x 方向的平面光波可表示为
E(x,t)=E0cos(ωt−λ2πx+φ0)
- 人眼直接观察到的为光强, 即光波的平均能流密度满足 I∝E02
- 由于原子辐射具有随机性与间歇性, 因此一般光源的 ω,φ0 仅持续极短的 Δt≈10−9s, 并且随时间在一个区间内快速变化
- 根据傅里叶分析可得
Δν⋅Δt=1
光源的持续时间越短, 频率的变化范围越大
- 定义波列 L=cΔt, 表现出光源发出的一列稳定光波的长度
光波叠加
同频率光波叠加类似同频率简谐波的叠加, 满足旋转矢量的平行四边形叠加的余弦定律
E122=E102+E202+2E10E20cosΔφ
其中
Δφ=−λ2πx1+φ10+λ2πx2−φ20
为两列波的相位差(包括路程与初相位)
在人眼观测中, 光波叠加为一段时间内的平均光强, 积分计算可得
I∝E2=I1+I2+2I1I2⋅cosΔφ
非相干叠加
对于两个普通光源, 其 φ0 无关系, 并且不断变化, 因此认为 cosΔφ=0, 两个普通光源的光波叠加后 I=I1+I2
相干叠加
当叠加光波相干(如来自同一个光源), 此时两列波 φ0 相同, 波程差来自光程 x, 因此对于一个点, cosΔφ=C, 并在平面上显现出明暗相间的干涉条纹
可得明暗条纹的条件为
Δφ={±2kπ,±(2k+1)π,明条纹暗条纹(k=±0,1,2,…)
相干条件
- 各光波频率相同
- 各光波有平行分量(能够投影到一个平面上)
- 由于光为横波, 两列光波的光矢量在空间中不一定平行, 需要将其中一个光矢量投影到另一个上计算
- 垂直分量的光矢量构成背景光
- 当光矢量垂直, 则不构成相干光
- 光振动的相位差保持稳定(从同一光源分光或使用激光源)
光程
- 无论在何种介质中, 光波的频率 ν 始终不变, 但波长 λ 与波速 v 改变, 因此, 介质中的波长为
λn=nλ
- 因此当一列光波经过了不同介质后, 与光源的相位差为
Δφ=−(λ12πr1+λ22πr2)=−λ2π(n1r1+n2r2)
- 定义光程 d
dk=∑niri
- 因此初相位相同的相干光源的相位差为
Δφ=λ2π(d2−d1)=λ2πδ
带入 λ2πδ=Δφ
δ={λk,λ(k+21),明条纹暗条纹(k=±0,1,2,…)
物象间等光程性
- 光学仪器 (透镜, 球镜) 的物点 (光源) 和像点 (焦点) 之间的各个光线光程相同
- 对于平行光源, 在垂直于光线的平面内相位相同, 来自无穷远处的光源
- 认为平行光聚焦于无穷远处, 来自无穷远处的光源
半波损失
- 光从波疏介质到波密介质时
- 当入射角 i≈90∘ 或 i≈0∘
- 反射光与入射光的相位将相差 2π
光介质
- 将折射率 n 大的物质称为波疏介质 (如平面镜, 玻璃)
- 将折射率 n 小的物质称为波密介质 (如真空, 空气)
- 当出现平面镜时, 很有可能发生半波损失
分波阵面干涉
杨氏干涉
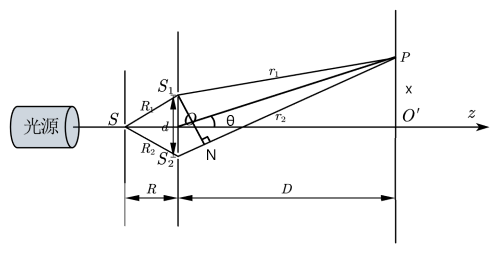
子光源 S1,S2 来自同一个光源(波阵面), 因此为相干光, 当SS1=SS2 时, 两个子光源在 P 点的光程差为
δ=r2−r1≈S2N≈dsinθ≈dtanθ=dDx
其中 D≫d,x;θ≈0
x 体现了屏幕上 p 点的明暗情况, 因此有
x={λdDk,λdD(k+21),明条纹暗条纹(k=0,±1,2,…)
k 为条纹级数, k=0 为零级明条纹
其中屏幕上两明条纹 / 暗条纹间距相同
Δx=λdD
因此条纹间距与光路中是否有介质无关
但光路中的介质将改变 δ, 导致条纹移动
光强分析
(推导见双缝衍射)
IP=4I1cos2(2Δφ)
2β=Δφ=λ2πdsinθ
劳埃德镜

- 可将 S1 在平面镜中的的虚像视为相干光源光源 S2, 即杨氏干涉中的第二条狭缝
- 由于光线从空气入射平面镜将产生半波损失, 因此干涉条纹的明暗与杨氏干涉相反
- 由于光源为虚光源, 因此条纹只有上半部分, 级数 k≥0
时间相干性
杨氏干涉中, 当两列光的光程差 δ>L=cΔt 时, 即两列光虽然分自同一个光源, 但两列光相差时间过长, 光源的 ω 与 φ0 以发生变化, 不再相干, 称为时间相干性
普通光源中, 由于波列长度(相干长度) L 极小, 因此产生相干的 δ 较小, 相干性较差
空间相干性
杨氏干涉中, 缝光源 S 也具有宽度 b, 在缝宽边缘也可视为另一个光源 S′, 也会通过双缝产生干涉条纹
由于 S′ 到双缝距离 Ri 不同, 会产生附加光程差
δb=R2−R1≈2Rbd
其中 R 为单缝与双缝的垂直距离
如果 δb=2λ, 缝边缘产生的干涉条纹与中心产生的条纹恰好相反, 将导致干涉条纹消失, 因此定义
2Rb0d=2λ
仅当光源的 b<b0 才能产生可观察到的干涉条纹, 可以此筛选特定的 λ 或 b
分振幅干涉
- 即利用光的反射与折射获取相干光源的干涉
- 由于利用了反射与折射, 需要注意半波损失
等倾干涉
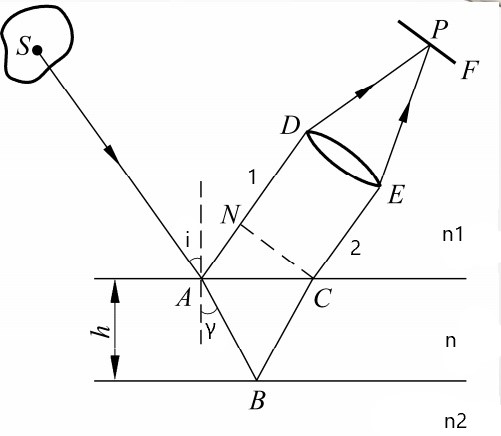
- 将分解光源的两层薄膜平行的干涉称为等倾干涉
- 由于两列相干光平行, 因此认为相遇于无穷远处, 或需要透镜聚焦
- 注意薄膜介质与薄膜两侧介质的折射率 n, 可能会在 A,B 处产生半波损失
等倾干涉分析
根据折射定律
n1sini=nsinγ
在不考虑半波损失的条件下 (n1<n<n2, 两光路均有半波损失), 如图可得 (完整公式不要求)
δ=n(AB+BC)−n1AN=2ndcosγ=2dn2−n12sin2i
k 级亮条纹满足
δ=2dn2−n12sin2i=kλ(k=1,2,…)
对于点光源 S, 可得到以下规律
- 干涉条纹仅与入射角 i 有关, 因此称为等倾干涉, 当 S 为点光源时, 入射角为 i 的点可构成一个圆, 从而产生明暗相间的圆形干涉条纹
- 越靠近中心, i 越小, 条纹级数越高 (sini 项为负), 相应的, 边缘级数小
- 增大 d 时, δ 增大, 中心圆环的级数增大, 表现为圆环从中心涌出
- 根据 δ=2ndcosγ=kλ, 边缘条纹的级数 k 较小, 对应的 γ 较大, 根据 y=cosθ 的图像可得, 边缘条纹的级数变化快, 间距窄, 中心条纹间距宽, 条纹稀疏
对于平行光源 S
- 当 S 为平行光源时, 各个入射点 i 相同, 只能得到一个条纹/点
- 对于垂直入射的自然光, δ=2dn, 表现为部分 λ 干涉极大, 部分干涉极小 (肥皂泡原理)
对于不同的介质与观察方向
- 当仅有一个界面发生半波损失时, 需要在光程中考虑附加光程差 δ′=2π, 如 n1,n2>n, 此时将得到相反的图样
- 从反方向观察, B 处折射光与 C 处反射再折射光也将产生等倾干涉, 并且条纹与正面观察的相反 (由于半波损失情况与正面相反导致, 符合能量守恒)
等厚干涉
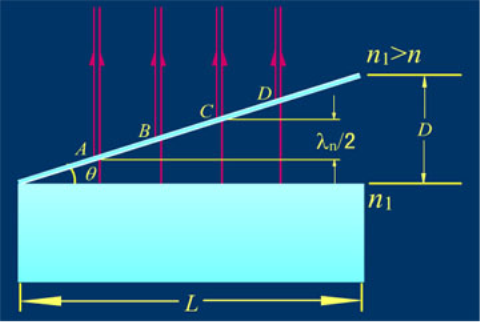
- 将分解光源的两层薄膜成一定角度的干涉称为等厚干涉
- 实际问题中, 只讨论 i=0 即垂直入射的情况
- 由于厚度相同的位置干涉情况相同, 因此称为等厚干涉
- 等厚干涉中, 相干光的光程差为 δ=2nd (经历了折射与反射, 需要记两倍的厚度 d)
劈尖干涉
当 θ≈0, 沿斜边距离棱角 l 处的光程差为
δ=2nltanθ≈2nlθ=kλ(亮条纹)
干涉中相邻的条纹距离为
Δl=2nθλ
一般劈尖中心为空气, n=1
根据等候干涉的特点, 一条连续条纹对应的厚度相同, 因此可以此判断薄膜表面的凹陷
当上下表面为玻璃, 中间为空气时, 存在半波损失, 需要注意半波损失
增透膜
确定薄膜厚度, 使反射光为干涉极小, 增大透射光光强
牛顿环
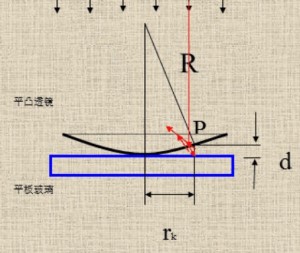
r2=2Rd−d2≈2Rd
- 由于牛顿环中透镜与平板为玻璃, 因此存在半波损失
- 因此可得暗环半径满足 (空气 n=1) $$r=\sqrt{kR\lambda}(k=0,1,2,\dots)$$
- 与等倾干涉不同, 越接近外层, 条纹级数越大
- 与等倾干涉类似, 越接近外层, 条纹越密
- 由于 k=0,r=0, 因此中心条纹为暗纹 (仅当中心紧贴着下表面时成立)
迈克尔逊干涉仪
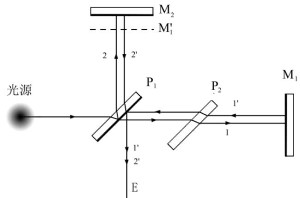
- 引入补偿板 P2, 使两束光均经过两次透光板, 保证两束光除空气外光程相同
- 干涉仪将光源分为折射 1 与反射 2 两束, 一束来自可动镜 M2, 另一束来自固定镜 M1, 其虚像 M1′ 与 M2 平行
- 假设 M1′ 与 M2 距离相同, 由于光束在反射镜来回一次, 因此两束光的光程差为 δ=2dn, 通过移动 M2, 改变光程差与成像
- 可通过此方法, 已知 λ, 计算 Δd
- 已知 Δd, 计算 λ
- 当光源为点光源 (散射面光源), 得到等倾干涉的圆形图样
- 当 M1′∦M2, 光源为平行光, 得到等厚干涉图样
夫琅禾费衍射
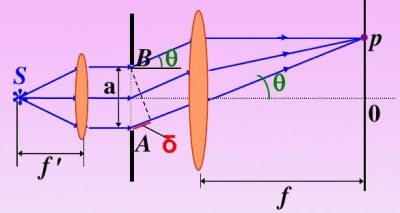
- 根据惠更斯原理, 光波在狭缝处可分解为无数个子光源, 光屏上的点 P 为子光源共同聚焦的结果
- 当入射狭缝的光源为平行光时, 称为单缝夫琅禾费衍射
- 无论单缝位置在哪, 衍射图像主要与透镜的位置有关, 其中 θ 为光屏上 P 点与透镜中心及中心线所成的角
叠加法推导单缝夫琅禾费衍射
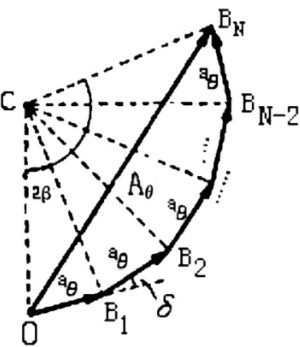
- 将子光源在 p 点的光振动以相量形式表示为 dB=dE∠dφ0
- 由相邻光振动的光程差 dδ≈dxsinθ 可得
dφ0=λ2πdδ=λ2πdxsinθ
E0=∫dEφ′=∫dφ0=λ2πasinθ
- 因此振动相量叠加后为一圆弧, 弧长为 E0, 圆心角为 φ0′, 在 p 点的振动相量 B 为弧的弦, 定义 α=φ′/2=λπasinθ , 因此叠加振幅
E=2φ′E0⋅sin2φ′=αE0sinα
- 根据惠更斯原理, E0∝a, 因此最大光强与缝宽成正比
夫琅禾费衍射光强分析
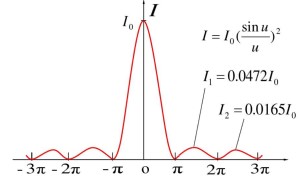
实际分析中通常分析光强分布
I∝E2=I0(αsinα)2
其中, I0∝a2, 最大光强与缝宽的平方成正比
- 定义 α=0 为中央主极大, 亮度最高
- 定义 k 级次极大位置为(注意 k 不可取 0)
α=(k+21)π(k=±1,2,3,…)
α=kπ(k=±0,1,2,…)
- 由于 θ≈0, 因此 α=λπasinθ≈λπaθ 定义中央主极大到一侧的暗纹宽度为中央主极大的半角宽
Δθ=αλ
- 当透镜到屏幕距离为 f 时, 屏幕上中央主极大的线宽为
Δx=2ftanΔθ≈2fαλ
- 综上可得, 单缝缝宽 a 越小, 主极大亮度 I0 越低, 但宽度 Δx 越大
半波带法
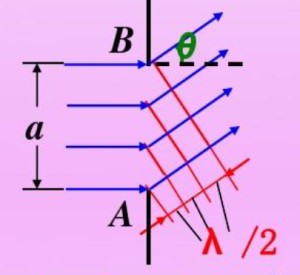
- 将缝宽向光线方向的投影以宽度 λ/2 等分, 反过来将入射光源分为 n 部分
- 各部分子光源间的光程差为 λ/2, 因此每两部分的光线相干抵消, 最终叠加得到暗条纹
- 因此假设 asinθ=πλα=nλ/2
- n=0, 所有子光源的光程差为 0, 为主极大
- n 为偶数, 子光源相互抵消, 为暗纹
- n 为奇数, 至少有一部分子光源没有被抵消, 为次极大
双缝衍射与干涉
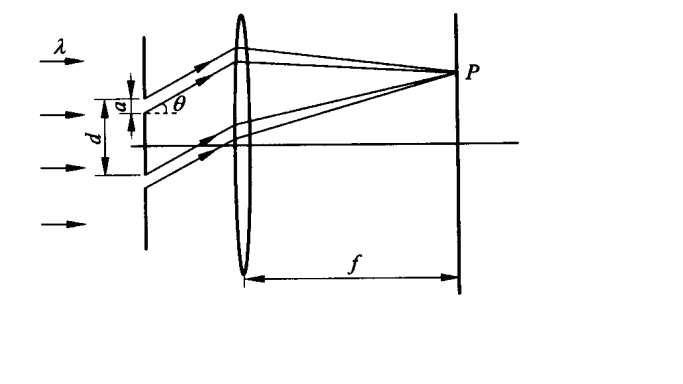
- 由于单缝衍射的图样与单缝位置无关, 因此两缝产生的条纹完全重合, 但光程差不同
- 两图样的叠加可通过双缝干涉的方法计算
- 设双缝中心距 d, 双缝缝宽 a
双缝衍射的光强分布推导
4I1=4I2=I0∝E102=E202
IP=I1+I2+2I1I2cosΔφ=2I1(1+cosΔφ)=4I1cos2(2Δφ)
- 其中光程差通过做垂线的方法可得 (不带入双缝干涉的近似式)
2β=Δφ=λ2πdsinθ
- 再考虑衍射的作用, 有 I0′=I0(αsinα)2
- 得到双缝衍射的光强公式
I=I0(αsinα)2cos2β
其中
α=aλπsinθ
β=dλπsinθ
双缝衍射的图样特点
- 当 θ=0, I=I0 光强最大
- 衍射中央明文角宽度 Δθ=a2λ, 干涉中央明文角宽度 Δθ′=dλ
- 由于 d>a, 因此 Δθ>Δθ′, 条纹的明暗由干涉决定, 与干涉明暗纹的条件相同
- 当衍射极小时, asinθ=k′λ; 当干涉极大时, dsinθ=kλ, 当两者相等时有 k=k′ad, 其中 k 为明条纹的级数, k′ 为衍射因子第 k 级极小, 当 k 满足此条件时, 称 k 为缺级, 可以根据缺级的位置, 判断 ad 大小
- 根据对称性, 左右两第 k 缺级中, 共会有 2×(k−1)+1 条条纹
衍射光栅
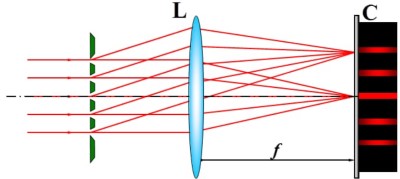
- 设光栅常量即两缝中心距 d, 双缝缝宽 a, 共有 N 条狭缝
叠加法推导衍射光栅

- 每个狭缝产生的衍射图样重合, 且条纹之间的光程差均为 Δφ=λ2πdsinθ, 光矢量振幅均为 Ei=E0αsinα
- 因此也可以对各个狭缝在 P 点的光振动相量叠加, 得到一个圆弧, 实际光振动相量即圆弧的弦 BN
- 将圆弧中的三角形 ΔCOB1 视为等腰三角形, CO 为圆弧半径, 认为三角形顶角为 Δφ≈0
- 因此圆弧半径 r=sin(Δφ/2)Ei/2
- 圆弧圆心角为 NΔφ
- 对弦三角形 ΔCOBN, 可以解出
EN=2rsin(2NΔφ)=E0αsinα⋅sinβsin(Nβ)
衍射光栅的光强分布
I=I0(αsinα)2⋅(sinβsin(Nβ))2
- 定义主极大 β=kπ,(sinβsin(Nβ))2=N2, 此时分子分母均为 0, 但极限不为 0, 且取到最大值, 可得主极大的位置
dsinθ=kλ(k=±0,1,2,…)
主极大位置与光栅缝数 N 无关, 只与光栅常数 d 有关
- 由于成像角度 θ∈(−π/2,π/2), 因此主极大的级数有限
- 定义极小 β=(k+Nm)π(m<N), 此时分子为 sinβsin(Nβ)=0, 分母不为 0, 因此光强为 0, 可得极小位置为
dsinθ=(k+Nm)λ(m=1,2,…,N−1)
- 定义次极大为两个极小之间的峰值, 通常比主极大小得多
- 根据极小定义, 当 m=0, 即主极大, 因此主极大相当于对将 θ 以 λ 划分, 极小相当于对 λ 再进行 N 等分, 一个 λ 中有 N−1 条分界线, 次极大位于每小段之间, 共 N−2 个 (两侧主极大各占一小格)
- 定义 k 级主极大半角宽, 即一小格的角宽度 (注意 sinθ 并非线性变化)
Δθk≈Ncosθkλ
因此随着缝数增多, 主极大 (亮条纹) 变窄
- 与双缝类似, 光栅衍射也存在缺级, 条件依然为 k=k′ad 可以此判断 ad 大小
非水平入射情况
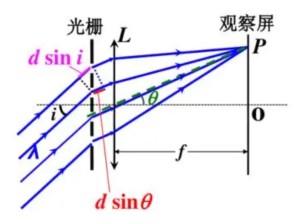
当平行光不是水平入射, 而是存在入射角 i=0, 则相当于入射前的光还存在一个额外的光程差, 此时光程差为
δ=d(sinθ+sini)
因此公式中
β=λπd(sinθ+sini)
光栅色散
使用复色光照射光栅, 除了中央主极大, 每个波长的主极大不重合, 且与中央主极大距离为 kλ, 可以此法计算复色光的光谱
角色散
为了确定光栅的辨色能力, 对于波长在 λ∈(λ,λ+dλ) 内, 相应主极大的距离 dθ, 定义角色散 (为了提高辨别度, 角色散越大越好)
D=dλdθ
为了求得 D, 对光栅主极大条件做微分可得
dcosθdθ=kdλ
因此, 对于 k 级主极大的角色散可表示为 (通常取 k=1,2, 否则光强过小)
Dk=dcosθkk
考虑成像与透镜的距离 f 后有
D∗=dλdx=fDk=dcosθkfk
光栅的辩色能力
定义光栅的辩色能力为
R=kN
其中 k 为主极大的级数, N 为光栅缝数
特殊衍射
X射线衍射
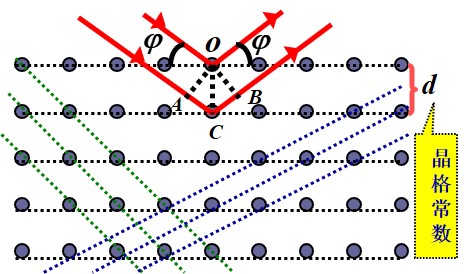
从 θ 处观察 (与水平晶面夹角), 当 X 射线的波长满足以下条件时, 干涉极大
λ=k2dsinφ(k=1,2,…)
圆孔衍射
当物体通过值径为 D 的圆孔成像时, 将产生衍射, 导致图像无法分辨, 定义
δφ=1.22Dλ
当两点与圆孔的夹角 θ>δφ, 认为两点可以分辨, 称 δφ 为仪器的分辨率
光的偏振
- 光波属于横波, 其电矢量 E 具有方向性
- 此处 E 不是相量, 而是电矢量, 垂直于光的传播方向
- 可以向正交方向分解电矢量为两列光波 Ex,Ey , 两列光波的电矢量垂直, 初相位不同, 振幅也不同, 但频率相同
偏振状态
线偏振光
当 Ex,Ey 的相位差 Δφ=0,π 两个分量的变化趋势完全相同, E 保持在固定的方向内, 矢量端点轨迹为直线
圆偏振光
当 Ex,Ey 的相位差 Δφ=±π/2, 振幅相同 E 以固定的角速度 ω 变换方向, 矢量端点轨迹为一个圆
椭圆偏振光
当 Ex,Ey 不满足以上两种条件 E 矢量端点轨迹为椭圆
自然光
当 Ex,Ey 的相位差无关联, 可能有任何取值, 且平均振幅相同, 则称为自然光
部分偏振光
当 Ex,Ey 的相位差无关联, 可能有任何取值, 但平均振幅不同, 且均大于零, 则称为部分偏振光
马吕斯定律
偏振片
- 能够吸收特定方向偏振光的薄片, 与之垂直的方向则能够完全通过, 称为偏振化方向
- 光线通过偏振偏后, 吸收方向的分量被吸收, 垂直方向的分量通过
- 无论何种状态的光, 透射后的光线必定为线偏振光
马吕斯定律
当强度为 I0 的线偏振光通过偏振片 (称为检偏器) 后, 假设偏振方向与偏振化方向的夹角为 α, 投射后的光强为
I=I0cos2α
布鲁斯特定律
- 当自然光入射到介质界面后, 反射光与折射光均为部分偏振光, 其中反射光的垂直于入射平面的光振动分量更强, 折射光相反
- 当入射角为 iB 时, 反射光与折射光垂直, 此时反射光为线偏振光, 但折射光仍为部分偏振光
- 根据折射定律, 假设入射光所在介质 n1, 可得
n1siniB=n2sin(π/2−iB)
因此
taniB=n1n2
双折射
晶体双折射现象
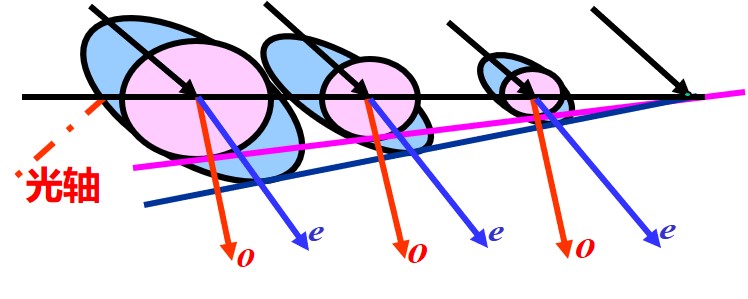
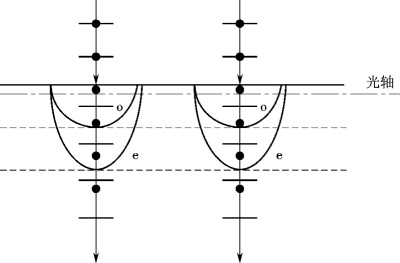
- 各向异性介质 (晶体) 中, 一束入射光将产生两束折射光, 将符合折射定律的折射光称为 o 光, 另一束则称为 e 光
- 晶体中存在一个方向, 沿此方向不发生双折射, 称为光轴 (存在无数条, 相互平行)
- 对于晶体中的点光源, 经过一段时间后, o 光产生普通的球面光, e 光则产生椭球面光, 且在光轴上于 o 光产生的球面相切 这是由于 e 光中, 光沿垂直于光轴的方向传播速度 ve=vo
- 当 vo>ve 称为正晶体, 球面在椭球面外 (此时 no<ne=vec)
- 当 vo<ve 称为负晶体, 球面在椭球面内 (此时 no>ne) 当入射面与光轴平行时, 产生的 o 光与 e 光的光振动垂直
波片
- 当入射光垂直于光轴, 产生的 o 光与 e 光的光振动垂直, 并且由于垂直波速不同, 当光线出射后重新叠加, 出射光的光振动关于 e,o 方向的分量相位被改变, 根据此原理制成波片
- 波片厚度 d 满足 Δφ=λ2π(ne−no)d, 只对特定的 λ 有效
- 对于自然光, 波片无法改变其状态
四分之一波片
- 能够产生 π/2 的相位差
- 当入射光为线偏振光
- 当与 o 光或 e 光的光振动方向相同, 则出射仍为线偏振光
- 当与 o 光或 e 光的光振动夹角为 45∘, 则初射后, 正交分量振幅相同, 相位差 π/2, 为圆偏振光
- 其他情况下, 由于正交分量振幅不同, 为椭圆偏振光
- 当入射光为圆偏振光, 圆偏振光向任意方向分解, 相位差均为 π/2, 再次改变后, 变为 π, 因此变为线偏振光
- 当入射光为椭圆偏振光, 如果其 o 光与 e 光的分量为 π/2 (主轴), 则出射线偏振光, 否则仍为椭圆偏振光
半波片
- 能够产生 π 的相位差
- 入射光为线偏振光时, 能够改变其偏振方向
- 入射光为圆偏振光时, 能够改变其旋转方向
偏振光的干涉
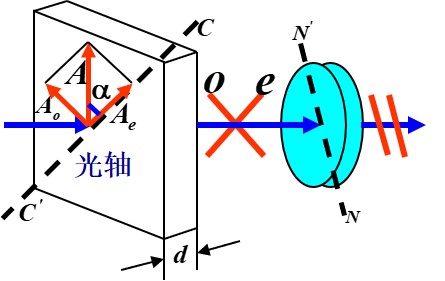
- 线偏振光通过波片, 改变其 o 光与 e 光方向分量的相位差
- 再通过偏振片, 获得其 o 光与 e 光方向分量在偏振片方向的投影
- 此时可将 o 光与 e 光方向分量视为两束叠加的相干光
- 两束光有相位差, 只与入射光波长与波片厚度有关 (只考虑相位差, 不考虑振幅大小)
Δφ=λ2π(ne−ne)d
- 如果投影后, o 光与 e 光方向相反, 则要附加光程差 π/2, 此时转动偏振片, 可能使其投影后方向相同, 导致干涉结果变化
















