解题注意

易错总结

切应变负号含义

1. 对于 $\tau_{ab}$, $a$ 表示微面方向, $b$ 表示切应力方向
2. 在莫尔圆中 $\sigma_x$ 与 $\tau_{xy}$ 表示一个点

莫尔圆与实际值的转换

实际值为莫尔圆周上的点, 需要注意

1. 圆心的位置
2. 莫尔圆上的旋转角为方位角 $\alpha$ 的两倍
3. 莫尔圆上的 $\sigma$ 轴对应的是主方向, 还需要旋0转 $-\alpha_0$ 得到 $x$ 轴对应的方向

$$\sigma_{\alpha=\theta}=\sigma_c+R\cos[2(\theta-\alpha_0)]$$

应力与应变的关系

• 应力与应变的转换需要考虑泊松效应

$$\varepsilon_{\alpha}=\frac{\sigma_{\alpha}}{E}-\mu\frac{\sigma_{\alpha+90^\circ}}{E}$$

• 某个方向上应力为 $0$, 应变不一定为 $0$

弯曲剪应力

可求出 / 无说明不要求时, 需要计算 (如已知应变求力), 但通常在危险点 (外表面) 上为 $0$

$$\tau=\frac{F_s S^*_z}{bI_z}$$

最大弯曲剪应力

• 梁的最大弯曲剪应力点必定在截面的形心上 (中性轴)
• 对于矩形截面梁

$$\tau_{max}=1.5 \frac{F_s}{A}$$

• 对于圆截面梁

$$\tau_{max}=\frac{4}{3} \frac{F_s}{A}$$

柔度判断

柔度越大, 压感的极限应力越小, 大柔度杆为 $\lambda>\lambda_p$

杆件受力分析

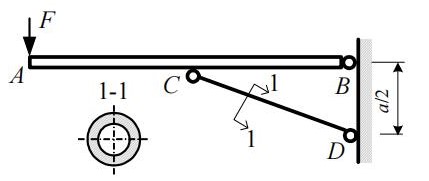
1. 对于仅受两个力的杆件 (任意刚体), 即可视为二力杆, 二力杆仅受拉或受压 (通常用于稳定性分析), 通过引入二力杆以简化受力分析过程
2. 如图中杆 $CD$ 上仅有两个约束力, 因此为二力杆; 杆 $AB$ 上除约束力外还有一个外力, 因此为一般杆件
3. 因此铰链 $B$ 具有两个方向的约束力, 而 $D$ 上的约束力沿杆件方向, 仅需对 $B$ 点取矩即可求出 $CD$ 杆的压力
4. 在刚体受力分析中, 通过对不重要的力所在直线上的点取矩, 避开求此力
5. 对斜方向的力求矩时, 最好将力正交分解为两个力分别求矩, 便于求力臂

弯矩图方向

当采用一般方法判断弯矩正方向后, 弯矩图的正值应画在钢架内侧

虚拟力系

1. 在相对移动 / 相对静不定问题中, 添加的虚拟力应为一对在相对点上的力系, 力 (力偶) 方向对称, 大小相同
2. 当采用受拉为正时, 截断桁架产生的约束力方向应与截面法向相同

弯矩分析

1. 存在集中弯矩时, 此处的弯矩将会突变, 不能遗漏
2. 对于铰链杆, 注意集中弯矩在铰链的哪一侧, 集中弯矩的位置对结果有影响
3. 对直杆上的点也可视为钢架的拐角点分析, 从而重置坐标系便于积分
4. 拐角点分析中, 必须将所有被分析过的部分的外力移到拐角点上再继续分析, 并且拐角点上的弯矩在左右连续 (集中弯矩除外) , 并将已分析部分的弯矩在新的分析部分中作为常数
5. 通过检查各段弯矩是否连续, 在集中弯矩处是否突变, 最后取值是否为 $0$ (最后有固定约束时不一定), 确定弯矩是否正确

自由度判断

1. 定义物件总数 $N$, 包括机架 (当不存在与机架连接的约束时则不包含)
2. 一般铰链为低副, 滑动铰链为高副, 固定端约束则取 $3$, 注意多重铰链
3. 自由度满足 $FoD=3N-3-C$, $C$ 为被约束的自由度总数, 当 $FoD<0$, 为超静定结构

直径与半径

1. 求 $I_z,I_\rho$ 公式中, 带入直径
2. 求面积时, 如果使用直径计算, 则需要乘 $\frac{1}{4}$, 且直径增加两倍厚度
3. 求弯曲应力中的 $y$ 为到中性轴的距离, 因此为 $D/2$ 或 $h/2$
4. 求偏心压缩的弯矩 (斜齿轮) 或扭矩时, 力臂长度一般为半径