基本变形
大约 19 分钟
基本变形
内力分析
截面法
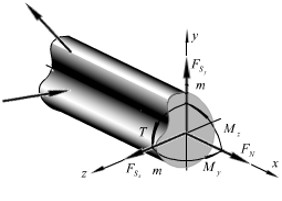
刚体中的力或力偶可移性原理不适用于变形体, 为了研究变形体, 对变形体取截面研究截面的内力
截面法过程
- 对变形体取一个任意截面, 使变形体分为两个部分并取任意一个部分研究
- 规定截面上内力与内力矩集中于截面的形心, 并以截面指向研究部分外的法线为 轴正方向, 截面形心为原点, 建立右手坐标系
- 由于物体静止, 因此截面上的内力及内力矩与研究部分上的外力平衡, 即合力为
- 计算内力时注意
- 截面内力与外力平衡, 不是等于外力合力, 有
- 计算内力时可以将研究部分视为刚体, 并且使用力平移定律与力矩平移定律 (力平移后, 将产生一个力矩, 其力臂为平移后点指向平移前点)
- 对于不过形心的轴力, 将产生两个扭矩 (非对心压损 / 斜齿轮接触点轴向力)
- 注意截面形心坐标系的 轴方向为截面向外的法线, 当截面方向不同时, 坐标系不同
- 截面可以任取, 但只能有一个 (薄壁圆桶问题中两个截面实际在同一个平面上)
- 对于同一个截面, 取不同的研究部分, 结果不一定相同
- 根据内力计算得到各个位置截面内力的函数, 并画出内力图
截面内力的正方向
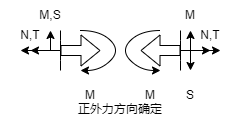
- 对于截面内力
- 轴力, 扭矩的正方向与截面法线方向重合
- 在纸面 ( 面) 内, 使梁段产生顺时针转动的剪力为正 (截面法线顺时针旋转 到达剪力正方向)
- 在纸面 ( 面) 内, 使梁段产生向内 轴负方向弯曲的弯矩为正 ( 轴正方向一侧梁受压, 因此此时的弯矩图 轴向下)
- 已知分析方向时, 产生正内力的外力方向
- 轴力, 扭矩的正外力与分析方向相反
- 剪力的正外力为分析方向逆时针旋转 得到
- 产生正弯矩的 正外剪力 为杆件向外的方向 (对于水平杆即 轴方向)
- 产生正弯矩的 正外弯矩 的旋向箭头与正外剪力相反, 弧线包裹分析方向
内力图画法
- 确定截面形心位置与主轴方向 (对于弯曲变形特别注意)
- 将各个位置的力集中到轴线上, 并按照三个坐标轴方向分解
- 对于轴线外的力则平移到轴线上, 并产生一个力矩
- 对于斜方向的力, 需要向坐标轴投影
- 对于一个截面上的多个力, 可能产生的扭矩相互抵消, 但剪力效果相互叠加, 要具体分析
- 确定约束力 (对于单个约束如固定端约束, 可作为最后分析点, 从而避免求约束力)
- 确定内力的分析方向, 截取截面沿此方向移动, 同时也是截面的 轴正方向
- 根据分析方向确定在此参考方向上, 产生正内力的外力方向, 便于分析
- 沿分析方向, 从截面一端分析至另一端, 从 开始, 经过存在外力的截面时, 内力根据界面的值发生突变
- 分析完成后, 轴两侧的内力必定为
- 对于弯矩图与剪力图, 还具有以下特点
- 弯矩与剪力存在积分关系, 即 因此可先求出剪力, 并由剪力积分得到弯矩
- 此积分关系无法反应集中弯矩, 需要具体求解
- 对于复杂的弯矩情况, 可通过叠加法求解, 即仅求出各个外力单独作用下的弯矩, 最后再进行叠加
- 为了是梁受拉部分在坐标轴上方, 规定弯矩图中, 竖轴正方向朝下
特殊内力图
- 钢架内力图
- 将钢架拆分为独立杆件分别分析
- 在杆的交点, 需要将钢架在角点截开, 然后将没有被分析杆部分视为刚体然后将其外力 (包括约束力) 全部移动到交点上 (移动力可能产生附加力矩)
- 在分析各个杆的时候仍需要规定好分析方向
- 在画钢架内力图时, 要求弯矩出现在受拉一侧 (有弯矩曲线的一侧受拉), 当采用一般正方向时, 弯矩的正值在钢架内侧
- 交点处的力对于一侧的杆为剪力, 对于另一侧的杆可能为轴力
- 钢架内约束特点
- 钢架内的铰链约束
- 需要先求出约束力再进行分析
- 由于铰链约束上无约束力矩, 因此内力图在铰链约束处的弯矩为
- 钢架内的转角
- 需要通过截面法截开转角, 将其它力平移到转角上分析
- 由于力偶无方向性, 因此转角处的力偶在两个杆之间连续
- 钢架内的铰链约束
- 弧形钢架
内力图快速画法
通过叠加法实现内力图的快速画法
- 即在每个受力状态变化点后使函数叠加上该点的变化 (可能一次叠加多个力)
- 叠加只对之后的值有效果, 对之前的值无效, 因此要分段
- 通过 改变坐标系, 从而使用 时力单独作用的结论
- 需要先计算得到约束力才能开始
一般内力图
- 用于扭矩, 轴力与剪力
- 内力在集中力点上突变, 即在 该点后 函数叠加常数
- 对于分布力系, 则为 该点后 函数叠加 , 为分布力开始位置, 分布力系结束后, 将其在结束点之后的值视为常数, 常数大小为结束点上的叠加效果
弯矩内力图
- 根据 , 在剪力处, 该点后 函数叠加
- 对于分布剪力系, 则为叠加 , 结束后处理相同
- 对于集中弯矩则直接叠加常数
钢架内力图
- 此结论仅在使用相同规则的弯矩正方向并且按一个分析方向走完整个钢架时成立 (以钢架向外为正)
- 由于弯矩在拐角处弯矩连续的特点, 因此在下一根杆上开始时的弯矩叠加上常数, 等于上一根杆在此处的弯矩
- 通过此方法避免求外力移动产生的矩 (相等), 仅需将外力移动到弯折点即可 (注意方向转变使力的性质转变)
内力作用效果
| 符号 | 名称 | 方向 | 变形效果(能量角度) |
|---|---|---|---|
| 轴力 | 方向的力, 垂直于截面 | 伸长量 | |
| 剪力 | 方向的力, 平行于截面 | 挠度 | |
| 扭矩 | 方向的转矩, 产生扭转变形 | 扭转角 | |
| 弯矩 | 方向的转矩, 产生弯曲变形 | 转角 |
轴向拉压
拉压正应变的计算
取轴上的微段 , 在拉力的作用下发生了变形, 长度变为 , 定义轴向线应变为 (注意不是变化前后长度之比, 而是长度变化量与原长之比)
拉压正应力的计算
认为轴向的正应力在垂直于轴线的轴截面 (横截面) 上均匀分布, 因此横截面上正应力的合力即截面上的轴力 (属于内力, 不是外力) 满足
拉压变形的计算
- 根据胡克定律可得, 在材料的线弹性阶段, 拉压变形物体的应变与应力成正比, 满足
- 根据应变与应力的关系可得拉压伸长变形满足
- 积分可得到拉伸变形量与轴向内力 满足关系
其中 为截面轴力关于截面位置的函数, 定义 为拉压刚度
其他有关问题
横向变形
有关横向变形与泊松比部分见应力状态
拉压超静定问题
扭转变形
扭转切应变的定义
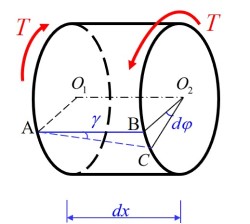
- 取微段 , 微段端面上有两点 , 在经过扭转变形后, 点变形至 点, 定义切应变为 变形的角度
- 根据切应变定义可得扭转切应变表达式为, 可得切应变的大小还与截面上点的径向位置 有关 (几何条件)
扭转应力的计算
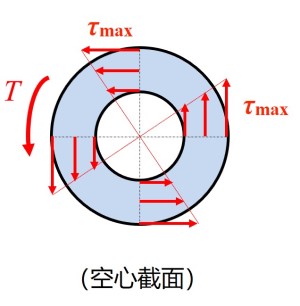
- 根据胡克定律可得, 应力与应变满足关系
- 扭转变形中, 切应力的合力即截面上的扭矩 (属于内力, 不是外力), 因此可得到切应力满足 (物理条件)
- 其中 为极惯性矩, 为一个与截面形状有关的物理量, 其定义为
- 对于厚圆筒截面满足
- 可得, 在圆柱的表面切应力达到最大, 最能反映圆柱面强度, 因此定义抗扭截面系数 , 单位为
扭转变形的计算
- 根据切应力的表达式与胡克定律可得扭转变形中, 微段 的扭转角 满足
- 积分可得到扭转变形的扭转角
其中 为截面扭矩关于截面位置的函数, 定义 为扭转刚度
- 定义单位长度的扭转角 , 反应任意截面的扭转变形强度, 满足
弯曲变形
在本节讨论中, 做出以下定义
- 定义 轴为梁的轴线, 弯曲变形发生在 截面, 截面几何量均相对于 截面讨论
- 定义 轴正方向为梁受拉侧指向受压侧的方向, 即弯曲方向
- 定义 轴为梁的中性轴, 即平行且通过梁中性层的轴线 (梁中未发生拉伸变形层, 同时也是受压与受拉的分界层), 同时弯矩也为 轴方向
- 公式在其他截面情况下依然成立, 但弯曲方向与中性轴需满足右手定则, 否则要取负号
纯弯曲正应变的计算
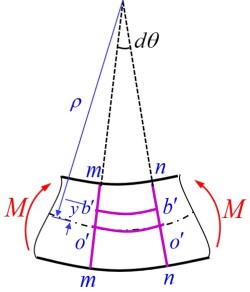
- 纯弯曲中, 梁仅受弯矩作用, 没有剪力, 因此梁上仅有正应力, 没有剪应力, 每个截面均匀绕中性轴偏转, 梁弯曲成为一条圆弧线
- 对变形后的圆弧取一个段 , 由于中性层不变的性质有 , 其中 为弯曲微段的曲率半径, 根据线应变的定义可得, 线应变满足
纯弯曲正应力的计算
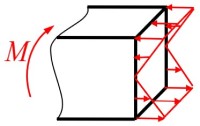
- 根据胡克定律将应变转为应力, 并且带入物理条件截面上应力的合力矩与弯矩相同, 且合力为 (截面上没有轴力)
- 根据截面无轴力条件可得, 中性轴上满足条件 , 即中性轴 位于截面关于 轴的形心上 ( 为截面静矩)
- 根据截面上应力的合力矩与弯矩相同可得, 弯曲正应力与弯矩满足关系
- 其中 为截面相对于 轴的惯性矩 (相对于 的距离即 坐标), 单位为 , 具体计算见后
弯曲剪应力的计算
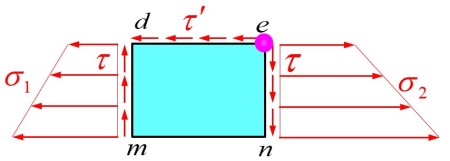
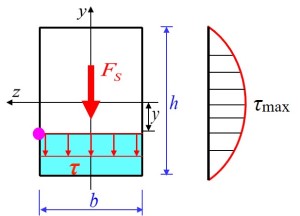
- 一般弯曲中, 由于剪力的存在, 因此弯曲变形还存在剪应力与剪切变形 (变形效果为使梁不均匀弯曲或上下面错位), 但通常极小, 可忽略, 并假设弯曲截面上的剪力均平行于剪力 (不均匀分布)
- 先取微段 (即图中的 ), 再对微段 处取截面
- 由于受剪力时, 弯矩不为常数, 因此微段两侧的正应力合力为 (注意弯矩与剪力的微分关系), 因此截面上也将存在切应力, 并且使微段的轴向力为
- 根据切应力互等原理, 下表面无切应力并且两侧面与截面的交界处切应力与截面互等 (不是整个侧面), 由此可得弯曲切应力满足
其中 为截面 轴方向的宽度, 为被截微段的侧面相对于 轴的静矩
- 可得剪应力的分布特点为两侧为 , 中性轴上剪应力最大
- 对于矩形截面,
- 对于圆截面,
弯曲变形的计算
- 联立弯曲正应变与弯曲正应力可得
- 注意在小变形条件下将 近似为微圆弧段, 有关系
- 定义 为弯曲梁的挠度函数, 为弯曲梁的转角方程, 其与曲率半径满足关系 , 因此有二次微分方程
可通过线积分得到梁的挠度与转角
- 积分时将产生未知的积分常数 (挠度两个, 转角一个), 为了解出积分常数, 需要根据约束带入边界条件
- 处有固定端约束则
- 处有铰链约束则 (通常有两个且非 处的常数通常不为 )
- 处两梁连续则 (对于弯矩不连续 / 界面变化处必须将梁分为两段处理)
刚化叠加法
- 刚化叠加法为将复杂结构分段, 将每一段视为弹性体其他视为刚体分别分析, 最后叠加
- 通常根据受力分段, 在集中力处分段, 在分布力作为一段等, 使之与简单情况相同便于分析
- 对于刚体满足以下性质
- 刚体上的力或力偶可以任意移动至刚体与弹性体的交界 (可能产生附加力矩)
- 刚体上 , 但与弹性体交界处仍满足约束的边界条件 (见上)
- 刚体与弹性体接触时的受力可认为有垂直于接触方向的约束力
- 对于远离弹性体确认不会变形的刚体可以不分析
有关截面几何量的计算
静矩计算
- 静矩定义
- 静矩与形心坐标满足关系
其中 为形心 坐标 (可能有正负), 为图形面距
可根据此公式计算界面静矩, 静矩除以截面面积得到形心位置
在截面的对称轴上静矩为
- 静矩可直接叠加 / 相减, 因此对于复杂图形可通过简单图形静矩的组合或去除得到截面静矩
- 矩形的形心位置即长宽中点的交点
惯性矩计算
- 惯性矩定义
- 在求出形心位置即 轴坐标后再求截面惯性矩
- 对于常见图形形心在原点上的惯性矩有
- 圆筒
- 矩形 为 轴方向的高度
- 对于形心不在原点的图形, 可通过平行移轴定律计算惯性矩
其中 为图形面积, 为图形形心的 坐标
- 惯性矩可以进行叠加, 因此对于复杂图形可通过简单图形惯性矩矩的组合或去除得到截面惯性矩
弯矩面坐标轴的选择
- 以上的弯曲公式仅在以下条件下成立
- 选择截面的形心主惯性轴作为坐标系 (查看题目要求, 用于非对称截面)
- 将截面的对称轴作为 或 轴, 且另一轴过形心 (根据此要求, 矩形只能以两个对称轴作为 轴, 圆形则可任意选择)
- 为了使用弯曲公式, 分析弯矩时, 必须采用以上要求的坐标轴
- 注意当中性轴为 轴, 弯曲方向为 轴时, 右手关系不满足, 因此公式需要取负号 (原来负号被抵消)
- 对于不平行于坐标轴的剪力或弯矩, 需要分解投影到坐标轴上分别计算变形
- 计算两个方向的变形时, 注意坐标轴两个方向上的惯性矩不同
- 求总挠度时, 可以使用平行四边形法则将两个方向上的挠度叠加
复合梁的弯曲变形
- 复合梁为截面上由两种材料组成的梁, 两种材料弹性模量与形状不同
- 对于复合梁, 其应变连续但应力不连续, 需要对弯曲公式进行修改
- 通过等效截面法计算 轴的位置 (不是形心)
- 复合梁中性轴满足条件
- 选择其中一种材料 为基础, 另一种材料在 轴方向长度变化 , 得到等效截面
- 计算等效截面的形心即 轴位置
- 梁的应变连续, 因此复合梁的刚度为 , 但应力不连续, 依然通过虎克定律求出有
其中 为材料 部分的惯性矩 (相对于原始截面)
偏心拉伸与压缩
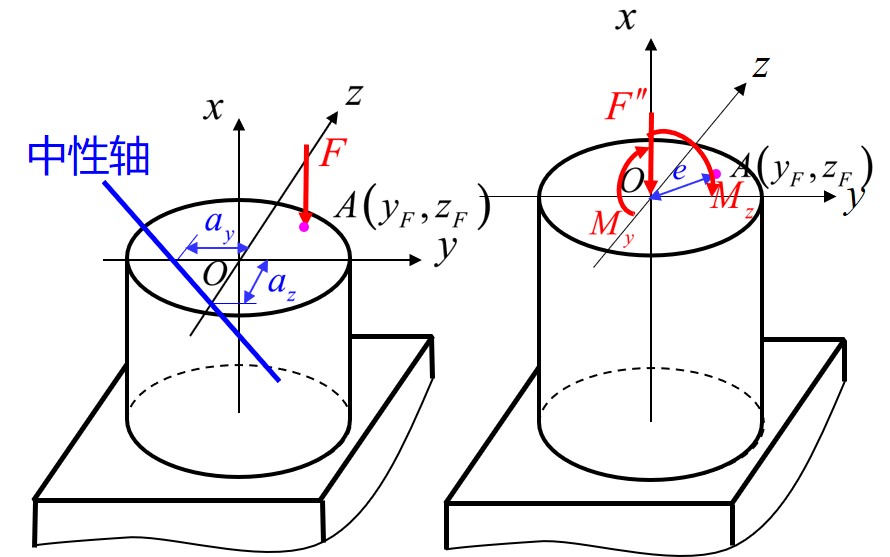
- 当轴力 (内力) 不过截面形心时, 需要将其平移至截面形心处, 同时对 轴产生弯矩, 因此截面将沿 方向发生弯曲变形 (注意弯曲公式的符号)
- 截面的应力将由均匀分布的拉伸应力与两个弯曲应力叠加而成, 定义截面上拉应力与压应力的交界线为中性轴 (正应力为 ), 因此可得中性轴满足 (提出 与 )
设中心轴所在点的坐标为 , 偏心压力作用点为
- 由中心轴条件可得, 当偏心压力坐标越大, 中性轴越靠近形心
- 为了保证截面仅受压应力 (脆性材料), 需要保证在最偏心的压力作用下, 中性轴仅与截面相切, 这个偏心压力作用范围称为截面核心
- 计算截面核心时, 可假设中心轴过截面最外侧交点, 并带入 , 得到一条截面核心的边界线
- 对于圆形截面, 截面核心为圆, 带入圆边缘一点即可得到其半径
- 对于矩形截面等多边形, 危险点为多边形的顶点, 叠加各个顶点对应的边界线即可得到截面核心
- 在校核截面是否受拉应力时, 危险点位置与上同
- 为了保证截面仅受压应力 (脆性材料), 需要保证在最偏心的压力作用下, 中性轴仅与截面相切, 这个偏心压力作用范围称为截面核心
材料力学性能
低碳钢力学性能
低碳钢拉伸
| 符号 | 阶段 | 符号含义 |
|---|---|---|
| 线弹性 | 线弹性阶段的极限应力 (proportion limit) | |
| 非线性弹性 (胡克定律不成立) | 弹性阶段的极限应力 (elastic limit) | |
| 屈服阶段 (同时存在塑性与弹性变形) | 材料于屈服阶段的最低应力 (yield strength) | |
| 强化阶段 | 材料在强化阶段的极限应力, 超过此应力后开始颈缩阶段, 材料断裂 (breakdown) |
低碳钢压缩
低碳钢压缩时将不断变形, 不存在断裂, 仍有屈服与强化阶段
铸铁力学性能
铸铁拉伸
不存咋屈服阶段与颈缩断裂现象, 断裂时形变很小, 仅有断裂时应力为极限应力 作为强度指标
铸铁压缩
铸铁的压缩强度为铸铁的拉伸强度的 倍, 断裂口的方位角为 , 也仅有断裂时应力为极限应力 作为强度指标 (铸铁拉伸与压缩下极限应力不同)
安全系数
- 定义材料的极限 (ultimate) 应力 为材料失效时的应力
- 其中, 低碳钢采用屈服强度 , 铸铁采用抗拉(压)极限 作为极限应力
- 定义安全系数 , 并有许用应力
- 要求设计结构后必须对其危险截面 (内力大 / 截面刚度小) 进行许用应力的校核