能量法

克拉贝隆原理

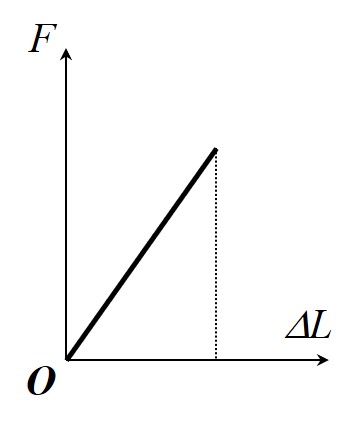
• 定义应变能 $U$ 为物体发生应变后的内能, 根据能量守恒其值等于外力使物体变形时在物体上的做功 $W=\int F(\delta)d\delta$, 其中 $\delta$ 为外力的位移, 同时也是物体的变形量
• 对于线弹性材料, 外力大小与形变量成正比, 有 $F(\delta)=k\delta$, 因此曲线 $F(\delta)$ 与坐标轴围成一个直角三角形
• 定义 $F$ 为平衡状态下的外力, 满足 $F=k\delta$, 因此, 对于任意个外力 $F_i$ 以及其产生的形变 $\delta_i$, 应变能满足

$$U=W=\sum_{i=1}^n\frac{1}{2}F_i\delta_i$$

应变能计算

1. 克拉贝隆原理中, 需要分别求出外力与形变量, 不方便使用
2. 通过截面法截取微段 $dx$ , 微段截面上的内力即对微段的外力, 微段的形变量也仅与微段所受的外力有关, 对微段的应变能积分即可得到物体的应变能, 且应变能的结果仅与内力有关
3. 由于弯曲切应力的应变能为其他应变能的高阶无穷小, 因此在能量法中一般不讨论弯曲切应力

基本变形的应变能

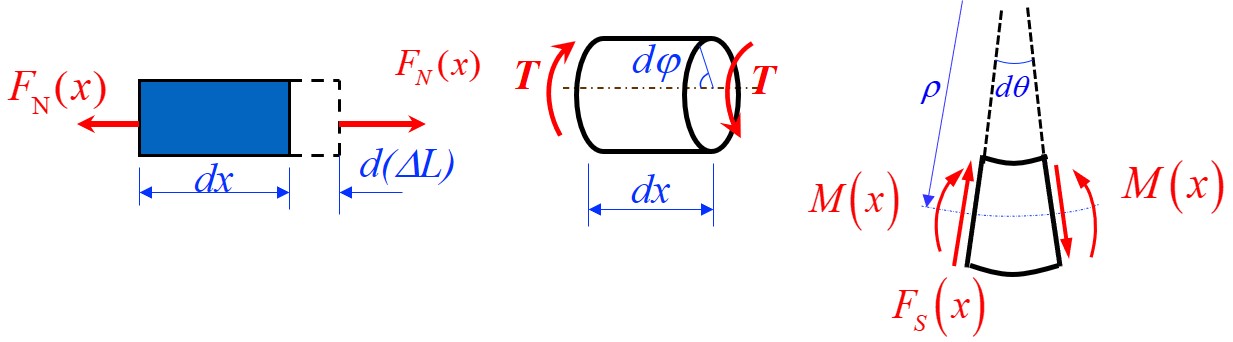
• 拉压变形

$$U=\int_L\frac{1}{2}\frac{F_N^2dL}{EA}$$

• 扭转变形

$$U=\int_L\frac{1}{2}\frac{T^2dL}{GI_\rho}$$

• 弯曲变形

$$U=\int_L\frac{1}{2}\frac{M^2dL}{EI}$$

组合变形的应变能

1. 由于应变能为内力的二次关系, 因此一般情况下应变能不可叠加
   • 注意此处叠加是指叠加由各个力产生的内力计算得到的应变能, 相当于 $\int\sum kF_{Ni}^2$
   • 但将各个力产生的内力先叠加得到总内力, 再计算应变能是允许的 (内力可由外力叠加得到), 相当于 $\int(\sum kF_{Ni})^2$, 两式显然不同
2. 对于不同类型内力产生的应变能 ($y,z$ 方向的弯曲变形也属于不同类型), 不考虑剪力时, 认为之间的变形不耦合, 因此可以进行叠加

$$U=\int_L\frac{1}{2}\frac{F_N^2dL}{EA}+\int_L\frac{1}{2}\frac{T^2dL}{GI_\rho}+\int_L\frac{1}{2}\frac{M^2dL}{EI}$$

应变能积分

• 对于一般钢架与轴, 在具体分析各段杆的内力后, 可使用杆上点的坐标表示各个微段, 并求出内力函数, 但注意积分方向必须与截面移动方向, 截面法向相同, 此时有 (以 $x$ 坐标为例, 假设仅有弯矩)

$$U=\int_0^l\frac{1}{2}\frac{M(x)^2dx}{EI}$$

• 对于圆弧形杆件
  • 可采用角度坐标表示内力, eg $M(\theta)$
  • 积分时需要有坐标变换 $dL=rd\theta$, 且积分方向与分析方向要一致
  • 由于圆弧上微段的法线方向不固定, 因此截面坐标轴轴方向也不固定, 其中 $y,z$ 始终平行于截面, $x$ 始终垂直于截面, 求内力时要注意不同角度下轴的方向

卡氏定律

• 在力 $F_i$ 作用下, 物体发生形变 $\delta_i$, 对于物体的总应变能 $U$, 形变满足 (假设仅有弯矩)

$$\delta_i=\frac{\partial U}{\partial F_i}=\int_0^l\frac{\partial M}{\partial F_i}\cdot\frac{M(x)}{EI}dx$$

• 公式中积分计算与偏导计算无先后顺序, 一般先求偏导再积分
• 集中力 $F$ 对应的位移是直线位移 $\Delta x$, 集中力偶对应的位移是角位移 (转角) $\theta$, 其中位移的正方向与力的方向相同

虚拟力法求任意方向的形变

• 如果要求结构上任意一点的位移, 并且位移与外力无关时, 可在结构上添加一个虚拟力, 然后令结果中的虚拟力为 $0$ 即可

$$\Delta=\frac{\partial U}{\partial F'}\bigg|_{F'=0}=\int_0^l\frac{\partial M}{\partial F'}\bigg|_{F'=0}\cdot\frac{M(x)\bigg|_{F'=0}}{EI}dx$$

• 在求出偏导后, 即可令 $F'=0$, 再进行积分, 简化积分运算
• 求相对位移时, 则需要在两个相对点添加一对对称的力系 (力偶系), 并单独分析力系的影响分析时, 从一个点分析至另一个点, 仍要考虑约束

解题过程

1. 添加虚拟力 (如果所求点位移不能由外力直接求出)
2. 确定各根杆的分析方向 (一般从无约束段开始, 对同一根杆上的各个力必须统一)
3. 根据题目要求与受力分别求出各个外力作用下的内力 (使用叠加法便于分析) $F_{Ni}(x),T_i(x),M_i(x)$
   1. 弯曲钢架一般不考虑 $F_N$
   2. 无扭转变形时不考虑 $T$
   3. 剪力不考虑
4. 对要求位移的部分求偏导 $\frac{\partial M_i}{\partial F_i},\frac{\partial T_i}{\partial F_i},\frac{\partial F_{Ni}}{\partial F_i}$ (如果不包含 $F_i$, 则偏导结果即为 $0$, 可不考虑)
5. 将 $F'=0$ 带入偏导与内力结果中
6. 先对内力与偏导结果分别叠加, 再积分得到位移 (假设仅有弯矩)

$$\Delta=\int_0^l\sum_{i=1}^n\frac{\partial M_i}{\partial F'}\bigg|_{F'=0}\cdot\frac{\sum_{i=1}^nM_i(x)\bigg|_{F'=0}}{EI}dx$$

平衡力系作用下的形变

在没有约束的平衡力系中, 求出的形变是物体的相对形变, 因此可将其中一个或几个与位移无关的力视为固定约束, 求出的形变即相对这些力的形变

互等定律

• 定义位移 $\delta_{ij}$, $i$ 表示位移方向与位置与 $F_i$ 相同, $j$ 表示位移在 $F_j$ 作用下产生
• 对于两个不同力系对同一个物体作用下, 有 (同方向的位移与力相乘才有意义)

$$F_1\delta_{12}=F_2\delta_{21}$$

• 当两个力系共同作用时, 则实际位移为 $\Delta_1=\delta_{11}+\delta_{12}$
• 可通过互等定律转化对特定位置位移的求解 (转化为一个作用在目标位置的虚拟力, 求其在实际力作用位置产生的位移)

超静定问题

1. 超静定问题中首先判断超静定的次数 $n$, 然后去除 $n$ 个多余约束, 将其转变为未知约束力
   • 根据自由度分析超静定次数, $n=-FoD=3+2P_L+P_H-3N$ ($N$ 为物件数, 如果有与机架相连的部分则要包含机架)
   • 对于无固定约束的机构, 则 $N$ 即为物件数
   • 对于固定约束连接的几个物体认为是同一个
2. 分析外力与约束力 (包括未知与已知) 得到内力 (物理方程)
3. 去除约束得到的未知力依然满足约束效果, 即未知约束力的位移 $\delta=0$ (几何协调条件)
4. 由于超静定问题中几何协调条件的特点, 可使用力法正则方程表示几何协调条件
5. 对于问题中的刚体, 其应变能为 $0$, 因此可不分析刚体的内力与应变能 (但刚体对弹性体的影响仍要考虑)

力法正则方程

• 三种基本变形的静不定问题均可用力法正则方程, 且相互之间不耦合, 此处以弯曲变形为例
• 超静定问题中, 通常以约束力为待求量, 因此使用 $X_i$ 表示未知约束力
• 将未知力从其产生的内力中提出, 得到 $\overline{M_{Xi}}=X_iM_{Xi}$, 根据卡氏定律, 对于集中力与集中力偶 $\frac{\partial M_{Xi}}{\partial X}=\overline{M_{Xi}}$
• 定义柔度系数

$$\delta_{ij}=\int_L\frac{\overline{M_{Xi}}\cdot\overline{M_{Xj}}dL}{EI}$$

其中 $\delta_{ij}=\delta_{ji}$

• 根据卡氏定理即可得到力 $F$ 在 $i$ 处产生的位移效果 (不是实际位移) 与 $i$ 处的总位移满足

$$\Delta_{iF}=\int_L\frac{\overline{M_{Xi}}\cdot M_F}{EI}\;,\Delta_i=\sum_{j=1}^n\delta_{ij}X_j+\Delta_{iF}=0$$

• 整理几何协调条件即可得到力法正则方程 ($F_m$ 为外力系)

$$[\delta_{ij}]_{n\times n}[X_j]_n=\{-\sum_{m=1}\Delta_{iF_m}\}_n$$

• 对于多个外力, 也可分别分析再使用叠加法求出 $\sum_{m=1}\Delta_{iF_m}$
• 求出未知约束力 $X_i$ 后可带入得到实际截面弯矩 $M$ , 用于通过卡氏定理求解某个点的形变
• 注意内力图等可能会分成多段, 每一段都要计算

桁架静不定

• 由于桁架中的杆为二力杆, 因此各杆仅受轴向力且为常数 (与截面位置无关)
• 桁架受力分析方法与理论力学相同, 依然采用截面法, 并且以受拉为正 (受力与截面法线同向)
• 通过将杆件截断以去除约束, 截断的两个截面存在大小相同的拉力 (注意此拉力为内力, 因此应与截面法线同向), 对应的几何约束为两个截断面之间的距离保持为 $0$
• 注意杆虽然截断, 但其长度不变, 计算时必须考虑截断杆的应变能
• 在单独分析中, 截断杆的内力即未知约束力, 因此分析其他力时, 可将杆视为不存在; 但未知约束力对其他杆的内力要分析
• 同样最后可通过力法正则方程求解, 此时 (对每一根杆的内力都要计算)

$$\delta_{ij}=\sum^n_{k=1}\int_{L_k} \frac{\overline{F_{Ni}}\cdot \overline{F_{Nj}}dL}{EA}$$

• 桁架静不定中, 注意每一根杆的内力都要包括在内, 并且杆的长度不一定相同

对称结构的静不定

对称性条件

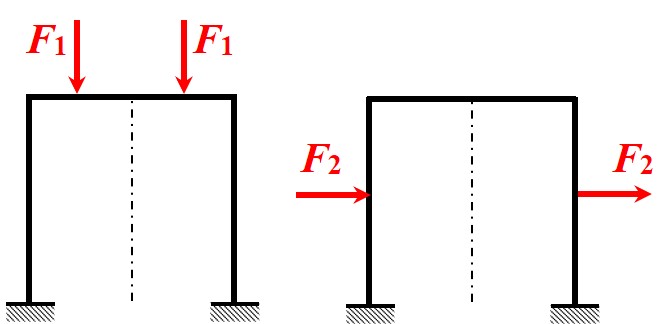
1. 对称结构 结构在对称轴两侧完全重合, 这是使用对称性的前提
2. 正对称载荷 结构上的载荷在沿对称轴对折后, 载荷的方向重合 (载荷的方向与作用点沿对称轴对称)
3. 反对称载荷 结构上的载荷在沿对称轴对折后, 载荷的方向相反 (载荷的作用点沿对称轴对称, 但作用方向相反)

对称轴上内力的特点

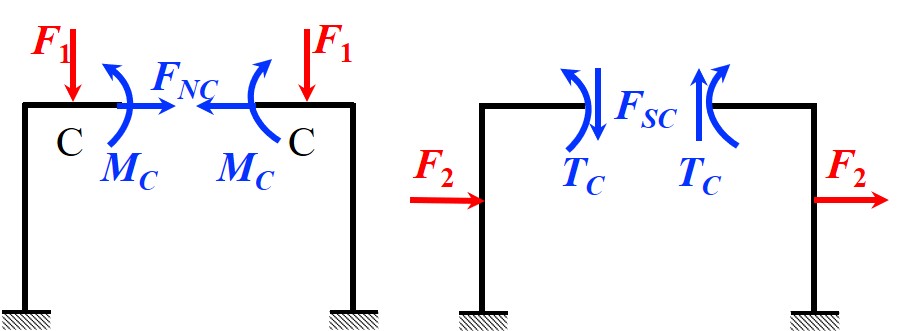
沿对称轴截开结构 (当对称轴上有杆件时, 可沿对称轴向左 / 右截, 并包含杆件), 其截面上的内力以及对称轴上微段的形变将满足以下特点

1. 正对称载荷
   1. 截面内力 $F_S=0,\;T=0,\;M_+=M_-,\;F_{N+}=F_{N-}$
   2. 形变特点 $x=\theta=0$
   3. 等效约束力 (低副) $M,\;F_{N}$
2. 反对称载荷
   1. 截面内力 $T_+=T_-,\;F_{S+}=F_{S-},\;F_N=0,\;M=0$
   2. 形变特点 $y=\varphi=0$
   3. 等效约束力 (低副) $T,\;F_{S}$
3. 钢架内的铰链 可沿过铰链的截面截开钢架, 并将钢架内的铰链视为一种特殊的对称点处理 (通常与另外两种对称点叠加, 再次简化)
   1. 形变特点 $\theta=\varphi=0$
   2. 等效约束力 (叠加时为高副) $F_{S}$ (正对称时为 $0$), $F_{N}$ (反对称时为 $0$)

利用对称性简化结构

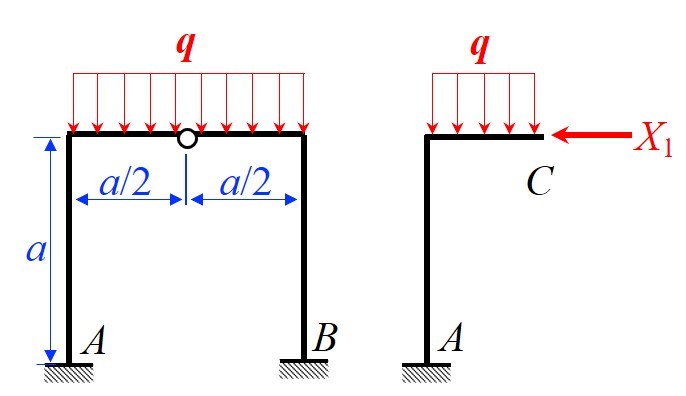
1. 首先判断结构与载荷的对称性
2. 沿结构的对称面截取得到子结构
3. 根据截开点的截面特点, 将其等效为特定约束
4. 判断子结构的自由度并求解超静定问题
5. 根据子结构的受力情况, 形变与对称一侧对称 / 反对称, 得到结构的整体受力与形变
6. 注意对称面截开机构后, 截面的方向与对称面一致, 因此截面上的轴力垂直于对称面, 剪力平行于对称面

额外变形量

额外变形量定义

1. 材料的额外变形体现为材料在约束处已有变形量, 因此几何协调条件等式右侧还有一个从原始到约束的额外变形量 $\Delta'$
2. 额外变形量大小为从原始状态 (经过膨胀 / 未装配) 到约束处的变形量 (通常为位移), 与约束力的方向同向时为正
3. 存在额外变形量时, 立法正则方程为

$$[\delta_{ij}]_{n\times n}[X_j]_n=\{\Delta'_i-\sum_{m=1}\Delta_{iF_m}\}_n$$

热膨胀与装配应力

在静定状态下, 材料长度不匹配时结构能自动调整, 但在超静定状态下, 材料的变形 (装配间隙 / 热膨胀) 受到约束将产生附加内力

弹簧约束

1. 弹簧可将其视为一个滑动铰链支座, 由于弹簧的特殊性, 应优先作为去除约束分析
2. 弹簧也可使用额外变形量法分析, 对于弹簧, 其物体没有变形, 但约束位置 (弹簧自由端) 与弹簧受力有关, 从物体原始位置变形至弹簧自由惯将产生额外变形
3. 注意力的相互作用, 例如当弹簧有向上的约束力时, 弹簧受压, 因此一般额外变形量为负, 有 ($k$ 为弹簧刚度)

$$\Delta'=-\frac{F}{k}$$

冲击载荷

• 在冲击载荷作用下 (具有动能与重力的物体), 弹性体将发生额外变形以将冲击载荷的动能转化为应变能, 此时弹性体将发生远大于平衡状态下的变形
• 定义以下物理量
  1. $P$ 冲击载荷的重力 (受力)
  2. $H$ 冲击载荷到达弹性体前受力的距离
  3. $\delta_d$ 冲击载荷作用下弹性体的变形
  4. $\delta_s$ 无冲击时弹性体的变形
  5. $k$ 弹性体在冲击点的刚度系数
• $\delta_s$ 即弹性体在外力 $P$ 作用下的变形, 可通过卡氏定律求出
• 弹性体某一点的刚度系数满足 $F=kx$, 其中 $F$ 为任意作用在该点上的力, $x$ 为弹性体相应的位移, 可在计算 $\delta_s$ 的同时求出
• 已知刚度系数时, 弹性体的应变能满足 $U=\frac{1}{2}kx^2=\frac{1}{2}F^2/k$ (此式也可用于求弹簧的应变能, 用于卡氏定律)
• 根据冲击载荷的能量完全转化为应变能可得到方程

$$P(H+\delta_d)=\frac{1}{2}k\delta_d^2$$

通过解出方程即可得到 $\delta_d$ (取数值较大的解)

• 根据解出的 $\delta_d$ 与 $k$ 可以计算出动载荷等效的静载荷, 再由等效静载荷计算出等效应力等

$$F_d=k\delta_d$$