压杆稳定问题

1. 压杆稳定问题仅考虑竖直杆件受到理想无偏心压力的情况 (如受压桁架), 受拉时不考虑失稳问题
2. 压杆稳定中, 受压端不能有压力方向的约束力, 否则压力在受压端即被抵消, 不存在压力
3. 需要受到轻微扰动后, 杆件不能回复直线而是继续弯曲并发散, 则称为失稳
4. 设临界压力 $F_{cr}$, 当压力在以下条件下杆件的变形为
   1. $F<F_{cr}$ 杆件受到扰动后快速回复
   2. $F=F_{cr}$ 杆件受到扰动后保持特定的弯曲形状
   3. $F>F_{cr}$ 杆件受到扰动后失稳

细长杆的临界压力

基本公式

1. 在临界压力下弯曲时, 对心压力与弯曲杆件的轴线不再平行, 因此杆件截面上将产生弯矩
2. 此弯矩即使杆件弯曲的内力, 因此杆件保持弯曲状态, 符合临界压力的要求
3. 根据此条件可计算得到, 材料在线弹性状态下临界压力满足公式 $$F_{cr}=\frac{\pi^2EI}{(\mu l)^2}$$
4. 公式中的 $\mu$ 为长度因素, 与杆件所处的约束有关

常见约束下的长度因素

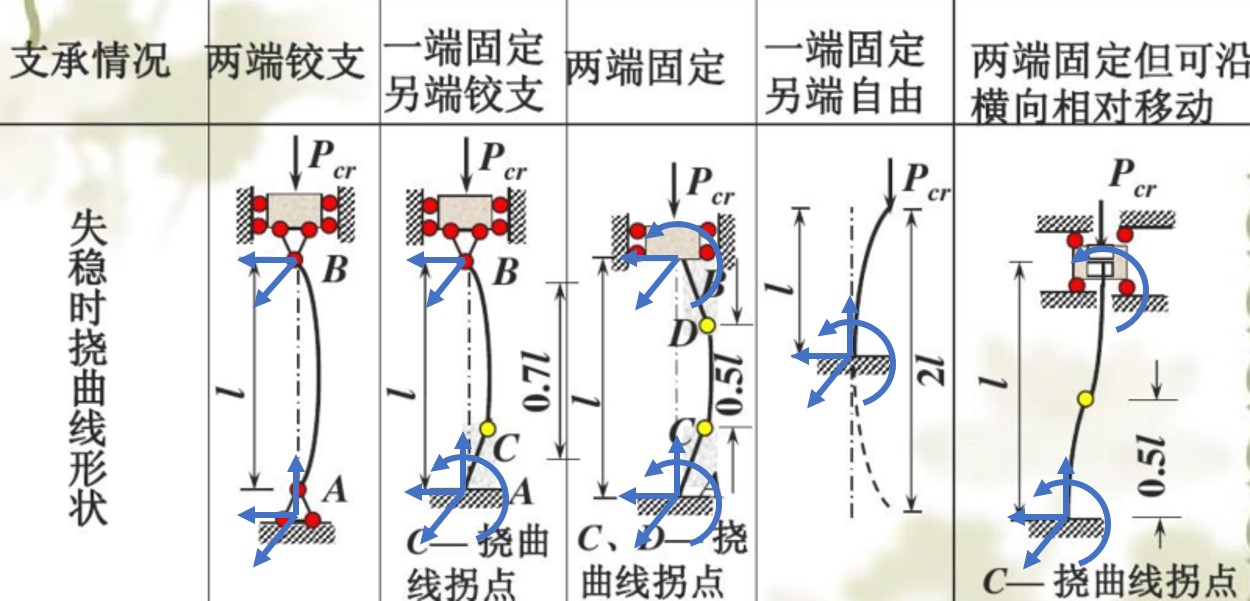
约束	约束方向	长度因素 $\mu$
两端球铰支 (受压端为滑动铰)	$5$	$1$
一端固定, 一端滑动球铰支	$6$	$\approx 0.7$
两端固定 (受压端为轴向滑块)	$7$	$0.5$
一端固定一端自由	$4$	$2$
两端固定 (受压端为横向与轴向滑块)	$5$	$1$
桁架中两端球铰支的二力杆		$1$

欧拉公式使用注意

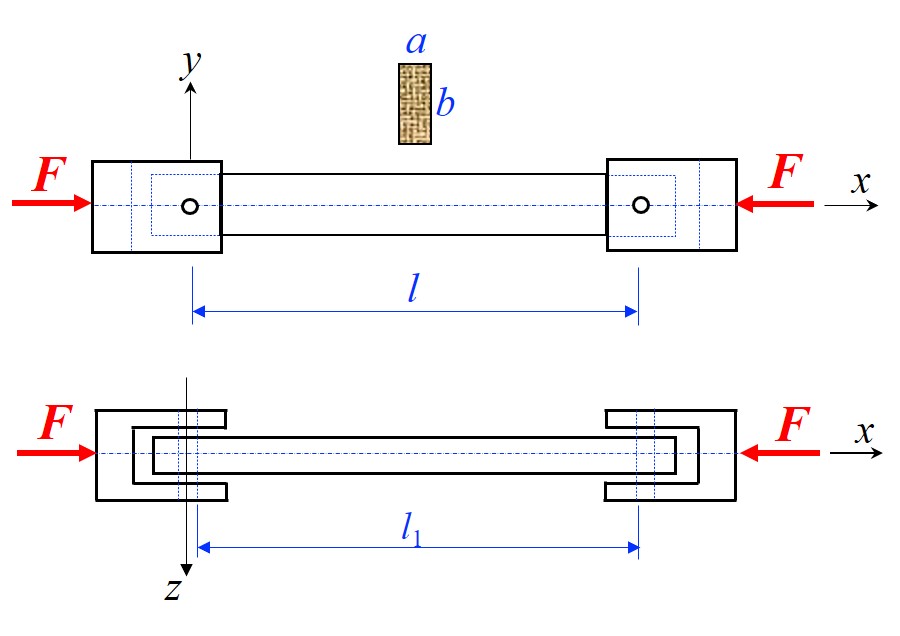
1. 对于无方向性的约束 (如球铰), 公式中 $I$ 为截面上最小的惯性矩
2. 对于有方向性的约束 (如图示平铰约束), 需要从不同弯曲分析, 对于如图约束
   1. 当压感在 $y$ 轴方向发生弯曲时, 属于双球铰约束, 长度从铰圆心开始计, 因此 $\mu=1,\;I=I_z=ab^3/12\,\;L=l$
   2. 当压感在 $z$ 轴方向发生弯曲时, 属于双固定端约束, 长度从未约束处开始计, 因此 $\mu=2,\;I=I_y=ba^3/12,\;L=l_1$

临界压应力

由于认为压应力均匀分布在截面上, 因此可得截面在临界压力下的正应力称为临界压应力 $\sigma_{cr}$ 满足

$$\sigma_{cr}=\frac{F_{cr}}{A}=\frac{\pi^2EI}{A(\mu l)^2}$$

压杆柔度

将临界压应力中与材料无关的量取出, 得到一个仅与杆件状态有关的无量纲系数, 称为柔度 $\lambda$, 满足

$$\begin{split}\sigma_{cr}=\frac{\pi^2E}{\lambda^2}\\ \lambda=\mu l\sqrt{A/I}\end{split}$$

临界柔度

• 由于欧拉临界压力公式中, 要求杆件处于线弹性状态, 因此使用欧拉公式得到的临界应力必须符合条件 $\sigma_{cr}<\sigma_{p}$ ($\sigma_p$ 为材料的比例极限)
• 将 $\sigma_{cr}=\sigma_{p}$ 下的柔度称为线弹性临界柔度 $\lambda_p$, 满足

$$\lambda_p=\sqrt{\frac{\pi^2 E}{\sigma_p}}$$

• 根据 $\lambda_p$ 公式可得其仅与材料性质有关, 与杆件无关, 对于一般钢材料满足 $\lambda_p\approx 100$ (通常由材料的其他属性计算出)
• 同样当杆件处于非线性弹性状态下且未发生屈服时, 也有屈服临界柔度 $\lambda_s$, 满足

$$\lambda_s=\sqrt{\frac{\pi^2 E}{\sigma_s}}$$

(对于脆性材料, 没有屈服则取强度极限 $\sigma_b$)

一般杆件的临界压应力

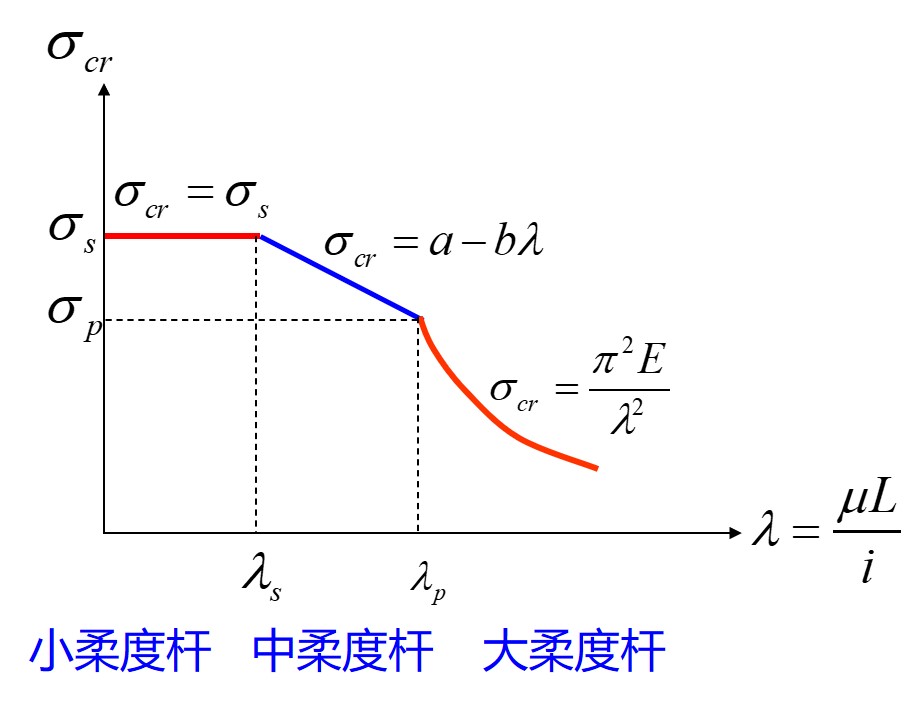
大柔度压杆

1. 满足 $\lambda>\lambda_p$ 的压杆, 也称为细长杆
2. 此时发生弯曲失稳杆件仍处于线弹性状态, 因此可使用欧拉临界压力公式

$$\sigma_{cr}=\frac{\pi^2E}{\lambda^2}$$

中柔度压杆

1. 满足 $\lambda_p>\lambda>\lambda_s$ 的压杆, 也称为中粗杆
2. 此时发生弯曲失稳杆件仍处于非线弹性状态, 欧拉公式不成立, 通过实验插值得到临界压应力

$$\sigma_{cr}=a-b\lambda$$

$a,b$ 为实验得到的系数

短粗杆

1. 满足 $\lambda<\lambda_s$ 的压杆
2. 此时认为受压屈服 / 断裂才是杆件失效的主要形式, 因此直接与 $\sigma_s$ 比较, 不考虑失稳

$$\sigma_{cr}=\begin{cases}\sigma_s,&\text{塑性材料}\\ \sigma_b,&\text{脆性材料}\end{cases}$$

稳定安全系数

与安全系数类似, 定义稳定安全系数 $n_{st}$, 对于临界压力 $F_{cr}$ (对于中柔度杆可通过 $F_{cr}=\sigma_{cr}A$ 计算), 有许用压力

$$F\le[F_{st}]=\frac{F_{cr}}{n_{st}}$$