连接强度计算

薄板受力

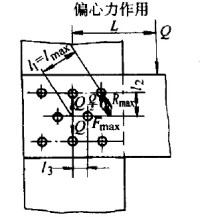
1. 当外力过连接件的形心时, 各个连接件对薄板有受到大小相同且与外力反向平行的支持力, 使之与外力平衡
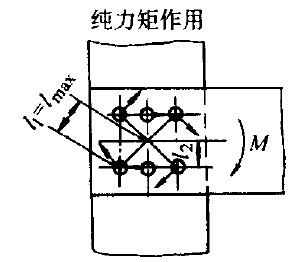
2. 当薄板受矩是, 各个连接件受到, 方向垂直于各自圆心指向连接件形心, 大小与到形心距离成正比的力, 并产生力矩使之平衡
3. 对于复杂 (偏心) 外力, 则将外力平移到连接件形心, 同时各个连接件受到上述两种力的合力 (由于平衡力矩的支持力方向与大小不同, 因此各个连接件受到的合力不同)
4. 对于平行于薄板的力, 分析方法相同, 但螺钉分布在一条直线上

连接件受力

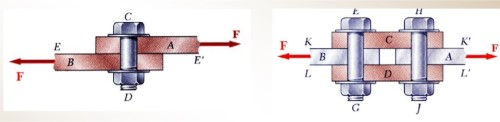
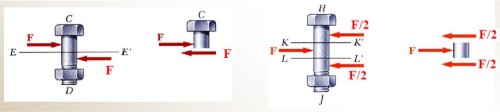
1. 当铆钉对薄板有支持力时, 铆钉自身也将受到等大反向的挤压力
2. 由于铆钉也是静止的, 因此铆钉的合力也为 $0$, 对于不受力的薄板, 为了平衡铆钉自身的受力, 可能也会对不受外力的薄板施加力 (如右图的双剪情况)
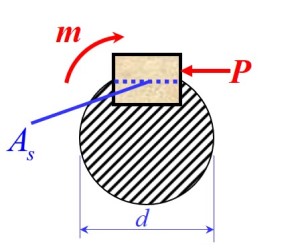
3. 对于键传递扭矩时, 轴的扭矩通过与轴接触的键槽侧面的挤压力传递到键, 在通过与轮毂接触的键槽侧面的挤压力传递到轮毂, 因此键上也存在挤压与受剪 (认为挤压力 $F_{bs}=2M/d$, $d$ 为轴直径)

挤压强度计算

• 当物体的两侧平行平面 (圆柱面) 上受到两个大小不同的, 垂直于平面的外力时 (方向不一定不同), 对物体将会有挤压作用, 使物体变形
• 当连接件对薄板有支持力时, 连接件便受到来自薄板的挤压力 (反作用力), 通过求解薄板 (连接件) 的受力得到连接件的挤压力
• 对于圆柱面, 最大挤压正应力出现在垂直于挤压力直径所在的平面, 且认为挤压正应力均匀分布在此平面上, 因此有最大挤压正应力

$$\sigma_{bs}=\frac{F_b}{A_{bs}}\le[\sigma_{bs}]$$

• 使用许用挤压应力 $[\sigma_{bs}]$ 校核强度 (backside squeeze)
• 其中 $A_{bs}$ 为计算挤压面面积, 即挤压面在挤压力方向的投影, 对于圆柱面即 $A_{bs}=dh$ ($d$ 为直径, $h$ 为挤压高度)

剪切强度计算

• 当物体受到两个大小不同, 方向平行的挤压力时 (可能为 $0$ 或方向相同) , 挤压力作用的交界处将存在剪切作用
• 截取交界面为受剪截面, 将物体分为两个部分, 交界面上将存在剪力与研究部分的挤压力平衡, 剪力平行于被截面及挤压力, 垂直于受力面 (通过力平衡具体计算剪力)
• 认为剪切应力在受剪截面上均匀分布, 因此有剪应力

$$\tau=\frac{F_S}{A}\le[\tau]$$

• 使用许用剪应力 $[\tau]$ 校核强度
• 其中 $A$ 为剪切面的面积, 对于连接件剪切面为圆形, 对于冲孔剪切面为圆弧形

连接板强度计算

1. 分析薄板的强度时, 将铆钉的支持力视为集中外力分布在薄板上, 并以此分析薄板的轴向内力
2. 由于铆钉孔的存在, 将导致薄板的截面面积减小, 也将导致薄板内的应力增大, 成为危险截面