应力状态与强度理论

应力状态理论

应力定义

• 应力通常与内力与截面形状有关, 内力相同截面不同时应力也不同, 但与外力无直接关系
• 对于物体截面上任意点的 $K$ 处的应力为, 以 $Pa(N/m^2)$ 或 $MPa(N/mm^2)$ 为单位

$$\vec{p}=\frac{d\vec{F}}{dA}$$

• 应力为一个矢量 (考虑截面方向则为张量), 定义应力沿截面法向分量为正应力 $\sigma$, 切向分量为切应力 $\tau$
• 定义正应力的正方向为截面指向物体外的法向 (与轴力正方向相同)
• 当正应力 顺时针 旋转 $<90^\circ$ 到达切应力方向时, 认为是切应力的正方向, 并可再投影到两个正交方向上 (切应力方向与截面内力坐标轴无关)
• 在力平衡计算中 (如果需要), 应先使用积分 $F_\sigma=\int \sigma dA\;F_\tau=\int \tau dA$ 将应力合成为合力
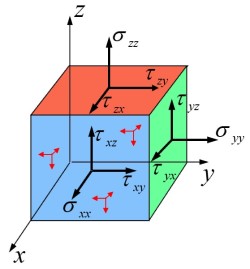
• 对于实际物体, 取其中的一个微立方体, 规定如图所示的三相应力状态
  1. 对于正应力, 下标表示应力所在轴
  2. 对于切应力, 下标 $ab$ 中, $a$ 表示切应力所在微面的方向, $b$ 表示切应力方向
  3. 因此可使用一个 $3\times 3$ 的矩阵 $[\sigma_{ij}]$ 来描述一个微立方体的应力状态

切应力互等原理

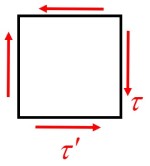
• 对于一个微立方体, 在其相互垂直的平面上, 垂直于平面交线的切应力数值相等
• 且方向均为指向或离开交线
• 由此可得在三相应力状态下, 有 (注意切应力方向)

$$\tau_{ab}=-\tau_{ba}$$

• 根据切应力互等, 应力状态矩阵 $[\sigma_{ij}]$ 为一个实对称矩阵

主应力

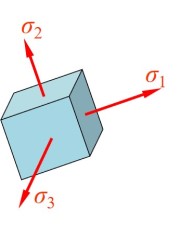
• 由于应力状态矩阵为实对称矩阵, 因此可以对其进行正交变换, 仅旋转坐标轴, 得到一个方向的微面上进存在正应力, 而不存在切应力
• 将坐标变换得到的三个应力称为主应力 $\sigma_1,\sigma_2,\sigma_3$, 主应力与主应力方位客观存在, 并且可以为 $0$
• 按从大到小的顺序确定主应力的次序, 其中 $\sigma_1$ 最大

$$\sigma_1\ge\sigma_2\ge\sigma_3$$

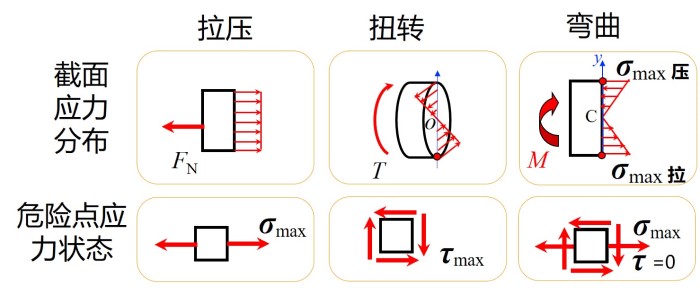
• 如果微立方体的一个面上应力为 $0$ (包括剪应力), 则称为平面应力状态, 注意平面应力状态下仍有三个主应力, 只是其中一个为 $0$
• 对于基本变形, 均为平面应力状态, 具体如下

应力莫尔圆法

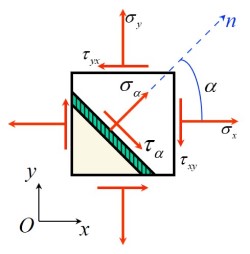
• 对于应力的正方向见应力定义
• 定义截面方位角 $\alpha$ 为 $x$ 轴正方向逆时针旋转到截面法向 $n$ 的角度 (旋转方向相反时取负)
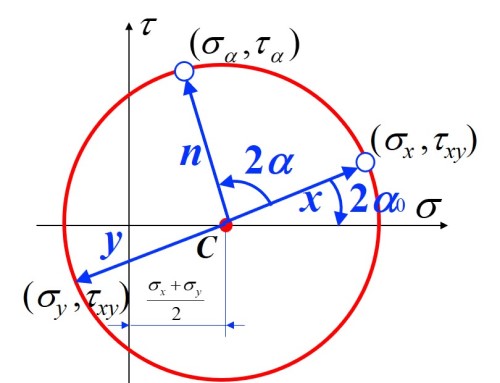
• 通过应力莫尔圆法, 以 $\sigma$ 为 $x$ 坐标, $\tau$ 为 $y$ 坐标建立坐标系, 对于任意截面上的应力状态均可在莫尔圆上体现
• 以莫尔圆上一点所在的半径逆时针旋转 $2\alpha$ 即可得到与该点对应截面夹角为 $\alpha$ 的截面应力状态
• 由此可推出垂直平面的应力状态为莫尔圆的一条直径, 根据切应力互等, 莫尔圆的圆心必定在 $x$ 轴上

莫尔圆求法

当 $x$ 面与 $y$ 面上的应力状态已知时, 通过以下步骤求出莫尔圆

1. 根据切应力互等, $\tau_{xy}=-\tau_{yx}$, 确定 $x$ 面上的切应力即可求出 $y$ 面上的切应力 (注意负号), 并在坐标上标出两个面对应的点, 即可得到莫尔圆的一条直径
2. 根据莫尔圆的性质可得, 莫尔圆的圆心满足

$$\sigma_c=\frac{\sigma_x+\sigma_y}{2}$$

3. 莫尔圆的半径即两点长度的一半

$$R=\frac{1}{2}\sqrt{(\frac{\sigma_x-\sigma_y}{2})^2+\tau_{xy}^2}$$

4. 观察莫尔圆可得, 当 $x,y$ 平面上的 $\tau$ 取最大值时, 即直径垂直于 $x$ 轴, 因此

$$\tau_{max/min}'=\pm R/2$$

5. 当取到主应力方向时, 即直径与 $x$ 轴重合的情况, 在此直径下取得平面内的最大与最小主应力

$$\sigma_{max/min}=\sigma_c\pm R$$

6. 定义 $\alpha_0$ 为主平面的方位角, 通常 $x$ 面的应力状态与最大应力的应力状态半径进存在夹角 $2\alpha_0$ (注意正方向), 因此根据三角关系可得 $\alpha_0$ 满足

$$\alpha_0=-\frac{1}{2}\arctan(\frac{2\tau_{xy}}{\sigma_x-\sigma_y})$$

• 平面应力状态下还有主应力 $0$, 因此三个主应力序号需要具体比较确定
• 对于其他已知条件, 可根据莫尔圆的特点与两个面的夹角求解
• 根据三向莫尔圆可得, 三个方向的主应力可分别组成三个相切的莫尔圆, 因此最大切应力满足 (注意最大切应力不一定在 $xy$ 平面上)

$$\tau_{max}=\frac{\sigma_1-\sigma_3}{2}$$

• 通过莫尔圆求出与方位角为 $\theta$ 时的应力状态

$$\sigma_{\alpha=\theta}=\sigma_c+R\cos[2(\theta-\alpha_0)]$$

注意 $\alpha_0$ 为从 $x$ 方向到主方向的旋转角, $-\alpha_0$ 才是 $x$ 方向应力状态在莫尔圆上的夹角
莫尔圆坐标系中, $\sigma$ 方向对应的是主方向, 不是 $x$ 轴方向

广义胡克定律

泊松比

• 定义横向变形

$$\varepsilon'=\frac{b'-b}{b}$$

其中 $b$ 为原始横向宽度, $b'$ 为变形后的横向宽度

• 在杆件弹性受拉时, 还将发生横向收缩, 其中变形满足比率关系, 称为泊松比 $\mu$ (注意负号, 轴向拉伸时横向收缩)

$$\varepsilon'=-\mu\varepsilon$$

• 根据应变能密度推到可得泊松比与剪切模量之间存在关系

$$G=\frac{E}{2(1+\mu)}$$

• 在多向受拉时, 需要考虑泊松效应对应变的影响

广义胡克定律

• 对于主应力方向上, 微立方体仅受正应力, 仅存在正应变, 因此微立方体的主应力方向即主应变方向, 带入胡克定律可得微立方体的正应变 (还需要考虑泊松比对其他方向应变的影响)

$$\varepsilon_i=\frac{\sigma_i}{E}-\mu(\frac{\sigma_j}{E}+\frac{\sigma_k}{E})$$

• 对于一般方向, 由于同时存在切应力, 因此还将存在切应变

$$\gamma_{ij}=\frac{\tau_{ij}}{G}=\frac{2(1+\mu)}{E\tau_{ij}}$$

• 认为切应变与正应变不耦合, 因此对一般方向的应力状态, 正应变公式依然成立
• 广义胡克定律对平面应力状态同样成立, 仅需取 $\sigma_z=\tau_{ij}=0 (i,j\neq x,y)$

应变莫尔圆法

• 将 $\varepsilon$ 与 $\gamma/2$ 代换 $\sigma$ 与 $\tau$ 即可得到适用于应变的莫尔圆公式
• 对于应变与应力, 其主平面的方位角 $\alpha_0$ 相同
• 由于任意正交方向的应变均可由胡克定律求出对应应力, 因此通常由特殊方向应变求出 $x,y$ 方向应变, 代入胡克定律得到应力, 再使用莫尔圆求解主应力
• 通常切应力较难测量, 因此通常为测出三个不同方向的正应变, 最后合成为平面应力状态, 当测量应变 $\varepsilon_{0^\circ},\varepsilon_{45^\circ},\varepsilon_{90^\circ}$, 根据应变圆可得其与 $x,y$ 方向应力之间满足

$$\begin{cases} \varepsilon_{x}=\varepsilon_{0^\circ}\\ \varepsilon_{y}=\varepsilon_{90^\circ}\\ \gamma_{xy}=\varepsilon_{0^\circ}+\varepsilon_{90^\circ}-2\varepsilon_{45^\circ}\\ \end{cases}$$

• 转换应变与应力时, 需要注意泊松效应的影响, 对于方位角为 $\theta$ 的应力, 其应变为

$$\varepsilon_{\alpha=\theta}=\frac{\sigma_{\alpha=\theta}}{E}-\mu\frac{\sigma_{\alpha=\theta+90^\circ}}{E}$$

对于 $x,y$ 轴上的转化同理
由于泊松效应, 因此当应力 $\sigma=0$ 时, 同方位角下的应变 $\varepsilon$ 不一定为 $0$, 还需要考虑与其夹角为 $90^\circ$ 方向下的应力 ($\sigma_x=0,\sigma_y\neq 0\to\varepsilon\neq 0$)

应变能密度

体积应变

定义微立方体体积的变化率为体积应变 $\theta$

$$\theta=\frac{dV_1-dV}{dV}=\varepsilon_1+\varepsilon_2+\varepsilon_3$$

其中 $dV=dxdydz,\;dV'=(1+\varepsilon_1)(1+\varepsilon_2)(1+\varepsilon_3)dV$

体积改变能密度

将主应力分解为平均值 $\sigma_m=(\sigma_1+\sigma_2+\sigma_3)/3$ 与剩余部分, 平均值部分仅产生体积变化, 对应的应变能称为体积改变能 (注意泊松效应)

$$u_V=\frac{1-2\mu}{6E}(\sigma_1+\sigma_2+\sigma_3)^2$$

畸变能密度

剩余部分仅产生形状变化, 对应的应变能称为畸变能

$$u_d=\frac{1+\mu}{6E}[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2]$$

应变能密度

两部分能量恰好可线性叠加, 构成应变能

$$u=\frac{1}{2}(\sigma_1\varepsilon_1+\sigma_2\varepsilon_2+\sigma_3\varepsilon_3)$$

强度理论

适用 $\sigma_{rx}$ 表示 $x$ 强度理论下的等效应力, 用于与许用应力 $[\sigma]$ 比较

第一强度理论 - 最大拉应力理论

1. 判断依据: 脆性材料断裂的主要原因是最大拉应力达到极限
2. 强度条件:

$$\sigma_{r1}=\sigma_1\le[\sigma]$$

1. 适用条件: 以多向受拉为主的脆性材料, 且 $|\sigma_3|<\sigma_1$

第二强度理论 - 最大正应变理论

• 判断依据: 脆性材料断裂的主要原因是最大伸长应变达到极限
• 强度条件:

$$\sigma_{r2}=\sigma_1-\mu(\sigma_2+\sigma_3)\le[\sigma]\;(\varepsilon_1\le[\varepsilon])$$

• 适用范围 脆性材料单向受拉沿纵向开裂

第三强度理论 - 最大切应力理论

• 判断依据: 塑性材料失效的主要原因是最大切应力达到极限值
• 强度条件:

$$\sigma_{r3}=\sigma_1-\sigma_3\le[\sigma]\;(\tau_{max}\le[\tau])$$

• 适用范围 适用于塑性材料的屈服失效, 但偏于保守

第四强度理论 - 畸变能密度理论

• 判断依据: 塑性材料失效的主要原因是畸变能量密度达到极限值
• 强度条件:

$$\sigma_{r4}=\sqrt{\frac{1}{2}[(\sigma_1-\sigma_2)^2+(\sigma_2-\sigma_3)^2+(\sigma_3-\sigma_1)^2]}\le[\sigma]\;(u_d\le[u_{d}])$$

• 适用范围 与第三强度理论适用条件相同, 当第三强度理论满足时, 自动满足

强度理论在弯扭组合变形的应用

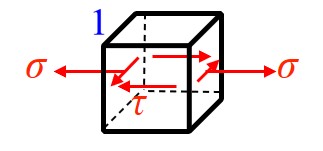
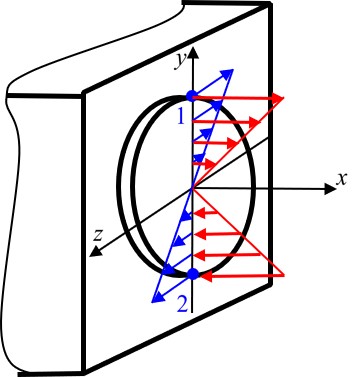
• 对于弯扭组合变形, 其处于拉剪平面应力状态, 在此应力状态下可得 (以下公式也适用于拉扭组合变形等具有相同应力状态的情况)

  1. $$\sigma_{r3}=\sqrt{\sigma^2+4\tau^2}$$

  2. $$\sigma_{r4}=\sqrt{\sigma^2+3\tau^2}$$

• 在弯扭组合变形中, 通常以圆 / 圆筒作为讨论对象, 危险点为截面最外侧上下两点, 此处弯曲正应力与扭转切应力达到最大 (弯曲剪应力为 $0$, 不是忽略)
• 其中危险点的应力满足

$$\sigma=\frac{M}{W_Z}\;\tau=\frac{T}{W_\rho}$$

• 带入弯扭组合变形下的应力后, 根据圆截面上 $2W_Z=W_\rho$ , 可得 (以下结论仅适用于弯扭组合变形)

  1. $$\sigma_{r3}=\frac{\sqrt{M(x)^2+T(x)^2}}{W_Z}$$

  2. $$\sigma_{r4}=\frac{\sqrt{M(x)^2+0.75 T(x)^2}}{W_Z}$$

• 由于圆截面选择任意方向作为弯曲方向均满足弯曲公式, 因此通常将 $y,z$ 轴上的弯矩合成, 有 $M=\sqrt{M^2_z+M^2_y}$
• 对于矩形截面, 其主轴固定为对称轴, 因此不能直接叠加弯矩 $M$, 仅能具体计算出各点的正应力 $\sigma$ (通过叠加得到)