螺纹连接

螺纹连接类型

连接螺纹

三角螺纹

1. 牙型角为 $60^\circ$, 分为粗牙螺纹与细牙螺纹
2. 粗牙螺纹即螺距最大的标准三角螺纹, 用于一般连接, 通过 $MD$ 表示, $D$ 为螺纹的公称直径
3. 细牙螺纹用于要求强度大或薄壁零件与微调装置, 也可用于密封, 通过 $MD\times p$ 表示, $p$ 为螺距

管螺纹

牙型角为 $55^\circ$, 用于有紧密性要求的管件连接, 本质为英制细牙螺纹

传动螺纹

1. 梯形螺纹 应用最广泛的传动螺纹
2. 锯齿形螺纹 用于单向传动
3. 矩形螺纹 传动效率最高, 但齿根强度低

螺纹主要参数

符号	含义	说明
$d/D$	大径 (公称直径)	在螺杆中使用 $d$, 表示外螺纹的牙顶, 在螺孔中使用 $D$, 表示内螺纹的牙底
$d_1/D_1$	小径	在螺杆中使用 $d_1$, 表示外螺纹的牙底, 在螺孔中使用 $D_1$, 表示内螺纹的牙顶
$d_2/D_2$	中径	在螺杆中使用 $d_2$, 在螺孔中使用 $D_2$, 螺纹在此圆柱面上牙厚与牙间相等
$p$	螺距	相邻两牙对应点的轴向距离 (不一定在同一条螺旋线上)
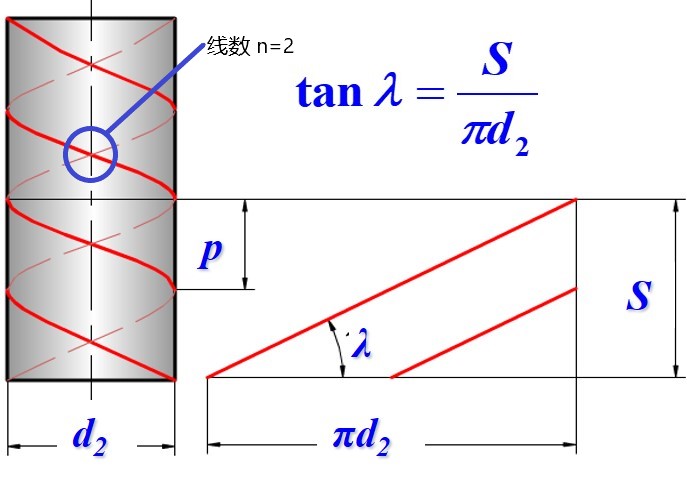
$n$	线数	即螺旋线数, 对于连接螺纹通常 $n=1$
$S$	导程	同一条螺旋线上相邻两牙对应点的轴向距离, 同时也是螺母旋转一周, 相对轴线的移动距离, 满足 $S=np$
$\lambda$	升角 (导程角)	中径圆柱展开面上, 螺旋线与端面的夹角
$\alpha$	牙型角	螺纹牙型两侧边的夹角
	螺纹旋向	对于右旋螺纹, 右手顺时针旋转可将螺母从上到下拧紧

螺纹副的受力分析

分析模型

1. 将螺柱固定, 并采用矩形螺纹, 螺母承受载荷并在螺柱上滑动
2. 将螺柱展开, 简化螺母为滑块, 即可得到受力模型
3. 模型中
   1. 螺母受到来自螺柱的支持力 $N$, 与竖直方向夹角为 $\lambda$
   2. 螺母还受到来自螺柱的滑动摩擦力 $f_v=\mu_v N$ , 与 $N$ 合成后有合力 $R$. 由于 $f_v$ 垂直于 $N$, 因此 $N,f_v,R$ 构成直角三角形, $N$ 与 $R$ 间有夹角 $\rho_v$ (当量摩擦角)
   3. $R$ 的竖直分量与载荷 $F_a$ 平衡
   4. $R$ 的水平分量与螺旋副阻力矩 $T_1=F_t\frac{d_2}{2}$ 产生的圆周力 $F_t$ 平衡

克服载荷移动时

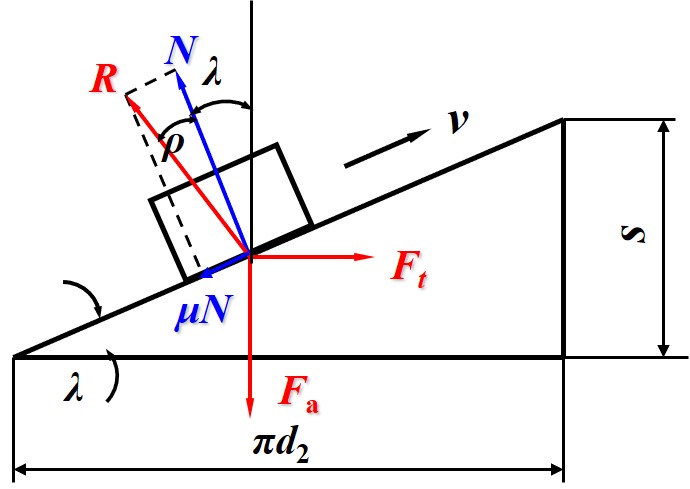
• 螺母在克服载荷匀速上升时, 螺母移动方向 $v$ 与外载荷 $F_a$ 方向相反, 与圆周力 $F_t$ 方向相同, 因此 $F_a$ 为阻力, $F_t$ 为动力
• 此时 $\rho$ 与 $\lambda$ 同向, 因此圆周力满足

$$F_t=F_a\tan(\lambda+\rho_v)$$

• 此时的机械效率满足

$$\eta=\frac{F_aS}{2\pi T}=\frac{\tan\lambda}{\tan(\lambda+\rho_v)}$$

通过增大导程角 $\lambda$ 可提高螺旋副的效率

• 当螺纹存在预紧力时, 也将有载荷 $F_a$, 此时的外力矩为螺旋副阻力矩 $T_1$ , 传递到螺柱上使螺柱受扭

在载荷作用下滑动时

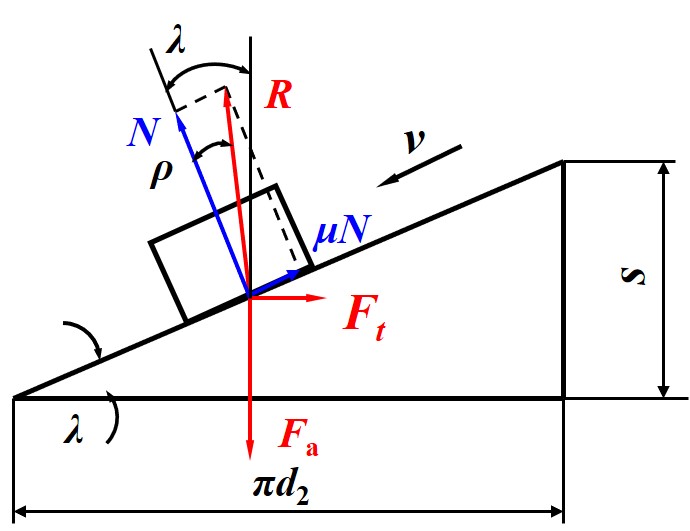
• 螺母在载荷作用下匀速下滑时, 螺母移动方向 $v$ 与外载荷 $F_a$ 方向相同, 因此 $F_a$ 为动力
• 此时 $\rho$ 与 $\lambda$ 反向, 因此圆周力满足

$$F_t=F_a\tan(\lambda-\rho_v)$$

• 注意到当 $\lambda\le\rho_v$ 时, 即使没有外圆周力 $F_t$, 存在静摩擦力 $f=0\sim\mu N$ 可以与载荷 $F_a$ 平衡, 此时螺纹具有自锁性

当量摩擦角

• 当量摩擦角即滑动摩擦 $f$ 与 $N$ 的夹角, 由于 $\mu$ 恒定, 因此此角度恒定满足

$$\rho_v=\arctan\mu_v$$

• 对于三角螺纹, 由于摩擦力来自实际支持力 $N'$ , 而竖直方向的支持力 $N$ 为 $N'$ 的分量, 因此将产生更大的摩擦系数 $\mu_v=\mu/\cos\beta$, 有利于自锁 ($\beta$ 为牙侧角)

螺纹连接设计

螺纹连接基本类型

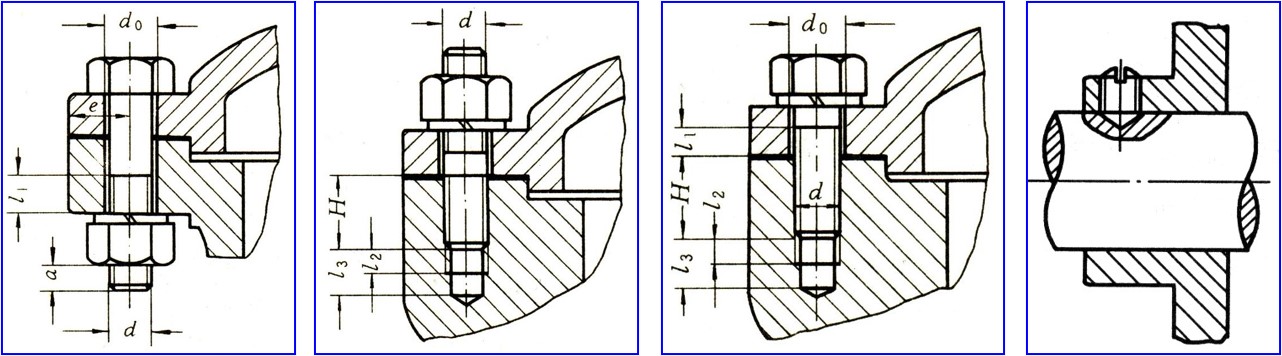
普通螺栓连接

1. 用于被连接件不厚的场合, 最常见
2. 两个被连接件中的两通孔均为光孔, 且不与螺栓接触
3. 注意与铰制孔用螺栓连接区分, 由于以受拉为主, 因此也称为受拉螺栓

双头螺柱连接

1. 被连接件之一太厚且常拆 (拆卸时仅需将螺母拆下即可分离两连接件)
2. 通孔为光孔, 且不与螺柱接触
3. 盲孔上有螺纹

螺钉连接

1. 被连接件之一太厚且不常拆 (需要拆出整段螺钉, 容易使螺钉损坏)
2. 通孔为光孔, 且不与螺柱接触
3. 盲孔上有螺纹

紧定螺钉连接

常用于固定轴上零件

铰制孔用螺栓连接

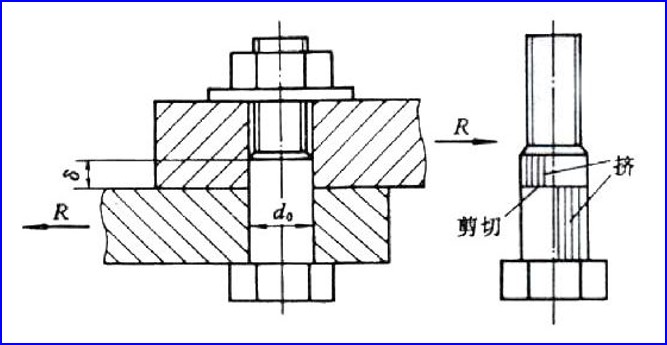
1. 使用场合与普通螺栓类似, 当能承受更大的横向载荷且定位精度高
2. 两个被连接件中的两通孔均为光孔, 且与螺栓有过渡配合
3. 几乎不承受拉力, 以受剪为主因此称为受剪螺栓

螺纹连接防松

预紧力

1. 通过预紧螺纹连接, 防止连接松脱, 并使接合面面紧密接触产生摩擦力承受横向工作载荷 (见强度分析)
2. 通过控制上紧时的力矩以控制预紧力, 满足 $T\approx 0.2F'd$

摩擦放松

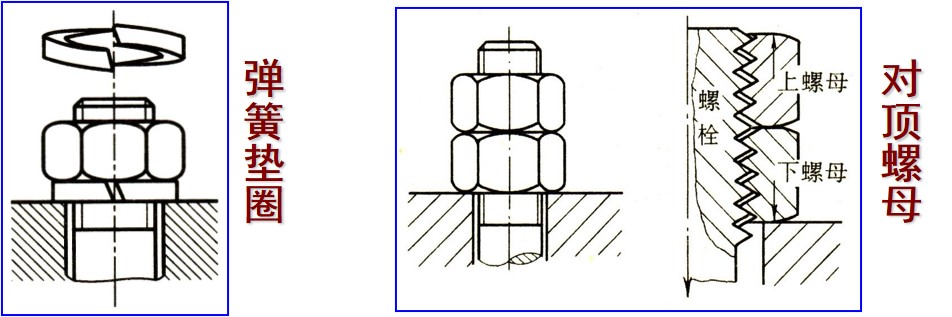
1. 弹簧垫圈 最常用的放松方式, 注意弹簧垫圈的旋向必须与螺旋副的旋向相反, 因此弹簧垫圈一般为左旋 (根据开口判断)
2. 对顶螺母防松

机械防松

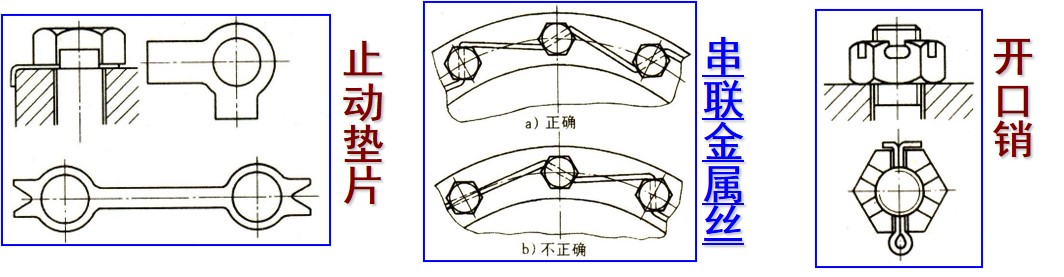
1. 止动垫片
2. 串联金属丝 注意方向不可错, 当中间螺母松动时 (逆时针旋转), 两侧螺母上紧 (顺时针旋转) 才是正确的连接方向
3. 开口销

其他设计要求

1. 合理布置螺栓, 尽量将螺栓远离接合面的对称轴布置, 使其受载减小
2. 合理确定螺栓的间距和边距, 保证足够的扳手空间
3. 同一螺栓组, 螺栓材料与尺寸应相同, 以便减少零件规格
4. 支承面应光洁, 平整, 并与轴线垂直

螺纹连接强度分析

普通螺栓的实际受载分析

普通螺栓连接仅承受轴向载荷

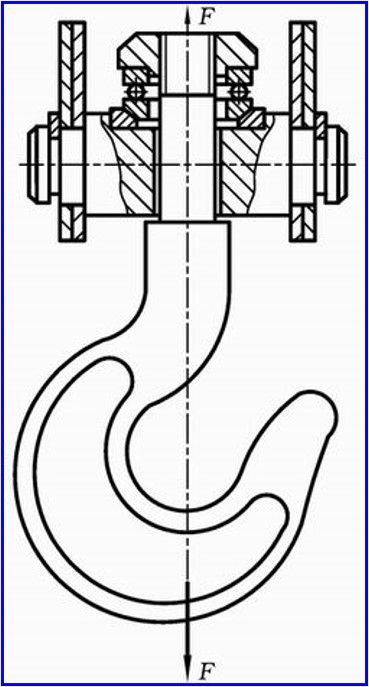
1. 在吊钩等结构中螺纹连接承受轴向载荷, 不需要预紧力
2. 当螺栓连接仅承受轴向工作载荷时, 依靠螺纹自锁即可保证连接
3. 此时螺柱仅受到轴向拉力, 大小即为螺栓所受的轴向载荷 $F$

普通螺栓连接仅承受横向载荷

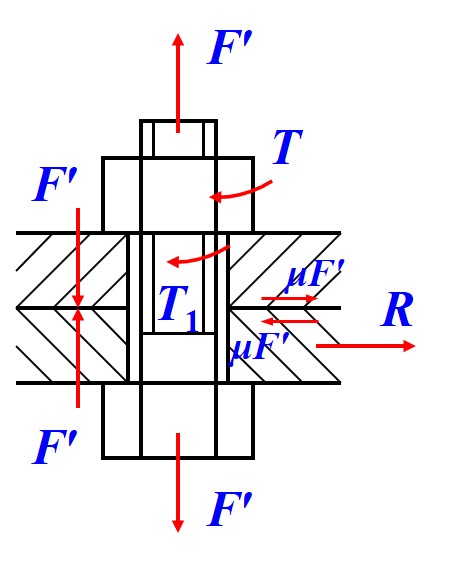
1. 由于普通螺栓与连接件不接触, 因此普通螺栓不能直接承受横向载荷
2. 通过螺母上的预紧力, 使各被连接件压紧, 并使被连接件产生摩擦力用于承受横向载荷
3. 根据摩擦力性质可得, 预紧力越大, 能承受的横向载荷越大, 因此需要根据横向载荷的大小选择预紧力, 满足 $F'=\frac{K_f F_{rm}}{\mu m}$
   1. $F'$ 螺栓上的预紧力
   2. $\mu$ 接合面的摩擦系数
   3. $m$ 接合面对数
      • 当受载荷被连接件的两个面均与其他件接触时, 每个面的摩擦力可分摊一半的载荷, 因此 $m=2$
      • 当仅有两个被连接件时, 仅有一个面提供摩擦力, 因此 $m=1$
   4. $K_f$ 摩擦力可靠性系数, 取 $K_f=1.1\sim 1.3$
   5. $F_R$ 连接件所受的横向载荷, 注意横向载荷加载在被连接件上, 单个螺栓具体承受的横向载荷需要通过受力分析得到 (通常为均匀分布)
   6. $F_{rm}$ 螺栓所承受的最大横向载荷 (用于选型, 需要具体计算), 当螺栓均匀承受载荷时, 则有 $F_{rm}=F_R/z$

普通螺栓连接承受轴向与横向载荷 (仅受轴向载荷但有预紧力)

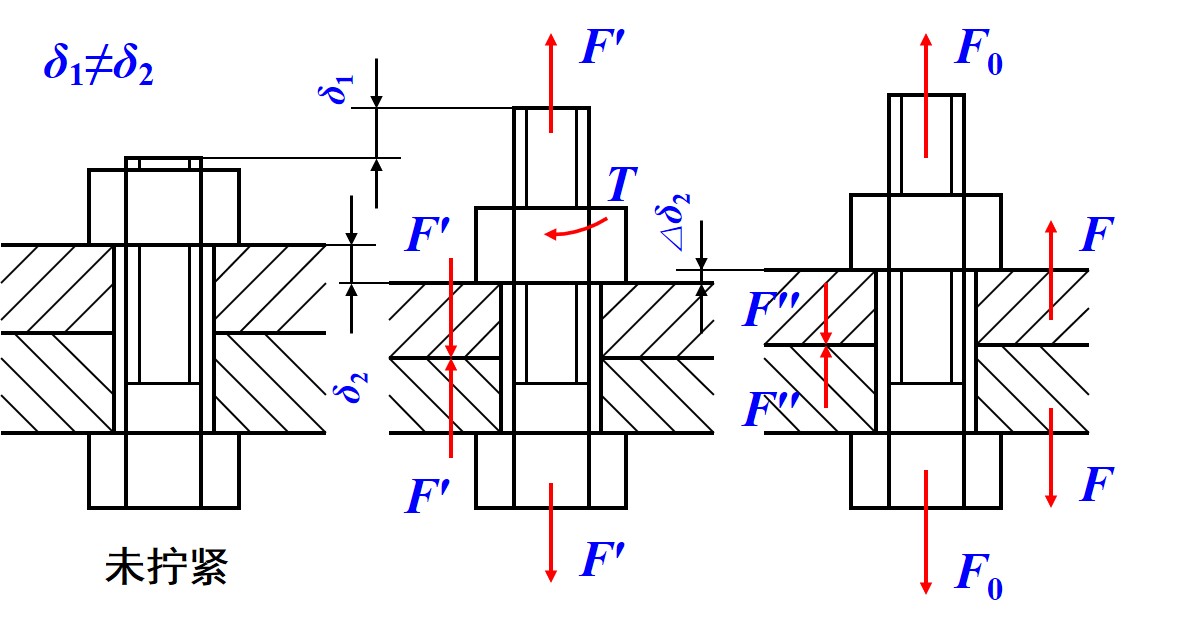
• 当螺栓受预紧力的同时又承受与预紧力反方向的轴向载荷时, 螺栓处于超静定受力状态, 且实际预紧力与承受的实际拉力均改变
• 螺栓实际的预紧力, 称为剩余预紧力 $F''$, 螺栓受到的实际拉力称为总拉力 $F_0$, 轴向载荷 $F$ 不变
• 根据螺栓的受力平衡可得到物理方程 (可用于计算剩余预紧力)

$$F_0=F''+F$$

• 带入几何协调条件可得到总拉力满足 (注意式中使用预紧力 $F'$)

$$F_0=F'+\frac{C_1}{C_1+C_2}F$$

其中 $C_1$ 为螺栓的刚度 (受轴向载荷拉伸变形), $C_2$ 为被连接将的刚度 (受螺母挤压变形), 包括垫片等, $\frac{1}{C_2+C_1}$ 体现几何协调

• 除计算 $F_0$, 还需要校核 $F''>0$, 否则被连接件之间将有缝隙, 无法承受载荷; 对于气密性要求高的情况, 应保证 $F''=1.5\sim 1.8 F$
• 对于轴向载荷大的情况, 应采用金属垫片等增大 $C_2$, 减小轴向载荷

普通螺纹连接的强度计算

主要失效形式

1. 普通螺栓 (受拉螺栓) 的主要失效形式为螺栓杆的塑性变形或断裂
2. 其中危险截面为螺栓小径所对应的剖面

预紧力下的螺旋副阻力矩

• 螺栓在预紧力作用下受拉, 使螺栓中产生拉应力 $\sigma=F'/A$
• 由受力分析可得, 螺栓在承受预紧力时, 还要承受螺旋副阻力矩 $T_1$, 因此螺柱还会受扭, 产生扭转切应力, 对于一般三角螺纹连接满足 $\tau=T_1/W_\rho\approx 0.5\sigma$
• 通过第四强度理论得到计算强度, 有

$$\sigma_{ca}=\sqrt{\sigma^2+3\tau^2}\approx 1.3\sigma=\frac{1.3F'}{A}$$

• 因此对于受横向载荷的情况下有 $F_v=1.3F'\;F_v=1.3F_0$

等效拉力

通过当量拉力 $F_v$ 等效表示螺栓的不同受力状况

• 仅受轴向载荷

$$F_v=F$$

• 仅受横向载荷

$$F_v=1.3F'=1.3\frac{K_f F_{rm}}{\mu m}$$

• 同时承受轴向与横向载荷 (或仅受轴向载荷但有预紧力)

$$F_v=1.3F_0=1.3(F'+\frac{C_1}{C_1+C_2}F)$$

强度校核

使用普通螺栓在危险截面 (小径剖面) 上的拉应力校核强度有

$$\sigma_{ca}=\frac{F_v}{\frac{1}{4}\pi d_1}\le[\sigma]$$

螺栓选择

通过螺栓的当量拉力选择螺栓的小径, 并以此选择螺栓的型号

$$d_1\ge\sqrt{\frac{4F_v}{\pi [\sigma]}}$$

铰制孔用螺栓连接受力与强度分析

受力分析

1. 铰制孔用螺栓通过与通孔之间的挤压直接承受横向载荷, 因此预紧力较小, 可忽略
2. 螺栓受到剪切与挤压作用, 可通过投影法得到螺栓的剪切应力与挤压应力

主要失效形式

由于螺杆受剪切, 因此主要失效形式为螺栓杆被压溃或剪断

螺栓材料的性能等级

1. 通过两个数字组合 $a.b$ 表示螺栓材料的性能等级
2. 螺栓的抗拉极限满足 $\sigma_b=a\times 100 (MPa)$
3. 螺栓的屈服强度满足 $\sigma_s=\frac{b}{10}\times\sigma_b=a\cdot b\cdot 10 (MPa)$

---

连接强度计算

见材料力学的有关介绍