蜗轮蜗杆传动

仅讨论普通圆柱阿基米德蜗杆传动

传动特点

基本参数

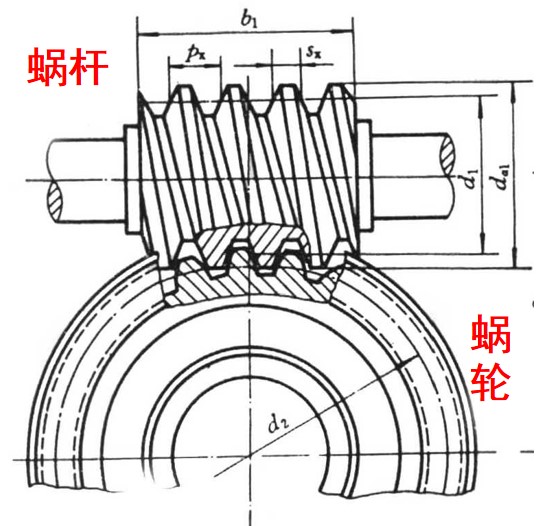
• 定义蜗轮蜗杆传动的几何尺寸以中间平面上的尺寸为主, 中间平面即过蜗杆轴线, 垂直于涡轮轴线的平面
• 在中间平面下, 蜗轮蜗杆相当于齿轮齿条啮合
• 通常蜗杆为主动件, 蜗轮为从动件, 因此蜗杆的参数采用下标 $1$

蜗杆的基本参数

为了简化蜗杆制造, 蜗杆的外形已完全标准化, 并通过铣削加工蜗杆, 滚刀加工蜗轮, 因此, 以下参数均为标准值

名称	符号	含义
蜗杆头数	$z_1$	即蜗杆上螺旋线的数目
蜗杆分度圆直径	$d_1$	蜗杆分度圆上采用标准值, 其中蜗杆分度圆直径也属于标准值
模数	$m$	由蜗杆特性可得, 蜗杆轴向与蜗轮端面上模数相同
压力角	$a$	对于普通圆柱阿基米德蜗杆传动, 采用标准值 $a=20^\circ$, 并且蜗杆轴向与蜗轮端面上压力角相同
直径系数	$q$	由于蜗杆的模数与分度圆直径均为标准值, 因此定义其比值为直径系数 $q=d_1/m$, 注意与齿轮不同, 得到的结果不是齿数

蜗杆几何尺寸

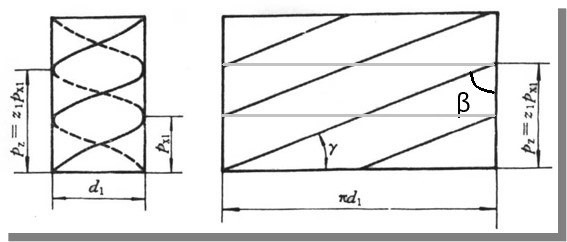
分度圆柱面上的尺寸

• 螺旋线在分度圆柱面上的投影如图左侧图形
• 同一螺旋线在蜗杆轴线方向的距离为导程 $p_z=z_1 p_x$
• 相邻螺旋线在蜗杆轴线方向的距离为螺距 $p_x$
• 由于中间面上, 蜗杆的投影为齿条, 齿条齿距即相邻螺旋线在蜗杆轴线方向的距离, 因此螺距满足 (蜗杆在轴向与端面上模数相同)

$$p_x=\pi m$$

圆柱面展开尺寸

• 在蜗杆的分度圆柱面上展开可得到如图矩形
• 螺旋线在展开矩形上呈平行斜线, 其中同一条螺旋线的投影在矩形的左右交点连线平行于端面
• 定义螺旋线与端面的夹角为导程角 $\gamma$, 由图可得, 导程角满足

$$\tan\gamma=\frac{p_z}{\pi d_1}=\frac{z_1\pi m}{\pi d_1}=\frac{z_1}{q}$$

• 定义端面与法面的夹角为螺旋角, 螺旋角与导程角满足关系 $\beta=90^\circ-\gamma$

蜗轮蜗杆传动参数

啮合条件

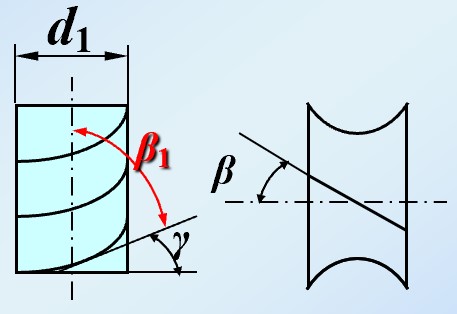
当蜗轮蜗杆的轴线交错角为 $90^\circ$ 时, 蜗轮蜗杆正确啮合需要满足蜗轮的螺旋角与蜗杆的导程角大小相同, 且旋向相同, 即 $\beta_2=\gamma_1=90^\circ-\beta_1$

传动比

• 对于蜗杆的分度圆柱展开, 螺旋线与矩形一侧的交点相当于蜗杆中中间面上齿条的齿形
• 蜗杆转动一圈, 相当于矩形边从一侧移动到另一侧 (方向由转向决定), 矩形边与展开螺旋线的交点反映了齿条齿形的移动
• 因此可得, 蜗杆转动一圈, 等价于中间面上的等价齿条移动一个导程 $p_z$
• 蜗轮在中间面的投影为齿轮, 因此蜗杆转动一圈, 等价齿轮转动 $p_z$
• 可得蜗轮蜗杆传动满足关系 (注意与齿轮不同, 蜗杆传动的出动比不能使用分度圆的比值)

$$i=\frac{n_1}{n_2}=\frac{\pi mz_2}{p_z}/1=\frac{z_2}{z_1}$$

变位系数

• 通常仅对蜗轮进行变位, 即仅有变位系数 $\chi_2$
• 与齿轮齿条相同, 变位后中心距满足

$$m\chi_2+a=a'$$

其中 $a'$ 为变位后的中心距

• 由齿轮齿条变位得, 变位时分度圆上齿宽与齿距变化, 但仍为节圆 (齿条齿形压力角处处相等, 为标准压力角, 因此节点依然为分度圆)
• 蜗轮蜗杆变位通常用于凑中心距与微调传动比

设计分析

相对滑动

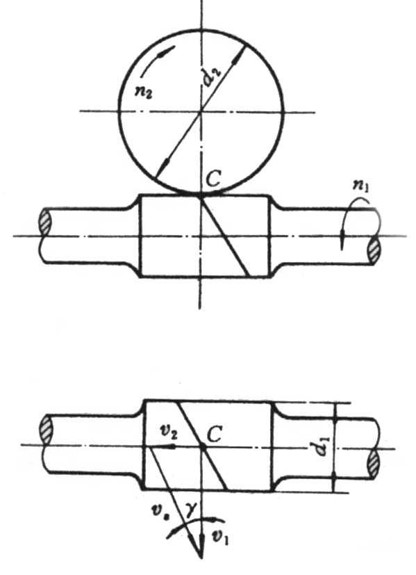
• 对于齿轮传动, 两齿轮为纯滚动, 接触点上不存在滑动, 因此传动效率高
• 对于蜗轮蜗杆传动, 令蜗轮静止, 蜗杆相对于蜗轮运动, 在接触点处存在相对滑动
• 相对滑动速度的两个分速度分别来自蜗杆转动 $v_1$ 与蜗轮转动 $v_2$
• 由于

$$\frac{v_1}{v_2}=i\frac{d_1}{d_2}=\frac{z_2}{z_1}\frac{z_1p_x/\tan\gamma}{z_2 p_x}=\frac{1}{\tan\gamma}$$

可得两个速度之间的夹角为 $\gamma$

• 因此滑动速度大小满足

$$v_s=\frac{v_1}{\cos\gamma}$$

受力分析

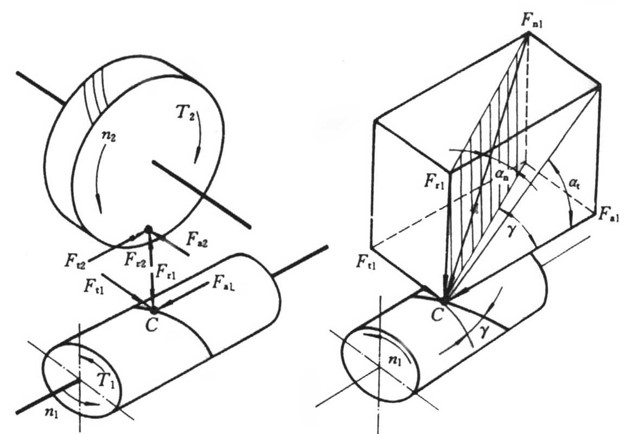
• 通常蜗杆为主动轮, 因此蜗杆以 $1$ 为下标
• 接触点上的力垂直齿面指向蜗轮 / 蜗杆内部
• 由于齿形为螺旋形, 因此接触力共可分解为三个方向的力
• 注意由于蜗轮蜗杆轴线垂直, 因此两零件的径向与圆周方向不同

蜗杆受力

1. 蜗杆作为主动轮, 受到一个阻碍其转动的圆周力 $F_{t1}$, 与其转动方向相反, 并在接触点上与分度圆柱面像切
2. 由于齿面倾斜 (相对于水平面) , 接触点上的径向力 $F_{r1}$ 垂直齿面向里
3. 由于螺旋状的齿形, 因此蜗杆还收到一个轴向力 $F_{a1}$, 可通过右旋右手定则, 根据蜗杆转向确定

蜗轮受力

1. 蜗轮作为从动轮, 圆周力 $F_{t2}$ 为动力, 与蜗轮转向相同, 与蜗杆的轴向力 $F_{a1}$ 平衡
2. 同样蜗轮也有径向力 $F_{r2}$ 并于蜗杆的径向力平衡
3. 蜗轮的轴向力 $F_{a2}$ 与蜗轮的圆周力 $F_{t1}$ 平衡

转矩关系

• 通过传递的功率表示转矩有

$$T=P/n$$

• 因此蜗杆与蜗轮转矩满足关系 (注意由于蜗轮传动效率低, 需要考虑机械效率 $\eta$)

$$\frac{T_2}{T_1}=\frac{P_2/n_2}{P_1/n_1}=\eta i$$

• 因此蜗轮的转矩满足 (蜗杆转矩通过传递效率计算)

$$T_2=\eta iT_1$$

机械效率

• 蜗杆传动总效率包括
  1. 啮合损耗功率 $\eta_1$
  2. 轴承摩擦损耗功率 $\eta_2$
  3. 搅油损耗功率 $\eta_3$
  4. 总效率满足 $\eta=\eta_1\eta_2\eta_3\approx\eta_1$
• 定义当量摩擦角 $\rho_v$, 与摩擦系数满足关系 $\tan\rho_v=f_v$
• 当蜗杆主动时, 近似满足

$$\eta_1=\frac{\tan\gamma}{\tan(\gamma+\rho_v)}$$

• $\eta$ 随 $\gamma$ 增大而增大, 而 $\gamma$ 随头数增加而增加
• 因此增加头数可以增大传动效率, 但一般 $\gamma<28^\circ$, 继续增大将导致加工难度增大, 且效率提升低
• 认为 $\gamma<\rho_v$ 或 $\eta<50\%$ 时, 蜗轮蜗杆具有自锁性, 此时一般有 $z_1=1$

失效形式

蜗杆采用耐磨强度高的 45钢或合金钢, 蜗轮则采用磨擦系数低的铜合金 (高速使用铸锡青铜, 低速使用铸铝青铜), 由于铜合金强度低, 因此一般失效发生在蜗轮上

齿面点蚀与胶合

1. 当蜗轮材料为铸锡青铜时, 主要失效形式为齿面点蚀
2. 当蜗轮材料为铸铝青铜时, 主要失效形式为齿面胶合
3. 对于两种失效形式, 均需要校核齿面的接触疲劳强度
4. 由于高温下容易导致齿面胶合, 且蜗轮蜗杆传动摩擦发热大, 因此还需要热平衡计算

齿面折断

仅当 $z_2>80$ 或强烈冲击载荷时可能发生, 需要校核弯曲强度, 一般不校核

接触疲劳强度计算

1. 由于中间平面上蜗杆传动类似于斜齿条斜齿轮传动, 使用赫兹公式计算接触强度, 公式按斜齿轮推导
2. 设计时, 通过疲劳强度计算得到 $m^2d_1$, 并通过此参数选择蜗杆参数 ($m$ 与 $d$ 均为标准值)

润滑与散热设计

润滑

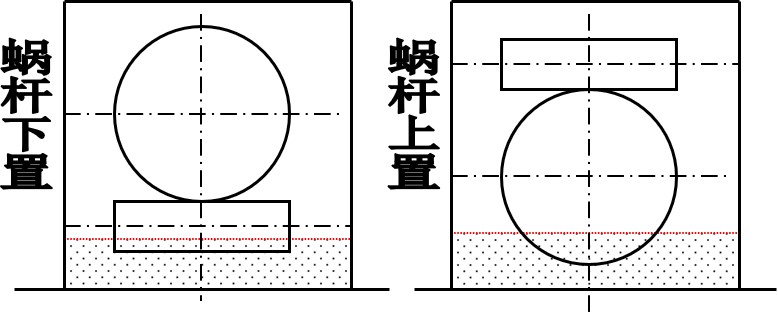
1. 当 $v_1<4$, 采用蜗杆下置, 搅油损耗大, 但润滑效果好
2. 当 $v_1>4$, 采用蜗杆下置, 避免搅油损耗

散热

由热平衡条件可得, 增大散热面积与改善散热条件可以降低热平衡时的工作油温, 因此可采用以下方法降低油温

1. 在箱体外壁增加散热片
2. 在蜗杆轴端增加风扇
3. 在油池中使设置冷却管