V 带传动与链传动
大约 13 分钟
V 带传动设计
设计分析
几何分析
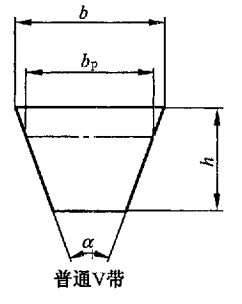
对于 V 带轮的几何尺寸的选用标准值, 可参考 GB/T 11544
基准面
- 定义 V 带轮弯曲时的中性面位置为基准面
- 基准面在带轮上构成圆周即节圆
| 参数名 | 字母代号 | 定义 |
|---|---|---|
| 节宽 | 基准面在带轮截面上的宽度 | |
| 基准长度 | 整根 V 带沿基准面的长度 | |
| 楔角 | 标准值 , V 带截面底部延长线的夹角 |
侧面尺寸
对于简图, 通常绘制带轮在节圆上的形态, 截面参数也是相对于节圆而言
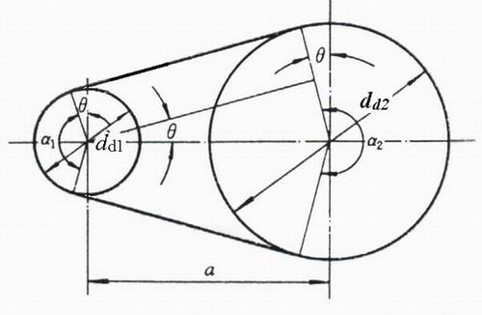
| 参数名 | 字母代号 | 定义 |
|---|---|---|
| 带轮包角 | V 带与带轮接触圆弧的圆心角, 通常 | |
| 中心距 | 两个带轮轴之间的距离 | |
| 基准直径 | 带轮上基准面到轴心的距离即节圆直径 |
力学分析
受力分析
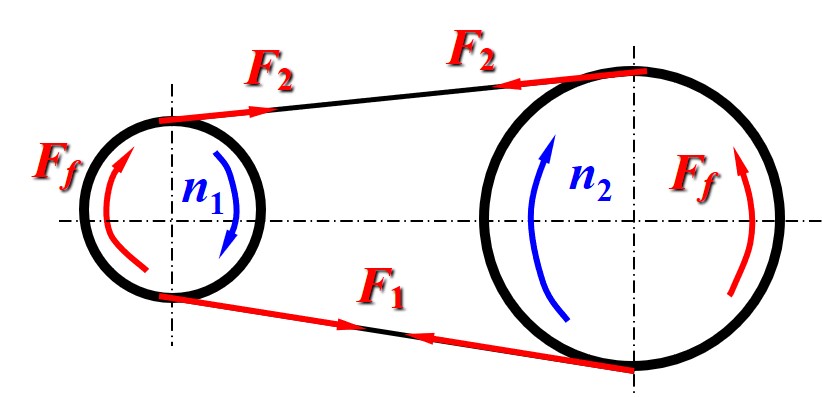
- 当转动时, 带轮将受到来自 V 带的摩擦力
- 在静止情况下, 主动轮以 转动, 从动轮静止, 摩擦力总是使物体相对静止
- 初始状态下, 主动轮转动, V 带静止, V 带相对于主动轮向与转动反方向移动, 因此受到转动方向的摩擦力, 因此 V 带在主动轮一侧, 来自主动轮的摩擦力 与主动轮转动方向相同
- 初始状态下, V 带转动, 从动轮静止, V 带相对于从动轮向与转动同方向移动, 因此受到与转动方向相反的摩擦力, 因此 V 带在从动轮一侧, 来自从动轮的摩擦力 与从动轮转动方向相反
- 沿中线截开 V 带可得, 为了平衡摩擦力, V 带内还存在正拉力 与 , 并且 (截面法)
- 得到 V 带的受力如图, 其中 与 为内力
受力计算
- 对 V 带采用截面法, 分析其中一侧的拉力 与 与摩擦力的关系
- 定义有效拉力
- 带轮在安装时, 内部就已经存在拉力, 称为预紧力
- 当带轮匀速转动时 (不考虑角加速度与转动惯量的问题), 分析带轮上受力如图, 对于单个带轮, 根据力矩平衡有
- 假设带长不变, 作用在 V 带上的总拉力不变, 因此有
- 定义非圆弧上的 V 带中, 由于 , 两侧拉力为 的一边为紧边, 另一边为松边
- 根据欧拉公式, 当达到静摩擦极限 时 ( 摩擦系数, 包角)
- 整理公式可得
应力分析
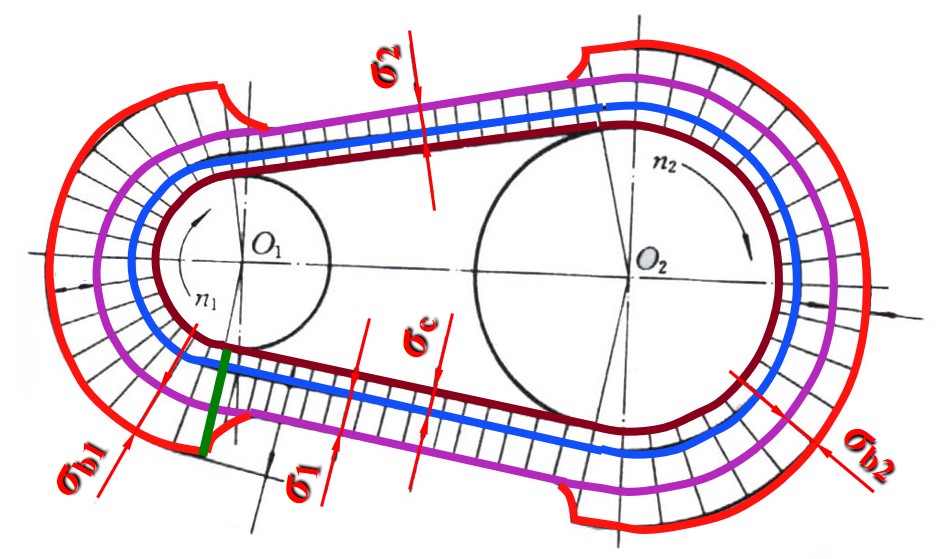
- 拉应力
- 由 V 带受力可得, V 带处处存在正拉力, 其中紧边与松边的正拉力即 与 , 圆弧段上则介于中间
- 紧边拉应力为
- 松边拉应力为
- 接触圆弧拉应力
- 因此紧边拉应力最大, 松边最小, 圆弧介于中间
- 离心拉应力
- 带轮转动时, 圆弧上的 V 带还受到一个离心力
- 通过两侧的额外拉力, 与离心力平衡, 此额外拉力产生的应力称为离心拉应力 ( 为单位长度的 V 带质量)
- 由于此额外拉力在圆弧上处处相同, 为了平衡, 此拉力在两边上也必定相同, 因此离心拉应力对于整个 V 带上各点相等
- 弯曲应力
- 由于 V 带在带轮部分弯曲, 因此与带轮接触的部分还有弯曲拉应力, 而在两边上不存在
- 根据弯曲拉应力公式可得 ( 为微面到中心面的距离, 公式见材料力学 P80)
- 由于主动轮 更小, 带轮最外侧 取最大, 因此主动轮最外侧上的弯曲应力最大
- 为了防止弯曲应力过大, 需要规定带轮的最小基准直径
- 最大应力
- 根据对三种应力的分析可得, 带轮的最大应力处为紧边开始进入小带轮处
- 满足
弹性滑动
- V 带在紧边上拉应力大, 弹性变形量大
- V 带在松边上拉应力较小, 弹性变形量小
- V 带进入主动轮中, 拉应力逐渐减小, 上面的微元在前进一段距离后, 向后收缩, 因此主动轮上
- V 带进入从动轮中, 拉应力逐渐增大, 上面的微元在前进一段距离后, 向前伸长, 因此从动轮上
- 由此导致 , 从而弹性滑动使带轮的传动比减小
- 定义弹性滑动率 体现弹性滑动的程度, 与 V 带的材料, 载荷有关
- 弹性滑动由 V 带本身性质导致, 无法避免, 不属于失效
失效形式
打滑
当圆周力 (即摩擦力) 超过摩擦极限 将发生打滑, 可得到不打滑条件 $$F=\frac{P}{v}\le F_{f lim}$$
疲劳破坏
V 带在变应力作用下发生疲劳破坏, 根据最大应力可得疲劳强度条件
单根 V 带的传动功率
根据两个约束条件, 可以得到在保证 V 带不失效的前提下, 单根 V 带能传动的功率为
计算单根 V 带的许用功率
直接计算得到的传动功率并不准确, 还需要进行修正才能得到其许用功率
| 参数名 | 字母代号 | 定义 |
|---|---|---|
| 单根 V 带基本额定功率 | 在特定实验条件下测得的额定功率 | |
| 基本额定功率增量 | 当 时, 额定功率存在一定增量 | |
| 包角系数 | 随包角增大而减小的修正系数 | |
| 带长系数 | 随带长增大的修正系数 |
影响因素分析
的影响因素分析
| 影响因素 | 影响效果 | 备注 |
|---|---|---|
| 初拉力 | 增大 可防止打滑, 但也将增大 V 带拉应力, 减小寿命 | |
| 小带轮包角 | 为了防止打滑, 要求 , 增大传动比 与减小中心距 均会导致 减小 | |
| 摩擦系数 | 需要选择合适的材料 |
设计参数
详细设计过程见 机械设计手册 第三卷 14-3
已知参数
| 参数名 | 字母代号 | 备注 |
|---|---|---|
| 名义传递功率 | ||
| 主动轮转速 | ||
| 传动比 | 通常 | |
| 工况系数 | 可得到计算功率 |
设计过程
| 参数名 | 字母代号 | 类型 | 备注 |
|---|---|---|---|
| V 带型号 | 无 | 标准值 | 通过 与 查询手册得到 |
| 主动带轮基准直径 | 系列标准值 | 为了防止弯曲应力过大, 对于各型号带轮, 存在 | |
| 从动带轮基准直径 | 计算值 | 通过计算值查找相近的标准值 | |
| 带速 | 验算值 | 过大将使离心拉应力过大, 过小则要求更高的有效拉应力 , 使带数增多 | |
| 初选中心距 | 选用计算值 | 中心距过大, 传动尺寸大, 但可以增加疲劳寿命, 增大包角; 此中心距是为了确定 | |
| 初选带长 | 计算值 | ||
| 基准长度 | 标准值 | 根据计算的到的带长, 从标准中选择相近值 | |
| 实际中心距 | 计算值 | 需要取整数 | |
| 小带轮包角 | 验算值 | 通常 , 因此仅验算 | |
| 带根数 | 验算值 | 当带数过多时, 将导致各根带受力不均, 需要改用带型或增大基准直径 | |
| 初拉力 | 计算值 | 初拉力过小容易出现打滑, 过大将降低轴与 V 带的寿命 | |
| 轴压力 | 计算值 | 用于轴的设计 |
常用设计
传动特点
- V 带轮主要用于高速级, 即电机输出与减速机输入之间的传动
- V 带轮存在弹性, 可以吸振, 缓冲, 减小噪声使传动平稳
- V 带存在打滑, 可以作为过载保护
- V 带需要张紧, 对轴施加了额外的轴向力
- 由于弹性滑动, 带传动不存在稳定的传动比
设计注意
- 根据 V 带的传动特点, 规定小带轮为主动轮, 大带轮为从动轮
- 由于重力作用, V 带会在重力的作用下下垂, 且松边下垂量大于紧边, 为了增大 V 带与带轮的接触 (即包角), 防止打滑, 紧边必须在下, 松边在上
链传动设计
设计分析
几何分析
链节几何尺寸
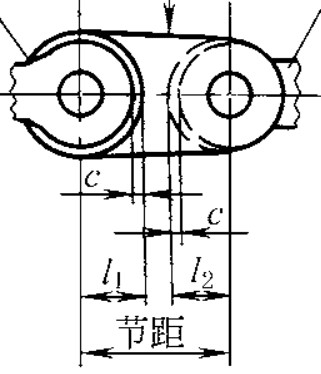
| 参数名 | 字母代号 | 定义 |
|---|---|---|
| 节距 | 单个链节上两个轴之间的距离, 节距决定了链节的大小, 因此大节距下, 链传动的承载能力更强 | |
| 链节数 | 链条上链节的个数, 通常为偶数, 使链能够首尾连接 | |
| 链排数 |
链轮几何尺寸
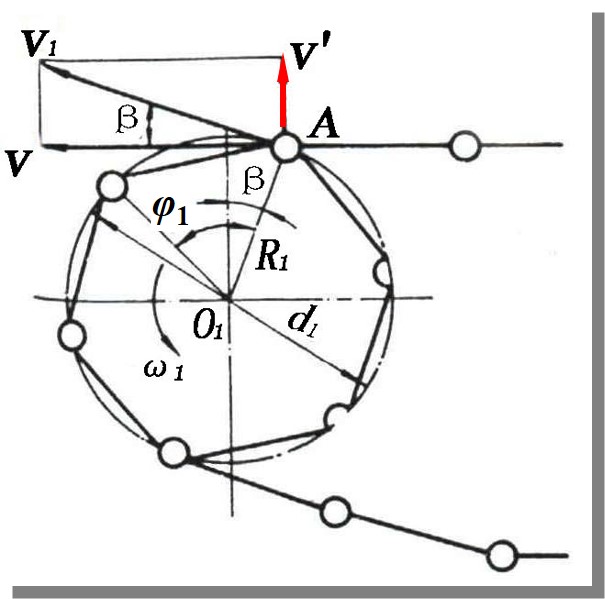
根据链条的特点, 链节在链轮上构成一个正多边形, 其中节距为多边形的边长, 链节的销钉为多边形的顶点
| 参数名 | 字母代号 | 定义 |
|---|---|---|
| 齿数 | 链轮上的齿数 | |
| 链节中心角 | 定义多边形的边长对应中心的角度为链节中心角, 即 | |
| 主动链轮转角 | 随链轮运动变化 | |
| 从动链轮转角 | 随链轮运动变化 | |
| 节圆半径 | 认为多边形顶点与中心的连线为链轮的节圆, 满足 |
基本运动分析
- 根据链轮的几何特点, 可得链轮上的链条以多边形分布, 因此链轮转动一圈, 相当于链条在此多边形上移动, 因此链条平均速度 ( 为链轮转速)
- 认为链传动的平均传动比满足 (与节圆直径无关)
主动轮运动分析

对于主动轮, 链节上的销钉在轮齿的带动下同步运动, 因此为匀速运动, 满足
假设链条有一边始终水平, 此时可将链条速度分解水平分量与垂直分量, 其中水平分量即链条速度, 满足
而竖直分量则反映了链节在链轮上跳动, 满足
可得链条的速度周期性变化, 并且在链轮上周期性跳动, 称为多边形效应
从动轮运动分析
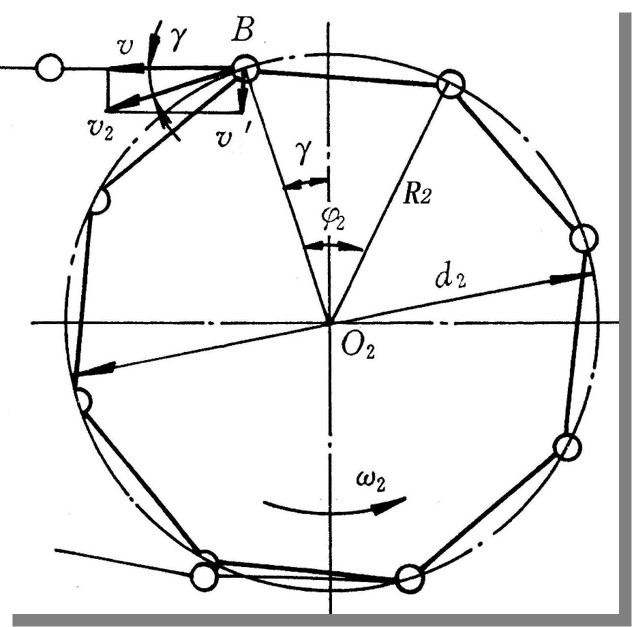
- 根据链节速度也可以计算出从动轮上销钉的转速, 此时该速度周期性变化
- 由此可得链传动的瞬时传动比不恒定
- 仅当 是, 瞬时传动比恒定, 但仍存在跳动
载荷分析
- 由于链速周期性变化, 因此加速度不为零将产生惯性力
- 加速度同样为周期性变化, 满足
- 因此当 为最大值时, 加速度达到最大值
影响因素分析
传动的均匀性
| 影响因素 | 影响效果 | 备注 |
|---|---|---|
| 齿数 | 增大齿数, 可以减小中心角 , 使速度变化范围减小, 从而减小运动的不均匀性 | |
| 节距 | 增大节距, 将增大链轮的尺寸, 相同转速下, 链条速度更高, 导致运动的不均匀性与动载荷大小增大 |
- 在高速重载时, 大节距会导致动载荷冲击大, 因此要选用小节距多排链, 通过增加链排数达到承载能力要求
- 在低速重载时, 动载荷冲击小, 为了节约成本, 要选用大节距少排链
设计参数
详细设计过程见 机械设计手册 第三卷 14-98
已知参数
| 参数名 | 字母代号 | 备注 |
|---|---|---|
| 名义传递功率 | ||
| 主动轮转速 | ||
| 传动比 | 通常 | |
| 工况系数 | 可得到计算功率 |
设计过程
| 参数名 | 字母代号 | 类型 | 备注 |
|---|---|---|---|
| 齿数 | 选用值 奇数 | 由于链节数为偶数, 为了使每个齿均匀磨损, 因此使用奇数齿数, 需要根据传动比选用 | |
| 额定功率 | 计算值 | 以 为约束条件, 选择有关参数时, 将同时确定排数 | |
| 链排数 | 选用值 | ||
| 型号/节距 | 选用标准值 | 不同型号的节距不同, 需要根据 与 选择 | |
| 初定中心距 | 选用计算值 | ||
| 带长 | 计算值 | 用于确定链节数 | |
| 链节数 | 计算值 | 通过 得到, 通常需要取整, 并且使用偶数 | |
| 实际中心距 | 计算值 | 通过 计算得到的中心距 | |
| 安装中心距 | 计算值 | 为了保证链条垂直, 且链条不需要预紧, 因此安装中心距通常小于计算得到的中心距 |
常用设计
传动特点
- 链传动中, 由于存在多边形效应, 传动不平稳, 瞬时传动比变化, 振动与噪声大
- 由于存在动载荷, 仅适用于低速传动
常用设计
- 链传动中也存在紧边与松边, 为了易于脱开链节, 要求松边在下, 紧边在上, 防止链条与链节过多接触
- 通常齿数设计为奇数, 链节数设计为偶数