平面四杆机构
大约 11 分钟
平面四杆机构
平面四杆机构的基础
四杆机构的结构
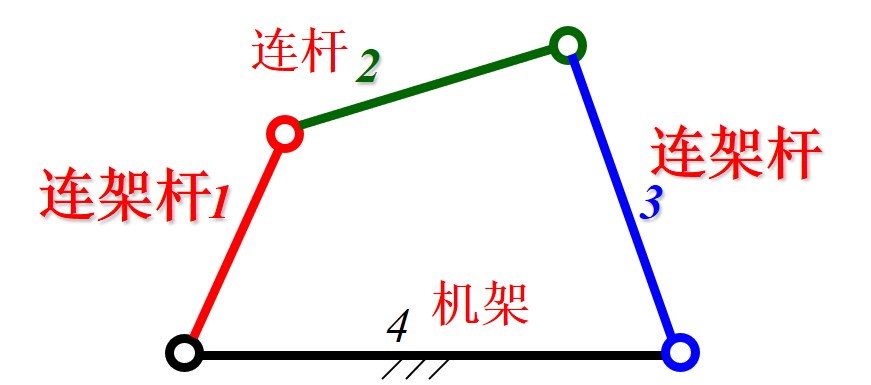
- 固定的杆 (通常为两固定铰链的连线) 为机架
- 与机架相连的杆为连架杆, 必定做圆周运动, 根据圆周运动是否完整又分为曲柄 (可以做完整的圆周运动) 与摇杆
- 与机架相对的杆为连杆, 连杆的运动规律通常比较复杂
机构的演化
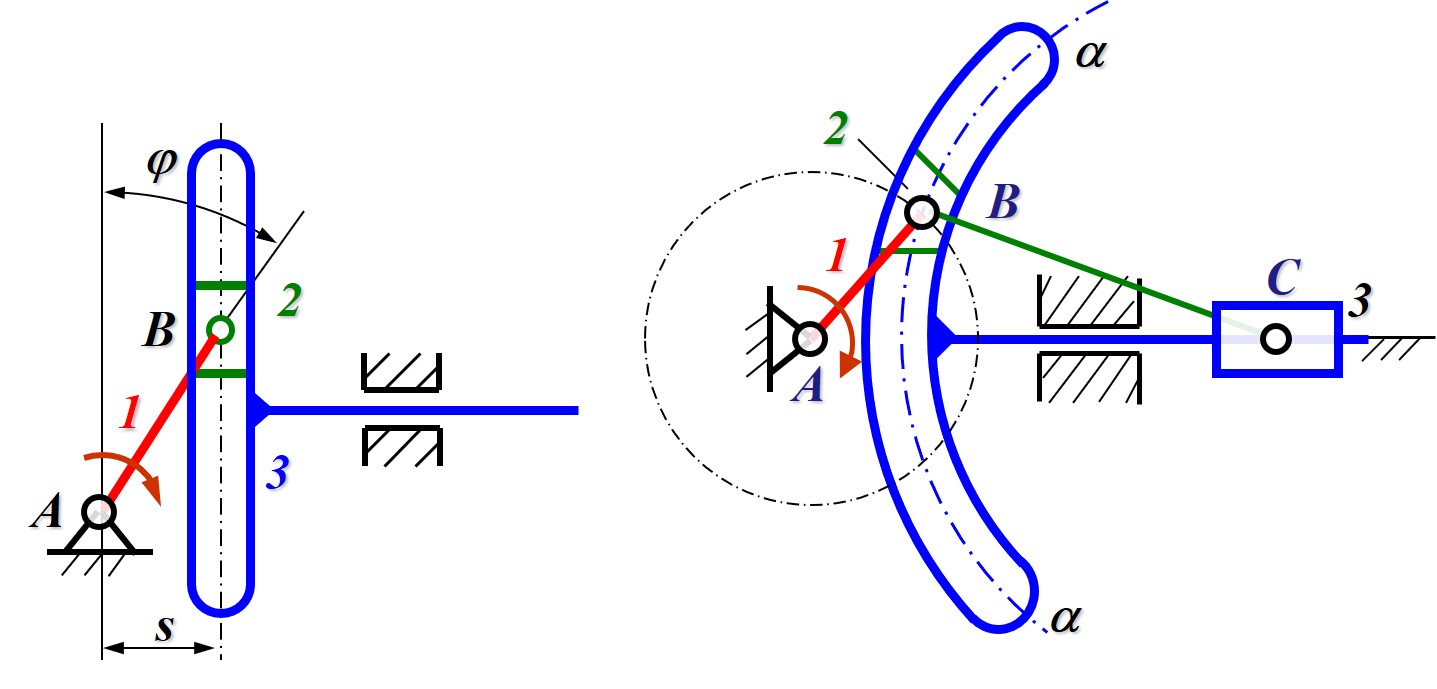
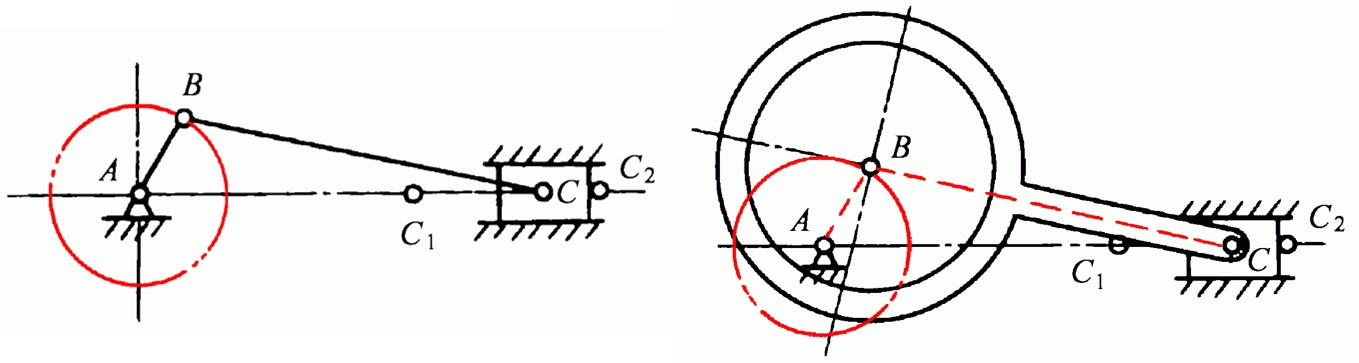
- 对于确定轨迹的摇杆, 可用一段圆弧导轨代替摇杆
- 当圆弧圆心位于无限远时, 圆弧变为直线, 圆心所在的转动副变为移动副
- 对于杆长过短时, 使用偏心圆代替杆 (注意分析自由度时应使用连杆替换偏心圆)
平面四杆机构的特性
平面四杆机构存在条件
- 为了使平面四杆机构中的杆件能够连接为一个封闭图形, 需要满足, 即最长杆长度小于其他杆长之和
- 仅当满足此条件时平面四杆机构才能存在, 因此通常平面四杆机构中杆件的长度不能无限长
曲柄存在条件
- 杆长和条件 最短杆 , 最长杆 长度之和小于或等于另外两杆
- 曲柄位置条件 在满足杆长和条件后, 当最短杆不为连杆时, 则存在曲柄
普通平面四杆机构的分类
- 曲柄摇杆机构 最短杆为连架杆, 此时最短杆即曲柄
- 双曲柄机构 最短杆为机架, 此时两连架杆均为曲柄
- 双摇杆机构 当不满足杆长和条件或最短杆为连杆时, 没有曲柄
曲柄滑块机构的曲柄条件
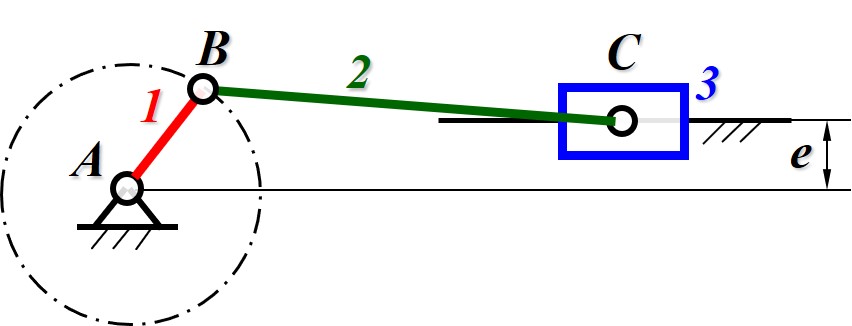
- 定义曲柄长 , 连杆长 , 偏置 , 假设轨道无限长
- 曲柄的轨迹为一条圆形, 即圆形上每一点均能通过连杆到达轨道
- 可得圆形轨迹上到轨道最远距离即
- 因此存在曲柄的条件为
导杆机构的曲柄条件
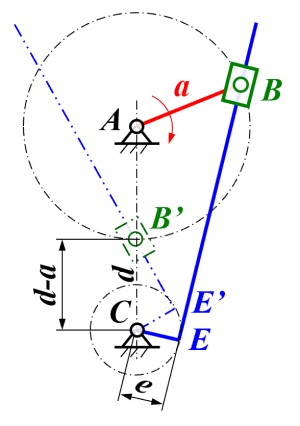
- 定义曲柄长 , 导杆偏置 , 曲柄与摆杆铰链距离 , 假设轨道无限长
- 由于滑块最低不能到偏置区域, 因此可得曲柄条件为
- 当曲柄足够长时, 滑块的轨迹完全包含了偏置区域, 则导杆也可以做圆周运动, 此时有
输出件的急回特性
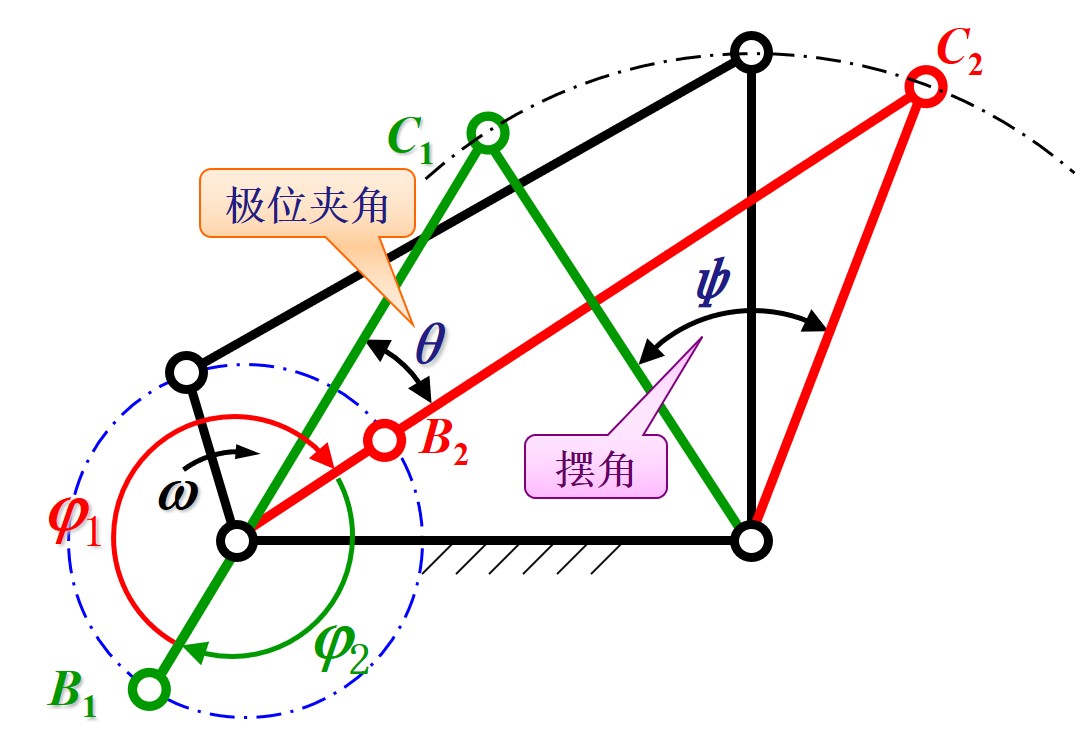
- 对于曲柄摇杆机构, 将曲柄作为输入件, 摇杆作为输出件
- 此时, 曲柄做等角速度的圆周运动, 而摇杆则做往复运动
- 由于摇杆的两个极限位置对应的曲柄转角不相同, 因此摇杆的往复两个行程的速度并不相同, 称为急回特性
- 通常工作行程 要求速度慢以输出大功率, 空回行程 要求速度快以迅速回复, 通过改变曲柄转动方向, 可改变两个行程的方向
- 当曲柄与连杆共线时, 摇杆达到极限位置, 由于曲柄与连杆存在重叠与分离两种共线状态, 因此共有两个极限位置; 取曲柄在这两个极限位置下的锐角为极位夹角
行程速度变化系数
- 通过引入行程速度变化系数 来表明急回特征
- 值为工作行程与空回行程下时间之比, 满足 (注意曲柄为匀角速度)
- 当行程速度变化系数 已知时, 可确定极位夹角
存在急回特性的条件
- 原动件等角速整周转动 (通常即曲柄)
- 输出件具有正、反行程的往复运动 (也可以是滑块的往复运动, 但不可是圆周运动)
- 极位夹角 (不能等于 , 因此无偏置曲柄滑块没有急回特性)
传动角与压力角
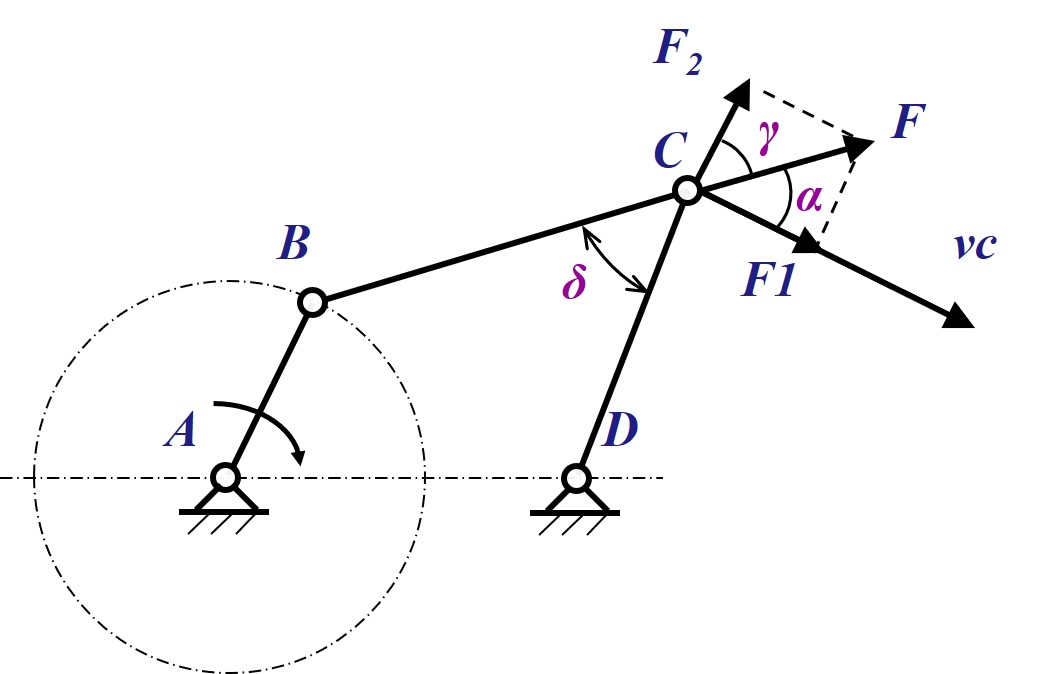
- 在不计惯性力与重力的条件下, 四杆机构中的杆件仅受来自铰链的力, 且均为二力杆
- 在曲柄摇杆机构中, 从动件摇杆受到来自连杆的驱动力
- 将 沿摇杆的运动方向 (即垂直于摇杆方向) 分解, 得到平行于速度的分量 与垂直于速度的分量
- 其中 做功, 不做功, 仅对摇杆产生压力, 因此 越大, 机构的传力效果越好
- 定义传动角 用于体现传动力 的大小, 传动角越大, 在传动力方向的分量越大, 满足 (注意传动角是压力与驱动力的夹角)
- 定义压力角 用于体现压力 的大小, 压力角越大, 在压力方向的分量越大, 满足 (注意压力角是传动力与驱动力的夹角)
- 压力角于传动角之间满足关系
- 注意压力角与传动角反映的是连杆与从动件之间关系, 因此对于同一机构, 从动件不同, 压力角与传动角不同
- 注意压力角与传动角的大小随机构运动状态改变, 通常校核最小传动角或最大压力角
- 通常要求机构在其工作行程中避开最大压力角所在位置,
曲柄摇杆机构的最大压力角
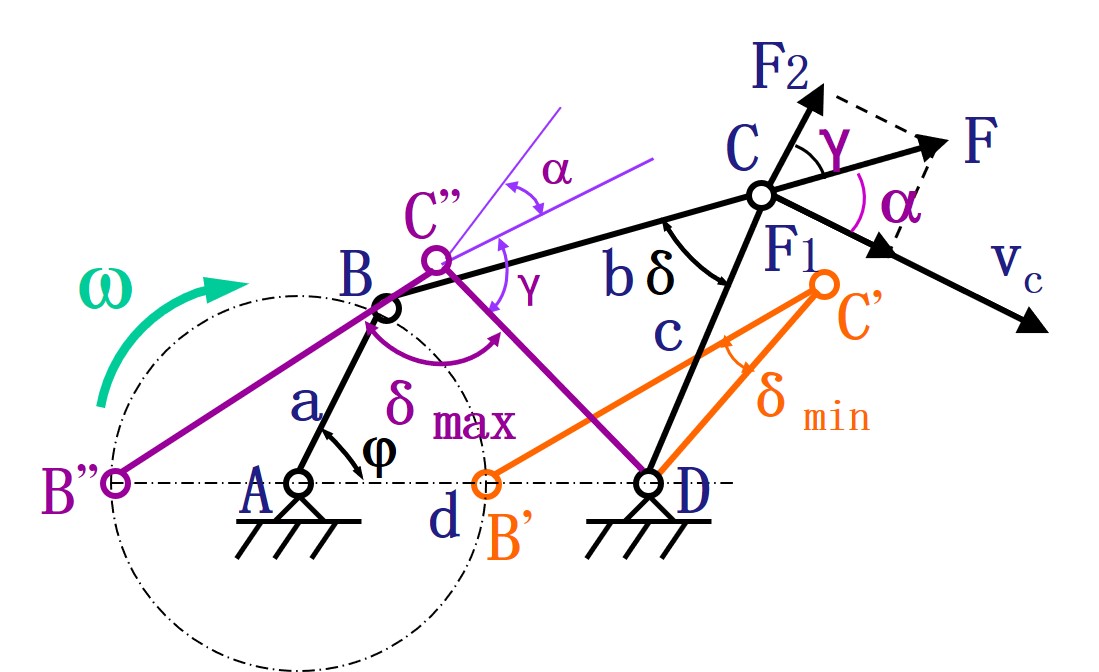
- 在曲柄连杆机构中, 以曲柄作为输入件时可得传动角 与连杆摇杆夹角 满足关系
- 当曲柄 与机架 不重叠平行时取得 (通过作图法得出)
- 当曲柄 与机架 重叠平行时取得 (通过作图法得出)
- 最小传动角满足
曲柄滑块机构的最大压力角
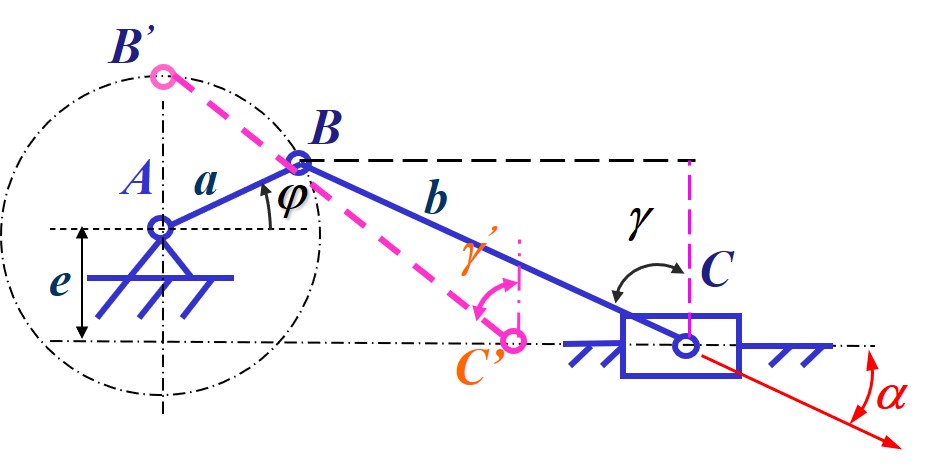
- 注意滑块的运动方向为导轨所在直线, 因此传动力的方向即导轨方向, 与驱动力的夹角即压力角
- 由于连杆长度不变, 因此当 距离导轨最远时, 取得最大压力角, 满足
异形机构的压力角
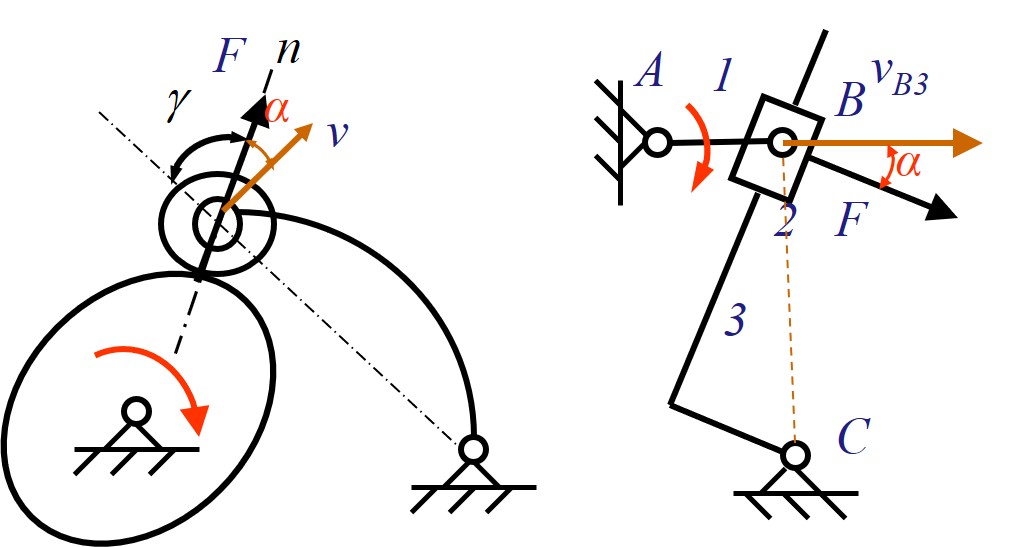
- 对于任意异形二力杆作为传动件时, 注意二力杆上的力始终沿两受力点所在直线, 与杆件形状无关
- 对于凸轮作为传动件时, 注意凸轮的驱动力方向为凸轮与滚子接触点的公法线
- 对于套筒为传动件时, 注意套筒仅能产生垂直于滑轨方向的力, 因此驱动力垂直于滑轨
- 当从动件与铰链连接时, 从动件绕固定铰链旋状, 因此速度方向为圆周轨迹的切线方向
- 当从动件为套筒时, 速度方向即导轨方向
死点
- 当传动角 时, 无论驱动力多大, 均不能使机构运动, 称为死点
- 死点通常出现在以摇杆为主动件, 曲柄或摇杆为从动件或平行四边形机构等情况 (脚踏缝纫机)
- 也可利用死点实现机构结构的固定等效果
设计平面四杆机构
几何法要求
- 使用几何法前必须指定比例尺 , 其中 为图上的尺寸, 为对应实际长度的尺寸
- 在确定比例尺后有长度比例 (注意与比例尺相反)
- 量取图上的长度, 得到实际长度, 有计算式
给定速度变化系数设计连杆机构
设计四杆机构
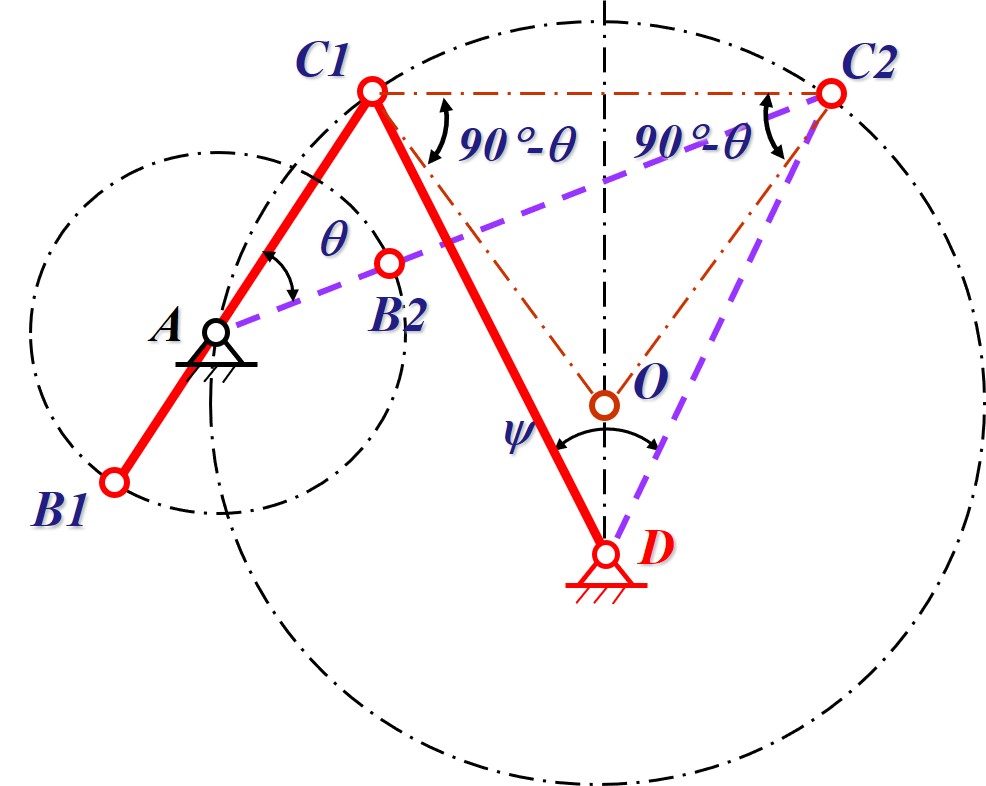
- 已知条件: 摇杆长度 , 摇杆摆角 , 行程速度变化系数
- 设计步骤
- 根据 计算出极位夹角
- 取任意一点作为固定铰链 , 根据摆角 与摇杆长度做等腰三角形即可确定摇杆的两个极限位置
- 极限位置与曲柄铰链 之间连线的夹角即极位夹角 , 根据圆心角定律, 假设 在一个辅助圆上, 根据圆心角定律, 弦 的圆心角为 , 因此以 为底边, 做底角为 的等腰三角形即可得到辅助圆圆心
- 做出辅助圆后, 曲柄铰链 可以是圆上任意一点, 具体根据额外的约束条件确定
- 得到 后, 将其与极限位置连线, 长度分别为 , 以此可解出四杆机构
设计曲柄滑块机构
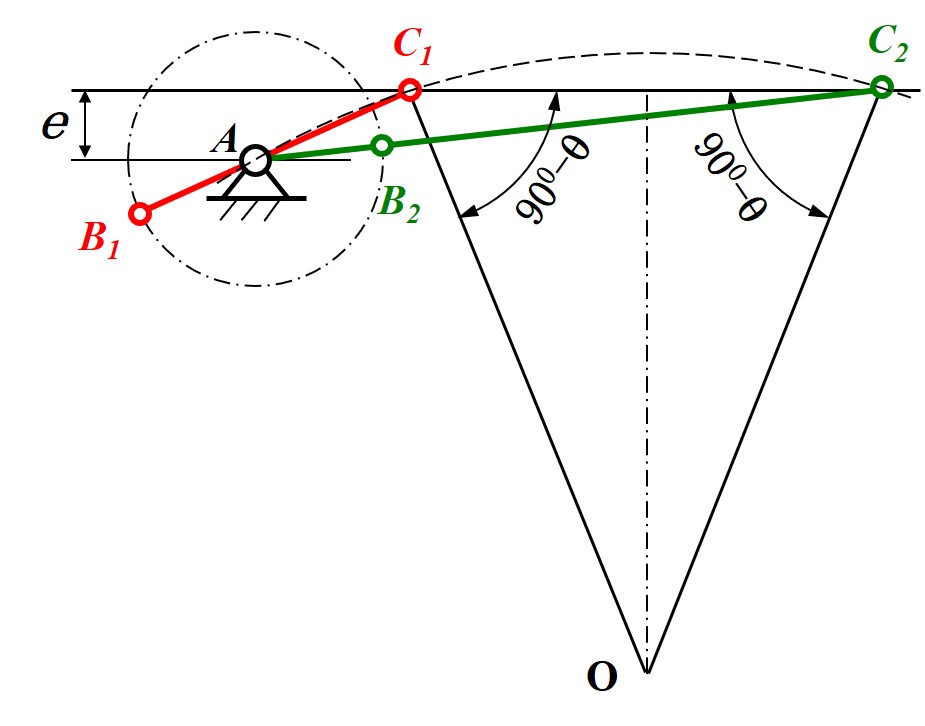
- 已知条件: 滑块移动的行程 (即极限位置距离), 曲柄铰链与导轨的偏距 , 行程速度变化系数
- 设计步骤
- 根据 计算出极位夹角
- 由于滑块移动的行程已知, 因此做线段 即可得到滑块的极限位置
- 使用与四杆机构同样方法做出辅助圆
- 根据偏距 , 做平行于 且距离为 的直线截取辅助圆可得到曲柄圆心 位置 (注意未说明时, 偏距可向上或向下取)
- 使用与四杆机构同样方法得到曲柄与连杆长度
设计曲柄摆杆机构
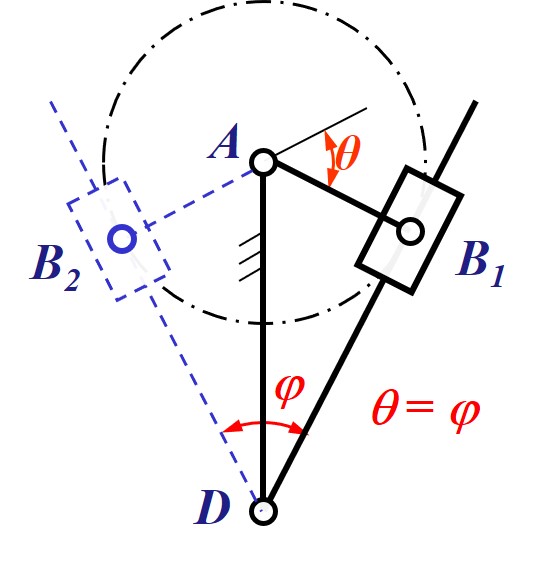
- 已知条件: 机架长度 , 行程速度变化系数
- 设计步骤
- 根据 计算出极位夹角
- 对于曲柄摆杆机构, 摆角与极位夹角相同, 有 , 因此可做出摆杆在极限位置的状态
- 以 为圆心做圆与极限位置摆杆相切, 圆的半径即曲柄长度
给定轨迹设计连杆机构
使用刚化反转法解决此类问题
已知条件
- 已知其中一个连架杆 的长度
- 已知机架为位置
- 对于点 在连杆 上 (注意连杆整体不做圆周运动) 或连架杆 上, 已知某时刻的 下, 的位置
推导条件
- 通过题目条件即可确定 点的位置, 而 点为待求点
- 点 与其所在的杆件组成一个三角形刚体, 因此 到杆上另外两点的距离始终不变
- 如果将待求杆件固定视为机架, 将机架视为活动部件, 此时 点的位置也将保持不变
设计步骤
- 画出各个状态下所有已知点的位置
- 刚化 所在的杆件
- 当 在 上, 则 到已知点 距离不变, 将图形整体旋转平移至与 对齐
- 当 在 上, 则 到已知机架端点 距离不变, 将图形旋转至于 对齐
- 找出刚化杆件的另一个固定支点
- 当 在 上, 则转换后的 点将绕刚化固定支点 做圆周运动, 因此通过中垂线即可确定 的位置
- 当 在 上, 则转换后的 点将绕刚化固定支点 做圆周运动, 因此通过中垂线即可确定 的位置
- 量取各根杆的长度即可得到目标四杆机构
其他条件下的刚化反转法
- 对于给出多状态, 已知四杆机构中的三个点 , 求非机架点 位置的题目均可采用刚化反转法
- 刚化反转的目标均为 所在的杆, 且已知杆的转动角度等大致状态以反转
- 通过反转后的一个点绕 转动的特点, 通过中垂线求出