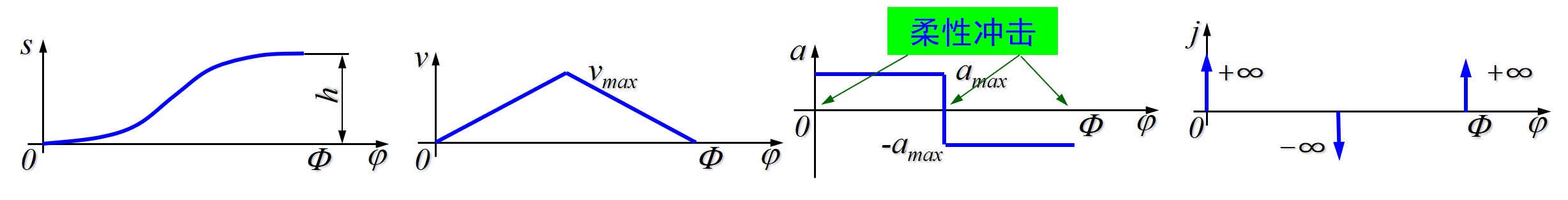凸轮

凸轮传动特点

1. 凸轮设计简单, 结构紧凑, 多用于自动与半自动机械
2. 凸轮机构为高副, 压力较大容易磨损, 一般仅能传递运动

凸轮运动规律

凸轮基本运动规律

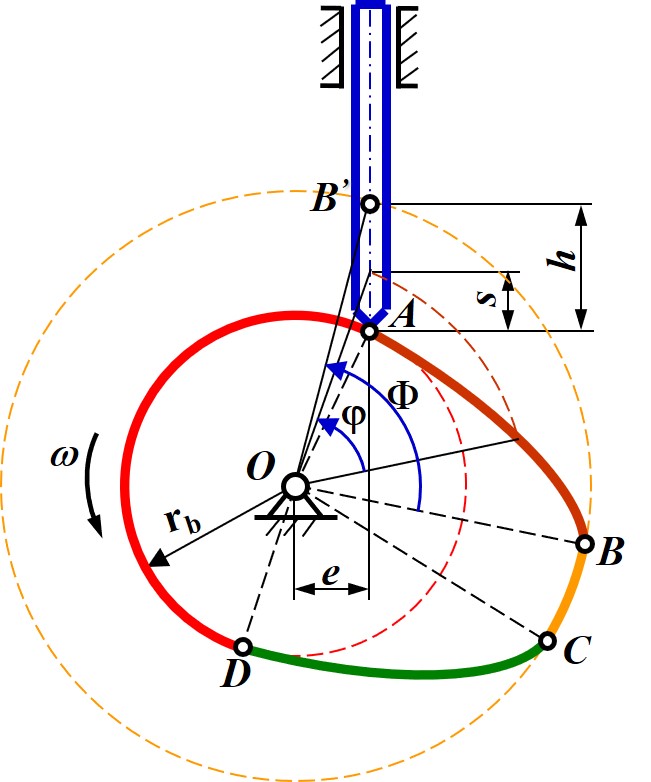
• 将滚子在凸轮基圆上的位置作为基准, 凸轮在转动过程中, 滚子的位移称为推程 $s$
• 定义凸轮相对初始位置转动的角度为推程角, 满足 $\varphi=\angle BOB'$ (几何证明见后)
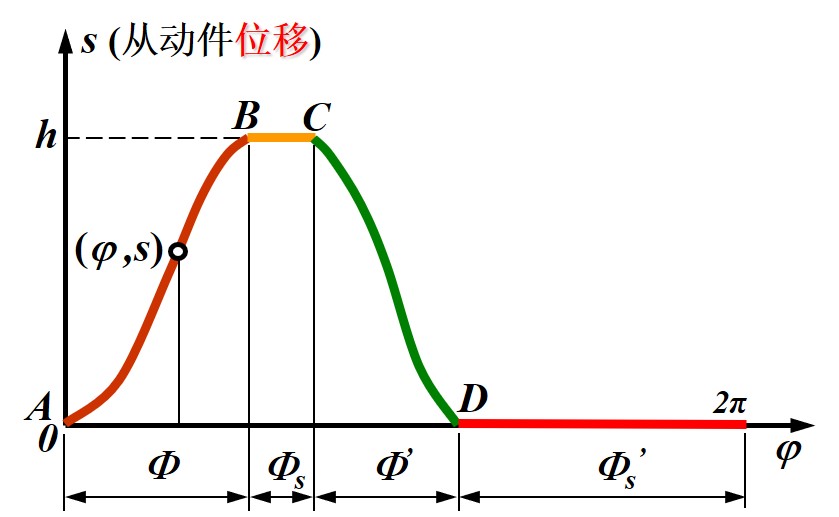
• 通过函数 $s=f(\varphi)$ 来表示凸轮的运动规律, 将 $s$ 上升段称为推程, 下降段称为回程, 主要研究这两端上凸轮的运动规律, 推程不变部分则称为休止
• 在休止处或推/回程开始处, $f(\varphi)=0/h$, 为常数
• 由于凸轮匀速转动 ($\omega=\frac{d\varphi}{dt}$), 因此滚子的有关运动量可以表示为 (不是直接等于 $f(\varphi)$ 的导数, 还有系数 $\omega^n$ 不能漏)

$$v=\frac{ds}{dt}=\omega\frac{ds}{d\varphi},\;a=\frac{dv}{dt}=\omega^2\frac{d^2s}{d\varphi^2},\;j=\frac{da}{dt}=\omega^3\frac{d^3s}{d\varphi^3}$$

其中 $j$ 为跃动度

• 在休止处或推/回程开始处, $f(\varphi)$ 的任意阶导数均为 $0$, 因此对于大部分运动规律, 在推/回程开始处的 $v,a,j$ 等可能发生突变
• 对于不同运动规律中系数的取值, 可通过以下条件求出推程下的状态

$$\begin{split} &f(0)=0\\ &f(\Phi)=h\\ &\frac{ds^i}{d^i\varphi}\bigg|_{\varphi=0/\Phi}=0 (i=1,2,\dots,n) \end{split}$$

• 对于推程状态
  • $n$ 的取值根据运动规律中第一个没有在起止位置发生突变的运动特征决定, 从小到大求导, 可能提前求出参数
  • 若回程的运动规律与推程一致, 则可带入 $\varphi'=(\Phi-\varphi)$ 变换得到, 或修改初值条件
  • 对于混合规律的运动, 则还有运动特征连续条件, 即各个运动特征需要连续 (可能出现冲激函数)
• 通常要求从动件的各项运动特征尽可能小且没有突变, 以此作为评价运动规律的基本标准

多项式运动规律

等速运动

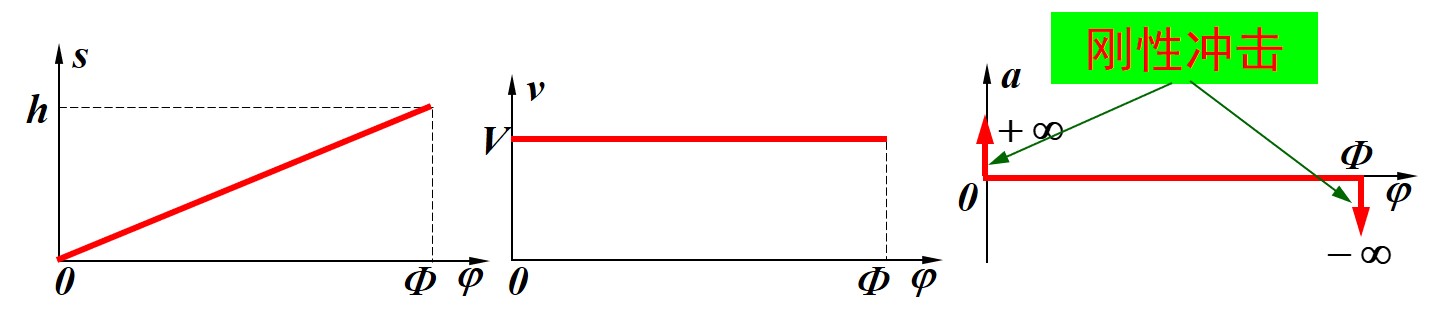
等速运动下, 运动规律满足形式

$$f(\varphi)=c_0+c_1\varphi$$

因此图像为一条直线

1. 此时速度则为常数 $v=\omega c_1$
2. 在运动开始 / 结束时, 速度从 $0$ 突变到 $v$, 因此加速度 $a$ 在这些时刻存在冲激函数, 称为刚性冲击, 滚子将受到巨大的惯性力, 因此仅能用于极低速场合

等加速等减速运动

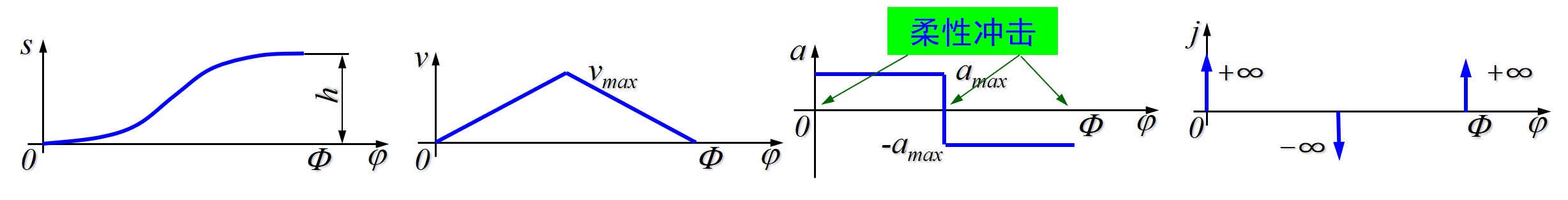
等加速度运动下, 运动规律满足

$$f(\varphi)=c_0+c_1\varphi+c_2\varphi^2$$

1. 注意存在匀加速与匀减速两个部分, 因此 $s,v$ 为分段函数, 并且通常关于 $\varphi=\Phi/2$ 处对称 / 中心对称 ($f(\Phi/2)=h/2,f'(\Phi/2)=\omega v_{max}$)
2. 等减速部分 (后半段) 可通过带入 $f(\varphi)=h/2-s(\Phi-\varphi)$
3. 此时速度为两段折线, 并且没有在起止处发生突变
4. 此时加速度发生共三次突变, 但没有冲激函数
5. 在运动中由于跃动度 $j$ 中存在冲激函数, 称为柔性冲击, 在低速下影响小, 但在高速下仍有较大的动载荷

三角函数式运动规律

余弦加速度运动

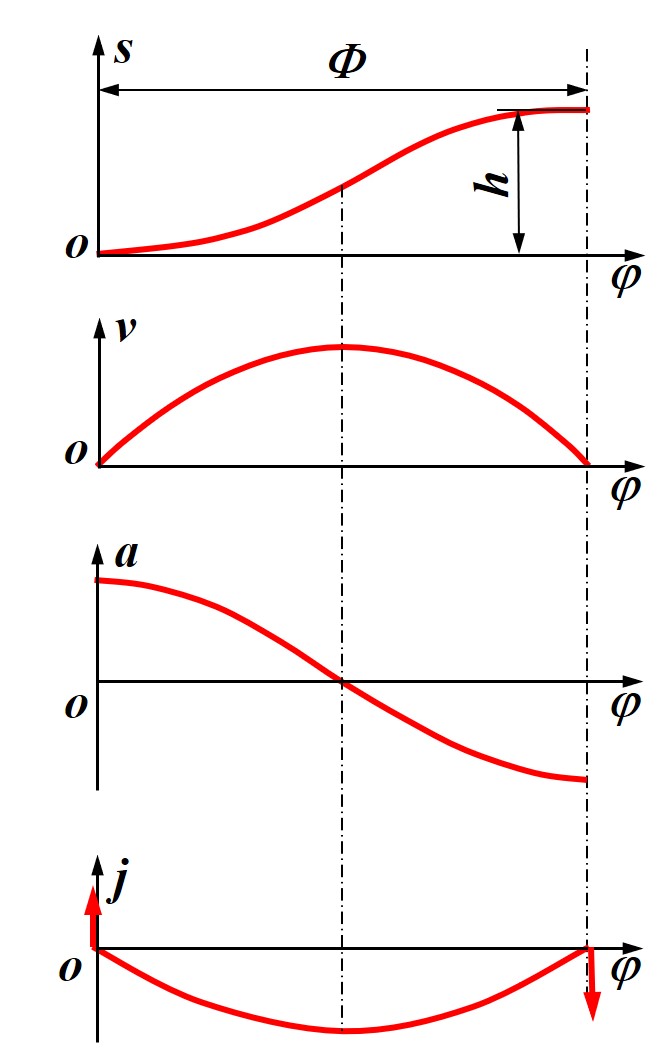
由名称可得, 此运动规律下加速度为一个余弦函数, 并在 $\Phi$ 内完成半个周期

$$a=c_1\cos(\frac{\pi}{\Phi}\varphi)$$

通过积分可得到运动规律的表达式满足

$$s=c_0\cos(\frac{\pi}{\Phi}\varphi)+c_1\varphi+c_2$$

注意到余弦加速度在开始与结束处依然存在突变, 因此跃动度中存在冲激函数, 存在柔性冲击

正弦加速度运动

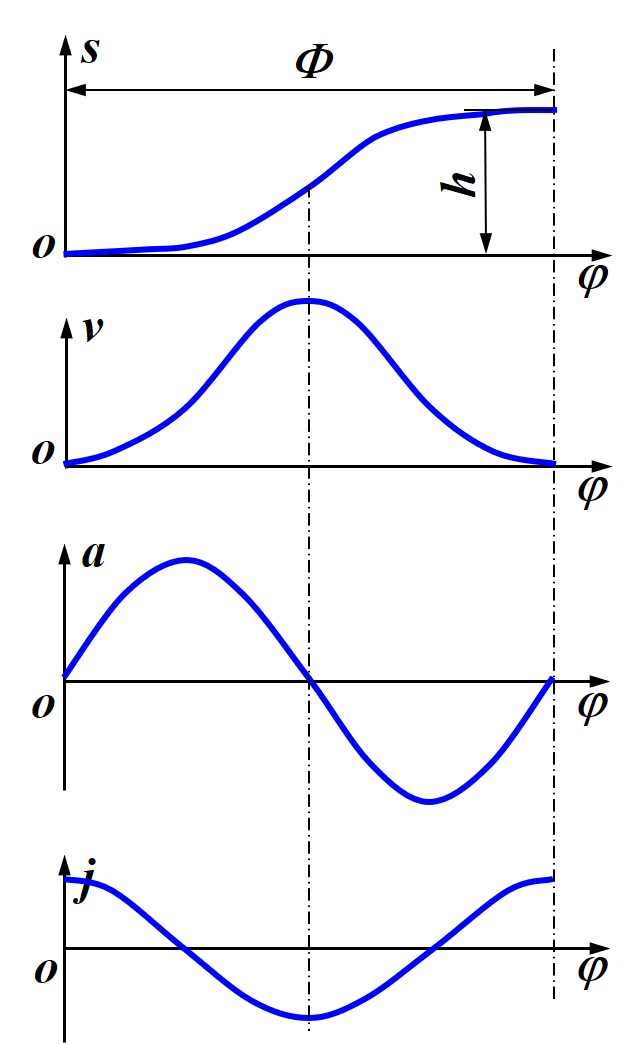
由名称可得, 此运动规律下加速度为一个正弦函数, 并在 $\Phi$ 内完成一个完整周期

$$a=c_1\cos(\frac{2\pi}{\Phi}\varphi)$$

通过积分可得到运动规律的表达式满足

$$s=c_0\sin(\frac{\pi}{\Phi}\varphi)+c_1\varphi+c_2$$

注意到正弦加速度在开始与结束处为 $0$, 因此跃动度没有冲激函数, 不存在刚性冲击与柔性冲击

凸轮结构设计

移动从动件凸轮的相对运动瞬心

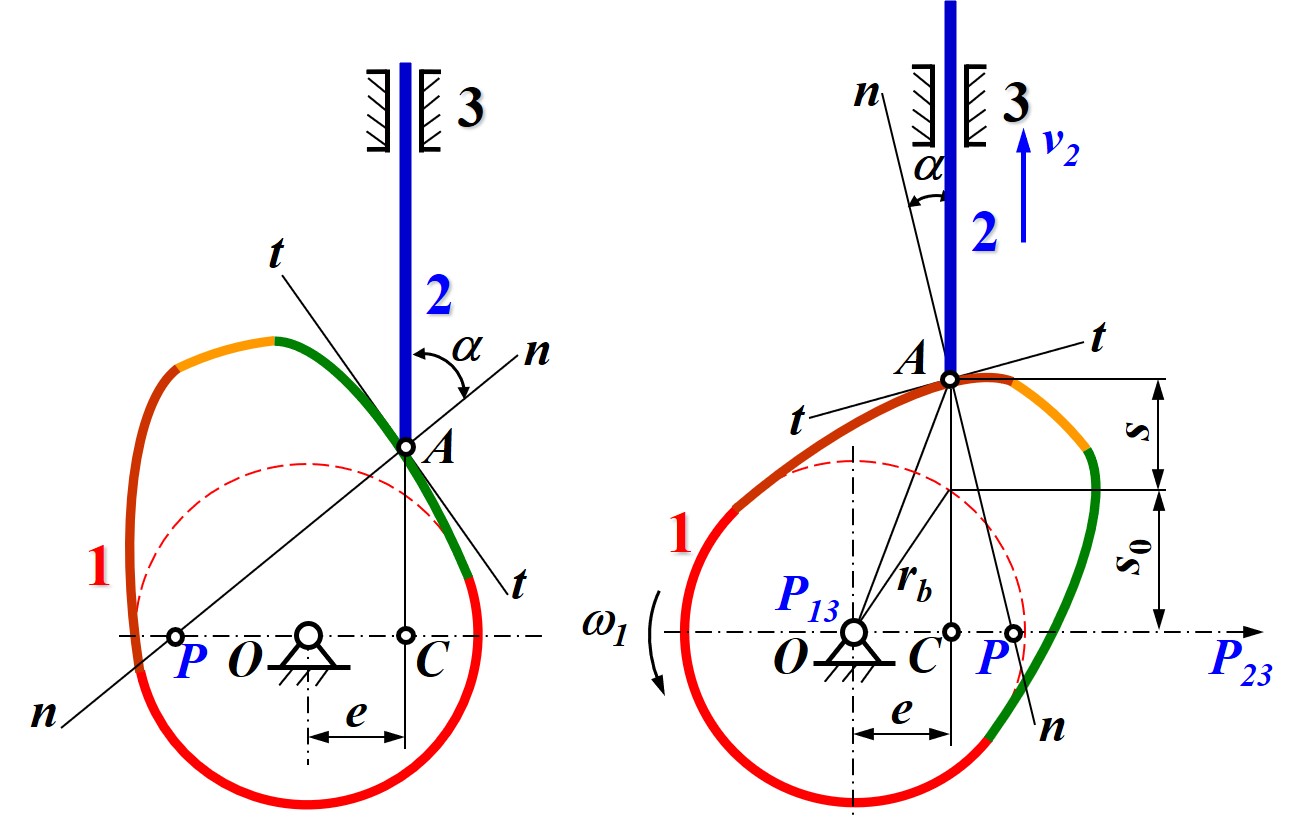
1. 根据三心定律, 可以确定推杆与凸轮相对运动的瞬心为接触点 $A$ 的法线 $n-n$ 与过铰链 $O$ 且垂直于推杆的轴线的交点 $P$
2. 在速度瞬心 $P$ 上两机构的运动速度相同, 且推杆以 $v_2$ 垂直运动, 凸轮以 $\omega_1$ 绕 $O$ 转动, 因此可得出 $OP\omega_1=v_2$
3. 由于推杆的运动方向垂直, 凸轮通过接触力驱动推杆, 驱动力沿接触点的法线方向, 因此可做出压力角 $\alpha$ 即接触点法线与推杆运动方向的夹角, 且有 $\angle CAP=\alpha$
4. 由于 $OP$ 长度已知, 且其他长度几何关系确定, 即可通过三角函数得到压力角的表达式

移动从动件凸轮偏置方位对压力角的影响

1. 以减小从动件工作行程时的最大压力角为原则选择偏置
2. 由于 $\angle CAP=\alpha$, 因此当偏置点 $C$ 与瞬心 $P$ 同侧时, 压力角较小
3. 若不好判断 $C$ 与 $P$ 相对于 $O$ 的位置, 则可以寻找最大 / 最小压力角下的状态, 并在工作行程避开 / 通过这些状态
4. 并且有几何特征可得, 偏置越大, 两侧压力角相差越大, 因此偏置也不可取得过大
5. 通过控制凸轮转向或偏置方位来保证

移动从动件凸轮的其他参数对运动的影响

1. 增大基圆半径可以减小压力角, 但增大机构尺寸
2. 当凸轮得推程大时, 压力角将减小
3. 当推杆速度大时, 压力角将增大

摆动从动件凸轮的压力角特点

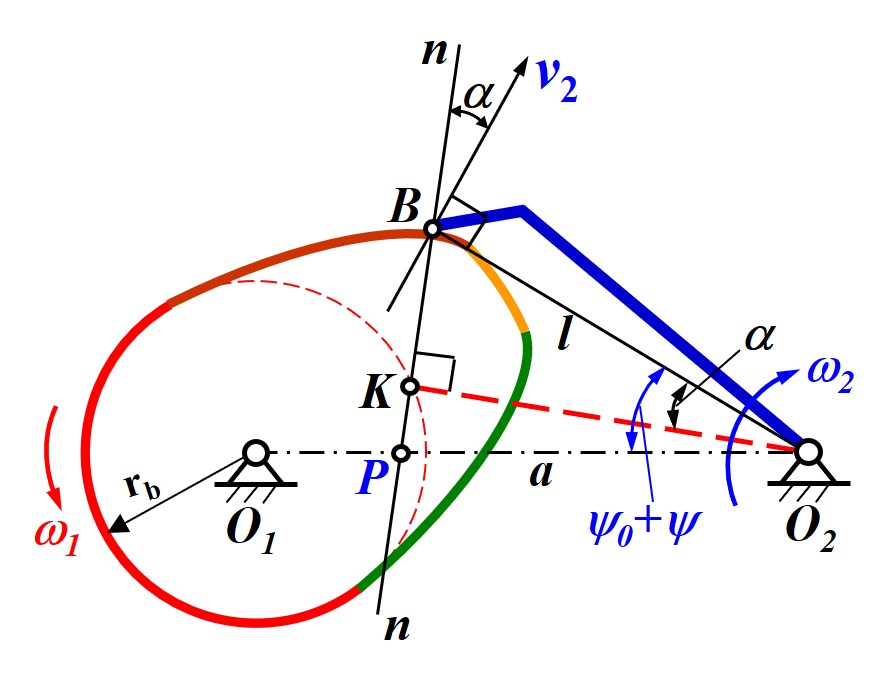
1. 对于摆动从动件, 当凸轮角速度 $\omega_1$ 与摆动件角速度 $\omega_2$ 异向时压力角较小, 相反则较大, 以相同原则确定凸轮转向
2. 对于任意形状的摆件, 等效为连接接触点与转动铰链的杆

凸轮轮廓确定

尖顶从动件凸轮轮廓设计

基本理论

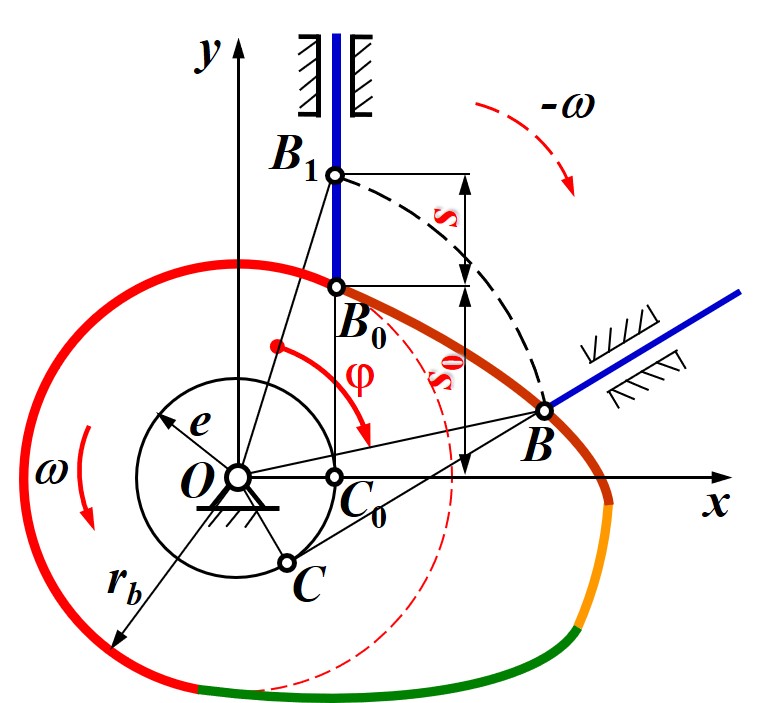
1. 通过固定凸轮, 而是旋转从动件来确定凸轮轮廓, 注意此时从动件的旋转方向应与凸轮转动方向相反
2. 在固定凸轮旋转从动件时, 从动件与旋转中心的偏置关系始终不变, 因此从动件所在直线始终切于直径为偏置 $e$ 的圆周
3. 由相切点 $C$, 圆心 $O$ 与从动件上一点 $B$ 组成三角形, 从动件旋转的本质为此三角形的旋转
4. 由于旋转的特点, 因此角 $\angle B_1OB$ 即推程角 $\varphi$
5. 因此, 从基圆上的运动开始点作为 $CO$ 起始边, 根据推程 $s(\varphi)$ 确定 $B$ 位置, 反向旋转 $\varphi$ 即可得到凸轮轮廓
6. 对于刚化反转法, 重点即三角形 $\Delta OCB$ 的旋转
   1. $O$ 点即凸轮旋转中心
   2. $C$ 点即偏置, 始终保持 $OC=e$
   3. $B$ 点即理论轮廓上的点
   4. 三角形中 $\angle OCB=90^\circ$, 且 $BC$ 始终为推杆的移动方向, 并且推杆的移动需要通过比较 $BC$ 的长度来反映
   5. 由于三角形总是绕 $O$ 旋转, 因此有角度关系 $\angle B_1OB_2=\angle C_1OC_2$
   6. 对于已知状态 $1$ 与理论轮廓上一点 $B_2$, 可先求出 $\angle B_1OB_2$, 再旋转 $OC_2$ 相同角度确定 $C_2$
   7. 对于已知初始状态 $1$ 与推程 $s$, 推程角 $\varphi$, 可在初始状态的 $C_0B_0$ 上取出 $B_1'$, 旋状 $OB_1'$ 得到 $B_1$

设计过程

• 求出从动件的初始位置 $B_0$ , 注意在有偏置的情况下, 从动件接触点到轴线的距离不是基圆半径, 因此需要求出接触点到轴线的距离 $s_0=C_0B_0$
• 推程 $s(\varphi)$ 即从动件的位移, 因此在初始位置向上取 $s(\varphi)$ 得到 $B_1$
• 对于几何法, 将边 $OB_1$ 以角速度的反方向旋转 $\varphi$ 即可得到凸轮在推程角为 $\varphi$ 处的轮廓
• 对于解析法, 则需要以 $O$ 点建立坐标系, 并对点 $B_1$ 进行如下旋转变化, 得到 $B$ 坐标

$$\begin{bmatrix} x_B \\ y_B \\ \end{bmatrix}=\begin{bmatrix} \cos(-\varphi)&-\sin(-\varphi) \\ \sin(-\varphi)&\cos(-\varphi) \\ \end{bmatrix}\cdot\begin{bmatrix} x_{B_1} \\ y_{B_1} \\ \end{bmatrix}$$

其中

$$\begin{bmatrix} x_{B_1} \\ y_{B_1} \\ \end{bmatrix}=\begin{bmatrix} e \\ s_0+s \\ \end{bmatrix}$$

尖顶摆动从动件凸轮轮廓设计

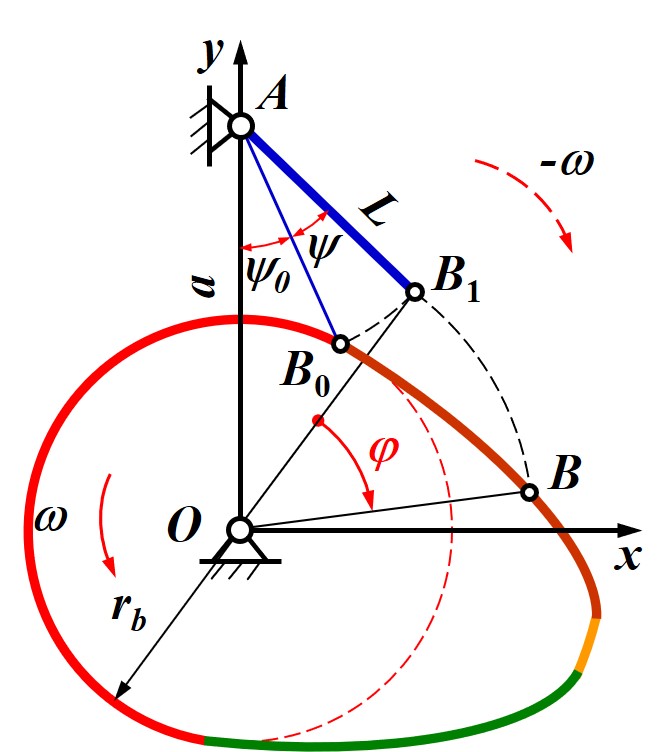
1. 注意摆动从动件初始状态下, 接触点在基圆上的行程开始点, 摆杆旋转圆心还需要通过摆杆长度确定
2. 采用固定凸轮旋转从动件与旋转圆心的方法确定凸轮轮廓, 因此也需要反转, 此时旋转的三角形为 $\Delta AOB_1$
3. 首先依然要求出初始位置下的摆角 $\psi_0$ 并转动摆角 $\psi$ 得到 $B_1$
4. 将边 $OB_1$ 旋状 $\varphi$ 得到推程角为 $\varphi$ 下的轮廓

滚子凸轮轮廓设计

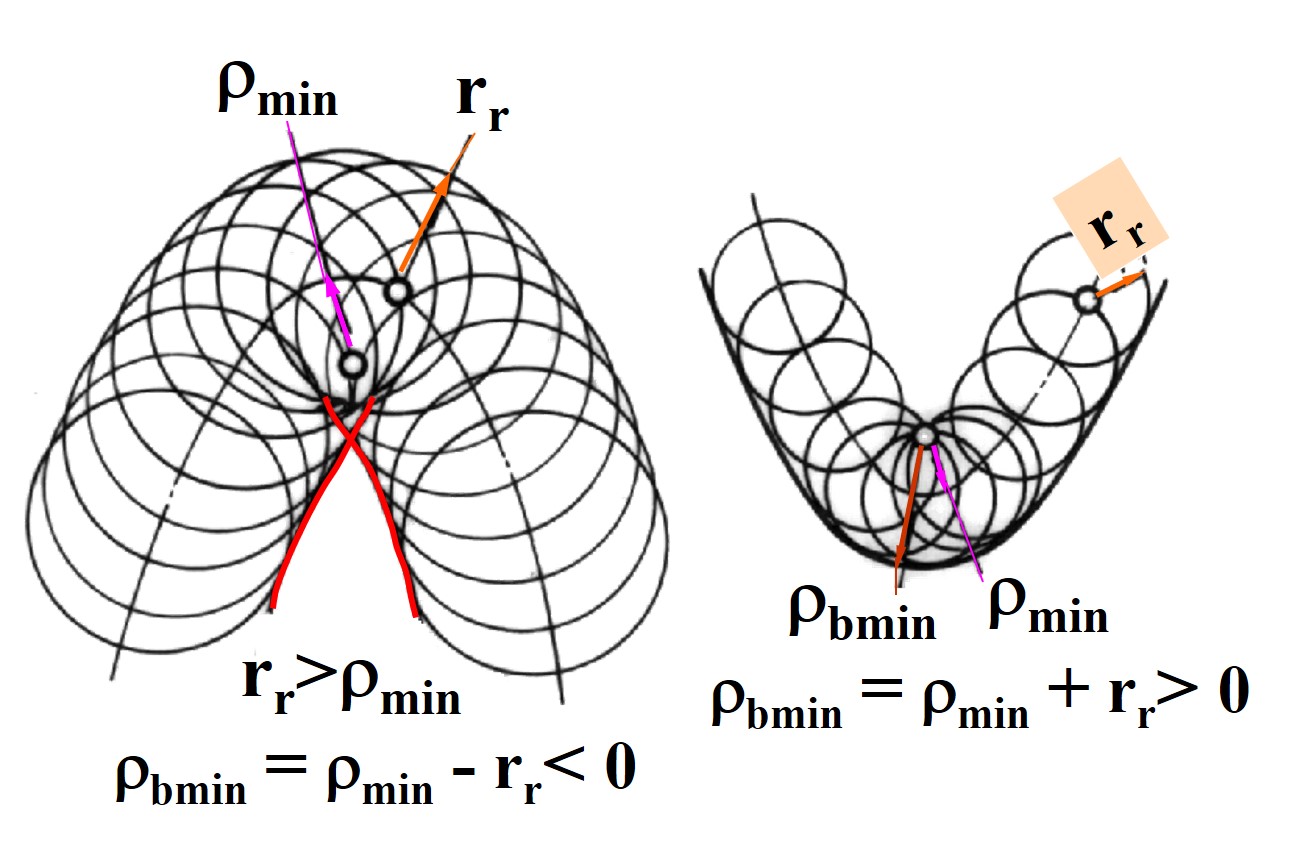
1. 对于存在滚子的情况, 对于几何法, 可直接令推程 $s'=s\pm r_r$, 得到近似轮廓线 (对于一般凸轮取 $-$, 外包凸轮则取 $+$)
2. 对于解析法, 需要先求出理论轮廓, 即滚子圆心的轨迹, 再根据法线方向移动 $r_r$ 得到实际轮廓
3. 定义滚子半径 $r_r$, 凸轮最小曲率半径 $\rho_{min}$
4. 对于外凸轮廓, 当 $r_r>\rho_{min}$, 轮廓将出现交叉

凸轮几何特点

偏置凸轮角位移

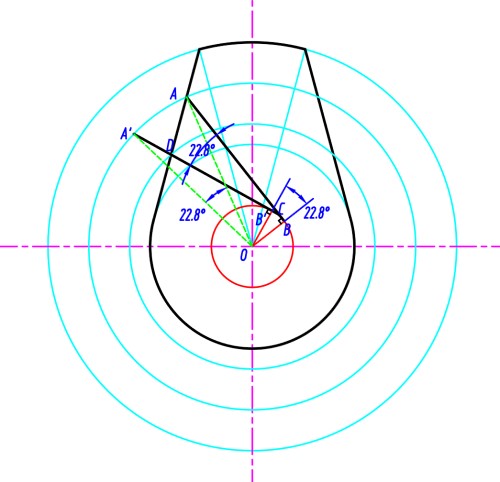
对于存在偏置的凸轮, 其角位移不是两次接触点 $A,D$ 与圆心 $O$ 的夹角, 而是新位置上旧接触点关于 $O$ 的圆投影 $A'$ 与旧接触点 $A$ 关于圆心 $O$ 的夹角

几何证明

1. 假设从动件运动, 主动件凸轮静止, 根据偏置不变, 可得从动件为以偏置 $e$ 为半径的圆的切线
2. 因此对于给定的两个接触点 $A,D$ 可以做出从动件的位置, 得到从动件的转动角度为 $\angle BOB'$
3. 根据相对性可得, 此角度也即从动件从 $A$ 到 $D$ 时, 凸轮的角位移
4. 现做出 $A$ 在 $DO$ 上的圆投影 $A'$, 此时 $AA'$ 在同一圆上, 需要证明 $\angle BOB'=\angle AOA'$

$$\begin{aligned} &\because A'B,AB \text{为切线} \\&\therefore\angle A'BO=\angle ABO=90^\circ \\&\because \text{根据四边形}OBCB'\text{内角和} \\&\therefore\angle A'BO+\angle ABO+\angle BOB'+\angle BCB'=360^\circ \\&\to \angle BCB'+\angle BOB'=180^\circ \\&\because \angle BCB'+\angle ACA'=180^\circ \\&\therefore \angle ACA'=\angle BOB'\\ \\&\because \begin{cases} A'O=AO \\B'O=BO \\\angle A'BO=\angle ABO=90^\circ \end{cases} \\&\therefore\Delta A'BO\cong\Delta ABO \\&\to \angle B'OA'=\angle BOA \\&\because \angle B'OA+\angle A'OA=\angle B'OA' \\&\angle B'OA+\angle BOB'=\angle BOA \\&\therefore \angle A'OA=\angle BOB' \end{aligned}$$

偏置凸轮推程运动与回程运动的不对称型

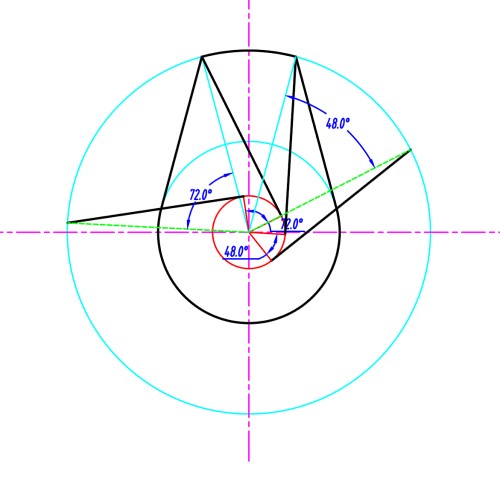
当凸轮的从动件存在偏置时, 推程运动角与回程运动角将不相同, 由于凸轮匀角速度, 因此体现为推程与回程速度不同