基础

自由度

自由度计算的问题

静定 / 超静定结构

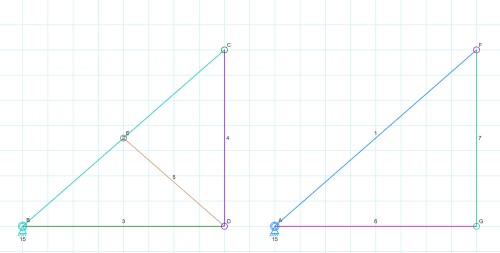
自由度计算中, 出现如图的静定 / 超静定结构, 需要将整个结构视为一个整体

复合铰链

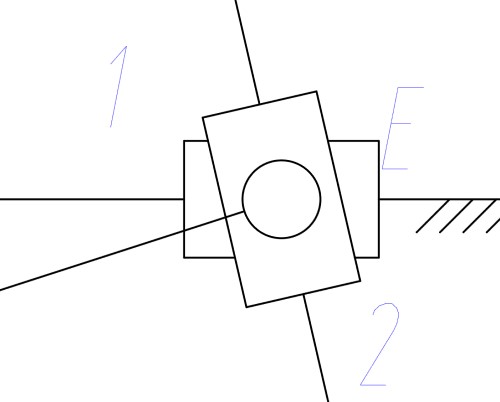
当一个铰链上同时固连了 $n(n>2)$ 个物体 (固定铰链, 滑块, 杆) 时, 则相当于有 $n-1$ 个移动副

局部自由度

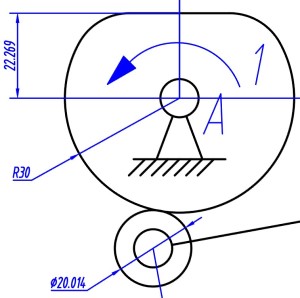
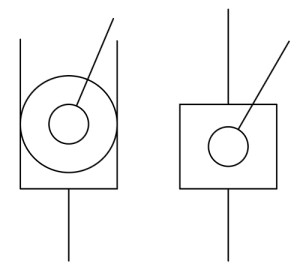
• 对于凸轮滚子与滚子滑块, 滚子的转动自由度并不重要, 可以忽略不计, 称为局部自由度
• 对于凸轮副可将滚子视为从动件的一部分
• 对于滚子滑块, 可直接视为一个滑块

轨迹重复的虚约束

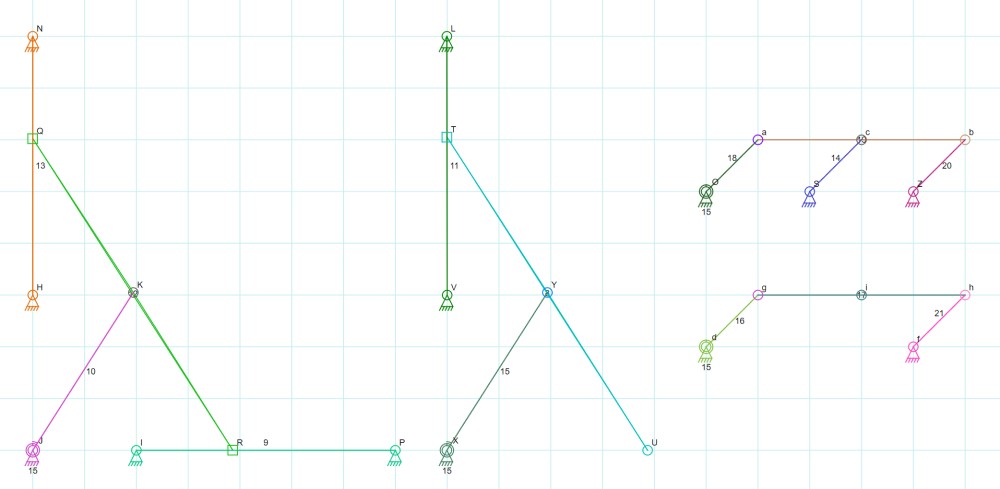
• 条件: 刚体上的约束后的轨迹与没有约束时的轨迹相同
• 去除: 去除轨迹重复的约束以及与之相连的构建
• 注意: 当出现 中点(左侧) 或 平行且相等(右侧) 的条件时注意

导路重合的虚约束

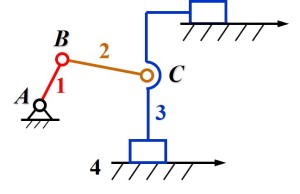
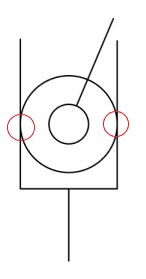
• 条件: 刚体上多个约束中, 存在两个约束, 对刚体约束的移动方向的平行
• 去除: 去除其中重复的约束
• 注意: 一个刚体上同时受到多个移动副约束 / 高副约束时注意

对称结构的虚约束

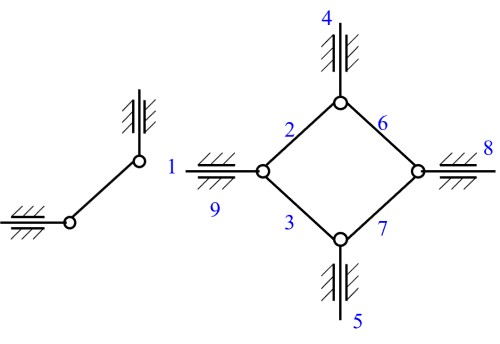
• 条件: 出现对称结构
• 去除: 去除所有对称部分, 直到不存在对称结构
• 注意: 如图结构或行星齿轮结构

平行结构的虚约束

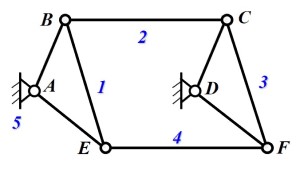
• 条件: 出现平行四边形结构
• 去除: 将平行的一侧的杆与有关约束去除, 将剩余连接合并到剩余杆上 (可能产生复合铰链等)
• 注意: 出现平行四边形结构时注意, 多层的平行结构可能还有去除中间杆

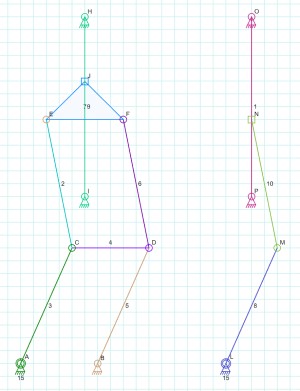
自由度计算过程

1. 标注出 结构, 局部自由度, 复合铰链, 虚约束
2. 使用 数字 标注出所有构建 (包括机架)
3. 使用 字母 标注出所有运动副
4. $DoF=3N-2P_L-P_H-3$