---

圆柱齿轮

渐开线

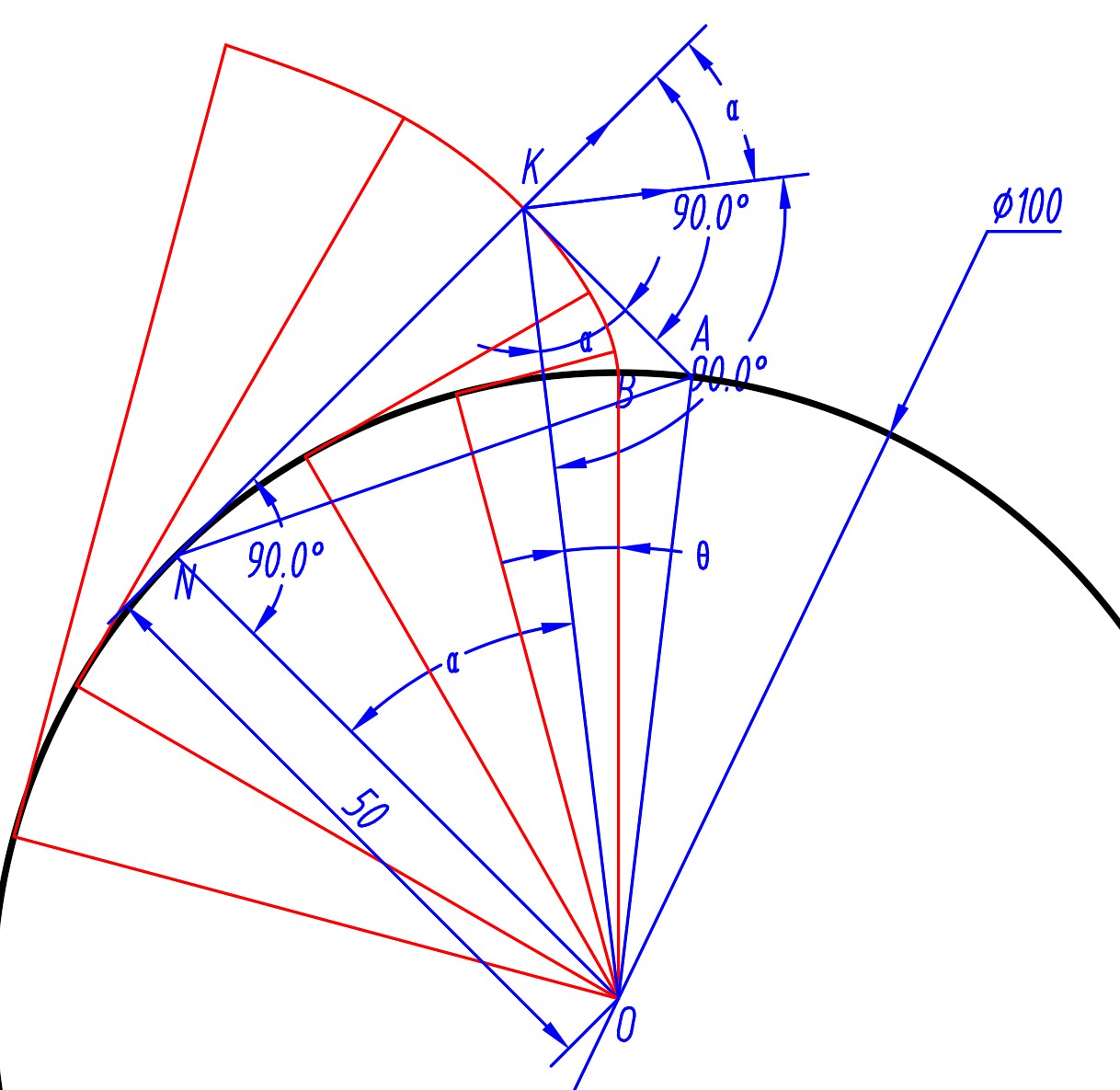
1. 设一直线与一圆, 直线与基圆做相切纯滚动时, 直线的任意一点的轨迹为渐开线
2. 基圆的半径需要确定, 但直线长度无要求
3. 定义基圆半径 $r_b=ON$

渐开线性质

渐开线法线与基圆切线重合性质

证明

假设圆静止, 直线相对圆运动, 在相切点 $N$ 处做纯滚动, $v=0$ 为速度瞬心, 直线端点 $K$ 相对 $N$ 转动, 易得速度方向, 即轨迹的切线方向垂直于直线

结论

渐开线上任意一点的法线为基圆的切线 (接触点为切点), 基圆的切线必定为渐开线的法线 (体现了直线上的点绕切点转动)

渐开线法线长性质

直线 $NK$ 与圆运动开始时在 $N$ 点, 运动到 $K$ 与 $B$ 重合, 可得圆相对于直线运动了 $NK$, 直线相对于圆运动了 $\overgroup{NB}$, 因此有

$$NK=\overgroup{NB}$$

渐开线压力角性质

1. 如图, $K$ 点的渐开线法线方向为压力 $F$ 的方向; $KO$ 垂线方向为 $K$ 点速度 $v_k$ 的方向, 夹角 $\alpha$ 即渐开线齿轮于 $K$ 的压力角
2. 根据角度关系易得 $\angle AKO=\alpha$
3. 根据法线与切线的性质做 $K$ 点切线 $AK$ 平行于直径 $NO$, 因此有 $\angle KON=\alpha$, 因此对于渐开线上一点 $K$, 法线切点 $N$ 与圆心 $O$ 构成的角大小等于压力角
4. 因此有 $\cos\alpha=\frac{KO}{NO}=\frac{r_k}{r_b}$

同一基圆上的渐开线

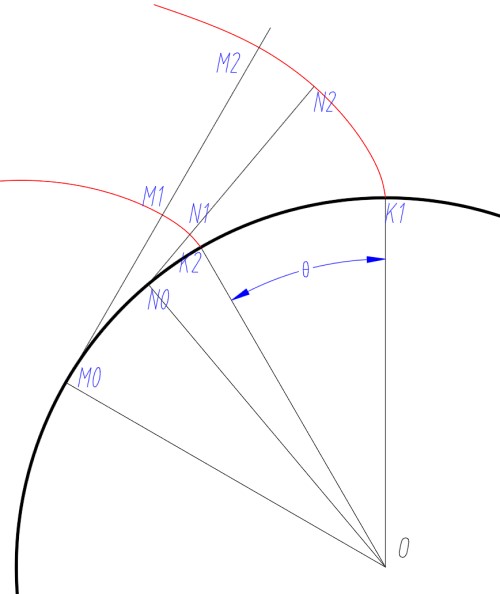
• 如图, 在同一基圆上的有两条渐开线, 其与基圆交点与圆心的夹角为 $\theta$, 两渐开线相当于绕圆心 $O$ 转过了 $\theta$
• 根据渐开线法线与基圆切线重合性质, 基圆上任意一点的切线同时为两渐开线的法线, 设切线交两条渐开线于 $N_1,N_2$
• 根据渐开线法线长性质, 有

$$N_1N_2=N_2N_0-N_1N_0=\overgroup{K_1K_2}=r\theta$$

• 因此同一基圆上的渐开线对于任意基圆切线方向的距离 (不进入基圆内) 始终为常数, 大小为基圆半径与转角之积

渐开线的其他性质

1. 对于直线 (齿条) $r_b\to\infty$ , 其渐开线也为一条直线, 对于渐开线上任意点的压力角相同
2. 由于渐开线来自刚体相对运动的轨迹, 因此基圆内无渐开线

渐开线极坐标参数方程

根据渐开线的压力角性质, 可将压力角作为参数, 与渐开线于基圆交点所在直径的夹角 $\theta$ 作为极角, 原点到渐开线上的线段作为极径 $r_k$, 有关系式

$$\tan\alpha=\frac{\overgroup{NB}}{r_b}=\frac{r_b(\alpha+\theta)}{r_b}=\alpha+\theta$$

$$r_k=r_b\cos\alpha$$

定义函数

$$inv(\alpha)=\tan\alpha-\alpha$$

可以得到渐开线的极坐标参数方程

$$\begin{cases} \theta&=inv(\alpha)\\ r_k&=\frac{r_b}{\cos\alpha} \end{cases}$$

基本参数

齿轮的基本参数

通过以下参数就能够唯一确定一个标准齿轮, 标准齿轮的其他尺寸均由此导出

名称	符号	含义
齿数	$z$	齿轮的齿数
模数	$m$	分度圆满足 $\pi d=pz$, 为使 $d$ 与 $z$ 为整数便于测量, 规定模数 $m=p/\pi$
分度圆压力角	$\alpha=20^{\circ}$	即标准齿轮相互啮合时的压力角

为了得到其他尺寸, 还需要以下标准化参数

1. 齿顶高系数 $h_a^*=1$
2. 顶隙系数 $c^*=0.25$

齿轮上的圆

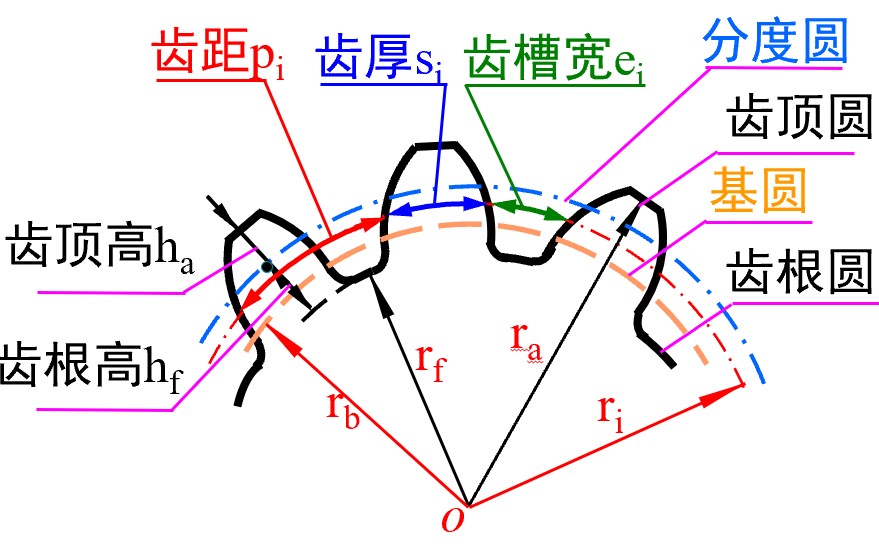
名称	符号	位置
齿顶圆	$a$	齿顶轮廓所在圆
齿根圆	$f$	齿根轮廓所在圆, 与渐开线齿形存在过渡
基圆	$b$	齿形渐开线的基圆, 通常在齿根圆外, 因此齿根圆上无压力角
分度圆	$i$ (可省略)	人为规定的具有标准模数与压力角的圆, 对于标准齿轮啮合时, 与节圆重合
节圆	$'$	当齿轮啮合时, 相对速度瞬心 $P$ 所在的圆, 仅存在于啮合齿轮中, 通过上标 $'$, 来表示 (注意与其他不同)

圆上的基本尺寸

• 对于一个齿轮, 其上任意圆均具有以下基本尺寸
• 对于不同半径的圆, 基本尺寸不同
• 默认情况下 (无下标), 均值分度圆上的尺寸

名称	符号	含义	表达式(分度圆)
齿距	$p$	相邻轮齿同侧在圆弧上的宽度, 满足 $p=e+s$	$p=\pi m$
齿槽宽	$e$	相邻轮齿之间在圆弧上的宽度	$e=s=p/2$
齿厚	$s$	轮齿两侧之间在圆弧上的宽度	$e=s=p/2$
压力角	$\alpha$	即此半径下齿轮接触点的压力角, 根据渐开线性质可算得	$r_k=r_b/\cos\alpha_k$

齿轮基本尺寸

名称	符号	含义	表达式(分度圆)
齿顶高	$h_a$	齿顶圆到分度圆的距离	$h_a=h_a^*m$
顶隙	$c$	啮合齿轮齿顶圆到另一齿轮齿根圆的距离, 防止干涉	$c=c^*m$
齿根高	$h_f$	齿根圆到分度圆的距离	$h_f=(h_a^*+c^*)m$
齿高	$h$	齿顶圆到齿根圆的距离	$h=h_f+h_a$
分度圆直径	$d$	$d=mz$
齿顶圆直径	$d_a$	$d_a=d+2h_a$
齿根圆直径	$d_f$	$d_f=d+2h_f$
基圆直径	$d_b$	使分度圆满足其压力角条件	$d_b=d\cos\alpha$
标准中心距	$a$	两个标准齿轮无侧隙传动 ($p_1=p_2$) 时的中心距	$a=r_1+r_2=\frac{m}{2}(z_1+z_2)$

传动特性

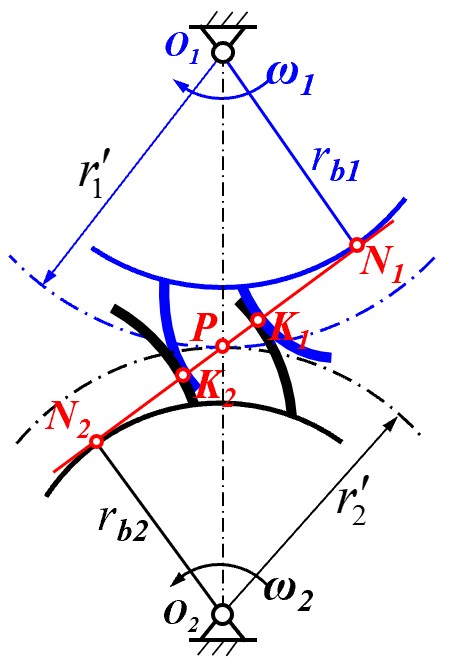
除有说明, 均针对渐开线齿轮讨论

一般齿轮传动特性

1. 此特性对任何形状的齿轮均成立
2. 根据三心定律, 两齿轮对于机架的瞬心为各自圆心, 两齿轮之间的瞬心在其圆心连线上
3. 对于啮合点 $K$ 认为是分别相对于齿轮圆心转动, 因此对于两个齿轮上的 $v_k$ 分别垂直于 $O_1K$ 与 $O_2K$
4. 点 $K$ 作为两个物体的接触点, 两个物体上 $v_k$ 沿接触点公法线方向的分量必定相同, 因此可得齿轮的瞬心于其接触点的公法线上, 因此公法线与中心线交点即齿轮瞬心 $P$
5. 对于瞬心 $P$, 两齿轮上在瞬心位置的速度大小方向均相同, 有 $v_p=O_1P\omega_1=O_2P\omega_2$
6. 定义传动比 $i_{12}=\frac{\omega_1}{\omega_2}=\frac{O_2P}{O_1P}$, 因此, 只要 $P$ 点位置不变就可以保证传动比不变

渐开线齿轮的恒定传动比

1. 渐开线齿轮的啮合点即两齿轮渐开线的切点 $K$
2. 根据渐开线性质, $K$ 分别位于两齿轮基圆的一条切线上, 并且两条切线共线, 为 $K$ 点处的公法线
3. 对于两个位置固定的基圆与固定方向的齿面上的任意啮合点, 公法线唯一, 并且即两个基圆的一条公切线 $N_1N_2$
4. 因此渐开线齿轮满足传动比不变的条件, 具有稳定的传动比, 并且啮合点只会出现在公切线上, 因此也称为啮合线

中心距可变性

1. 当中心距变化, 两个基圆的公切线随之变化, 因此 $P$ 点的位置并不固定
2. 任意中心距始终有 $\Delta O_2N_2P\sim \Delta O_1N_1P$
3. 因此传动比 $i_{12}=\frac{\omega_1}{\omega_2}=\frac{O_2P}{O_1P}=\frac{r_2}{r_1}$, 对于任何中心距, 当基圆不变, 传动比不变

啮合角可变性

1. 定义啮合齿轮的节圆的公切线 (即中心线过 $P$ 的垂线) 与接触点的公法线的夹角为啮合角 $\alpha'$, 啮合角即节线上的压力角
2. 根据角度关系可得 $\angle N_1PO_1=\angle N_2PO_2=\alpha'$, 即渐开线在瞬心 $P$ 点的压力角 (不是分度圆)
3. 可得啮合角满足 $\cos\alpha'=\frac{r_{b1}}{O_1P}=\frac{r_{b2}}{O_2P}$, 由于 $O_1P$ 与 $O_2P$ 随中心距变化, 因此啮合角也仅随中心距变化
4. 对于标准齿轮的啮合, 分度圆与压力角重合, 数值上 $\alpha'=\alpha$, 并且对于两齿轮啮合角相同

正确啮合条件

1. 当前一对轮齿于 $K_1$ 点接触时, 后一对轮齿的渐开线必须在啮合线上的另一点接触 (不是实际接触), 否则将产生干涉或传动比不连续
2. 定义法节 $p_n$ 为两个轮齿同侧两个齿面, 在啮合线上的交点的距离 (不同于齿距是在圆弧上的宽度), 根据渐开线性质满足 $p_n=p_b$ (注意不同齿面的渐开线原点不同)
3. 为了满足正确啮合条件, 可得两齿轮的法节满足 $p_{n1}=\pi m_1\cos\alpha_1=p_{n2}=\pi m_2\cos\alpha_2$
4. 因此正确啮合的条件为两齿轮的 模数与 (分度圆) 压力角相同

连续传动条件

1. 连续传动以正确啮合为前提, 但正确啮合了也不一定能连续传动
2. 当两个齿轮啮合时, 始终存在接触点, 保证动力始终能通过接触点传输, 则称齿轮能够连续传动
3. 根据上一结论可得正确啮合的齿轮理论接触点在啮合线上始终相距 $p_n$
4. 假设接触点在啮合线上移动, 必然从一个齿轮的齿顶圆与接触侧渐开线的交点开始, 从另一点分离, 因此两点构成的线段为接触点允许存在的范围, 称为实际啮合线 $B_1B_2$
5. 因此要满足连续传动的条件需要有 $\varepsilon_\alpha=\frac{B_1B_2}{p_n}>1$ 其中, 定义重合度 $\varepsilon_\alpha$
6. 假设接触点在啮合线上均匀分布, 线段 $B_1B_2$ 沿啮合线移动, 即可视为齿轮传动时接触点的状况, 可由此计算某一时刻接触点的数量
7. 为了更好的传动效果, 重合度越高越好, 并且有需用重合度 $[\varepsilon_\alpha]$, 设计齿轮后, 需要校核重合度是否大于许用值
8. 补充: 由于渐开线不能进入基圆内, 因此啮合点必定在基圆外, 因此定义啮合线在两个基圆的切点 $N_1N_2$ 为理论啮合线

重合度的计算

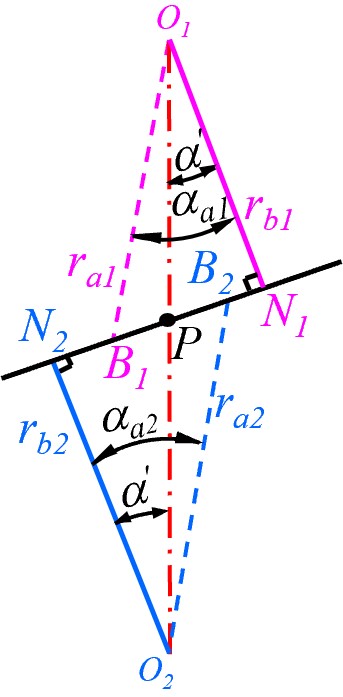
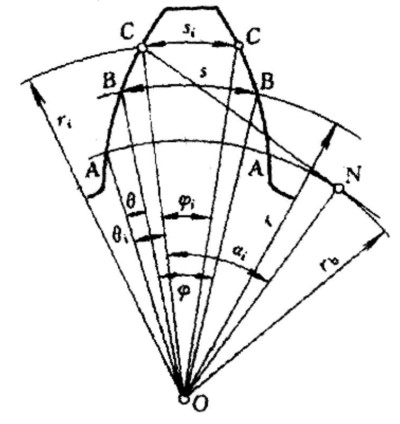
1. 根据压力角定义, 可得渐开线上交于齿顶圆的点 $B$ 与渐开线法线与基圆切点 $N$ 以及圆心构成的角 $\angle NOB=\alpha_a$; $P$ 点的压力角即啮合角 $\alpha'$,
2. 根据图形可得到以下几何关系

   1. $$r_{bi}=r_i\cos\alpha_i=\frac{mz_i}{2}\cos\alpha_i$$

   2. $$B_iN_i=r_{bi}\tan\alpha_{ai}$$

   3. $$N_1N_2=r_{b1}\tan\alpha'+r_{b2}\tan\alpha'$$

   4. $$B_1B_2=B_1N+B_2N-N_1N_2$$

   5. $$p_n=2\pi r_{bi}/z=\pi m\cos\alpha_i$$

   6. $$\varepsilon_\alpha=\frac{B_1B_2}{p_n}=\frac{z_1(\tan\alpha_{a1}-\tan\alpha_{a}')+z_2(\tan\alpha_{a2}-\tan\alpha_{a}')}{2\pi}$$

   7. $$\cos\alpha_{ai}=r_{bi}/r_{ai}$$

齿轮齿条

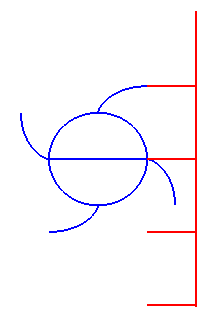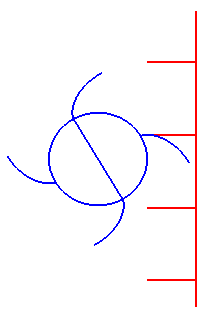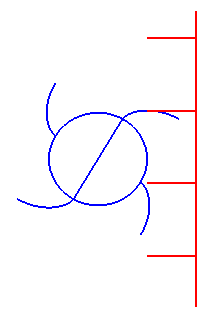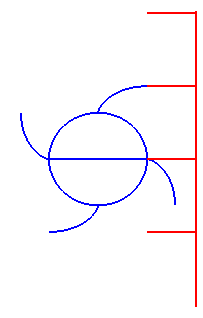
齿条的几何特点

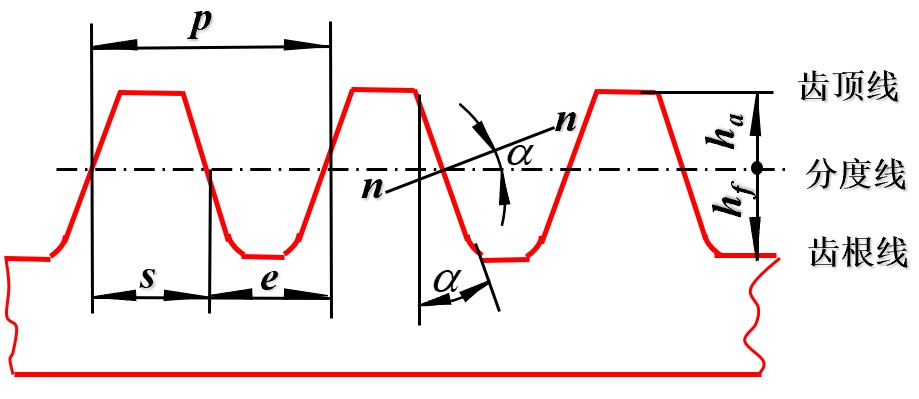
1. 渐开线齿廓变为直线, 此时渐开线上各点的压力角相同 (速度方向水平, 力垂直于齿廓)
2. 分度线垂线与齿形角的夹角称为齿形角, 等于压力角 $\alpha$
3. 由于齿形为直线, 因此齿条齿廓上各点的压力角相同 (注意圆柱齿轮上各点的压力角不同)
4. 齿条齿形上各点的齿距相同 (因此模数也相同), 但只有分度线满足 $e=s$
5. 齿条上没有五圆, 但相应的有五线, 其中分度线为齿条上 $e=s$ 的参考线, 齿根线与齿顶线根据 $h_a$ 与 $h_f$ 得到

齿轮齿条的啮合特点

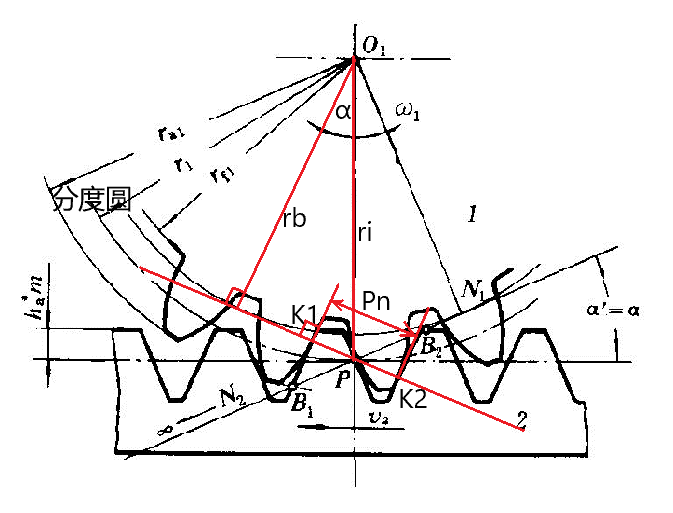
几何分析

1. 由于齿条的齿形为直线, 因此齿条上每个接触点的公法线与水平线的夹角均为 $\alpha$, 并且相互平行
2. 齿轮与齿条对于一个在 齿轮圆心与齿条运动方向直线上的 瞬心 $P$ 做纯滚动
3. 因此接触点的公法线必定过此接触点 (接触点只能向垂直于公切线的方向运动), 且所有接触点的公法线重合, 即一条过 $P$ 点的, 与水平线的夹角为 $\alpha$ 的线, 即啮合线, 并且啮合角等于压力角 $\alpha$
4. 根据渐开线的性质, 此啮合线也将切于基圆
5. 根据正确啮合的条件可得与, 如图所示, 此时齿条的法节 $p_n=p\cos\alpha$ 也要与齿轮相同, 因此啮合齿轮齿条的模数与压力角也将相同
6. 根据如图的几何关系可得, 公法线垂直于齿条的齿形, 因此瞬心 $P$ 所在的圆满足 $r_i=r_P=r_b/\cos\alpha$, 因此瞬心 $P$ 位于分度圆上 (注意齿轮齿条压力角相同)

参数定义

1. 由几何关系可得, 齿轮齿条啮合时, 瞬心一定在分度圆上, 因此节圆一定是分度圆, 节线一定是过瞬心的分度圆的切线, 啮合齿轮齿条上, 分度圆与节线的相对几何位置始终不变
2. 由速度瞬心可得有传动关系 $v_2/\omega=r_1=\frac{1}{2}mz_1$
3. 定义齿轮圆心到分度线的垂直距离为齿轮齿条的中心距
4. 齿条的分度线与节线无关, 中心距无法改变分度圆大小, 因此齿轮齿条的传动比不受中心距影响

变位齿轮

变位齿轮的形成

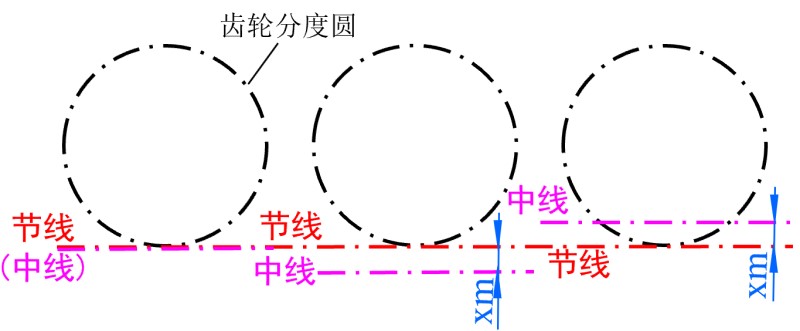
1. 在范成法加工齿轮中, 当节线与分度线重合时, 得到的齿轮为标准齿轮, 即分度圆上满足 $e=s$
2. 当分度线与节线不重合时, 将产生变位齿轮, 变位齿轮分度圆上的 $e\neq s$, 高度关系 $h_a,h_f$ 与标准齿轮不同, 但模数与压力角不变
3. 定义变位系数 $\chi$, 分度线与节线的距离为 $\Delta=m\chi$, 以远离齿轮中心的方向为正

变位齿轮的特点

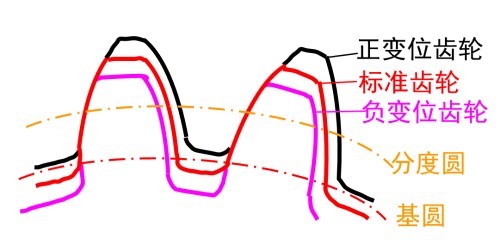
1. 正变位中, 齿条齿顶线靠近分度圆, 因此能增大齿厚
2. 负变位中, 齿条齿根线靠近分度圆, 因此将减小齿厚

齿轮根切

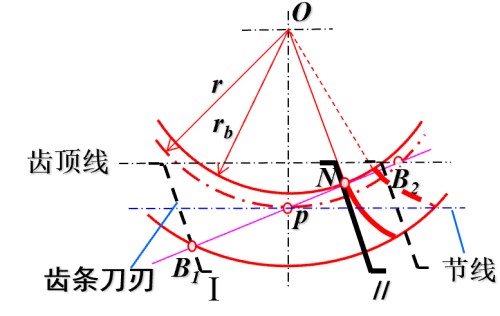
1. 范成法加工中, 齿条沿一个方向移动, 其齿廓与啮合线的交点即齿轮齿廓线 (接触点)
2. 当交点超过齿顶线后, 齿轮齿条分离, 因此啮合线与齿顶线的交点决定了渐开线齿廓的终点 (实际啮合线)
3. 由于渐开线不能在基圆内生成, 因此渐开线齿廓的终点不能进入基圆内, 即基圆切点 (理论啮合线), 否则将导致根切, 使齿轮强度降低
4. 可得发生根切的条件是 齿条齿顶线高于 啮合线 上与基圆切点所在直线 (注意齿条刀只沿啮合线方向切割齿轮), 即啮合线上 $PB_2>PN$
5. 其中 $B_2$ 点不是齿顶圆在啮合线的交点, 而是齿条齿顶线在啮合线的交点, 因此有 (注意齿轮齿条啮合时, 啮合角始终有 $\alpha'=\alpha$, 不受变位影响) $PB_2=\frac{(h_a^*-\chi)m}{\sin\alpha}$
6. 通过三角形 $\Delta OPN$ 几何关系有 $PN=r\sin\alpha$
7. 由此得到直圆柱齿轮不发生根切的条件为 (与模数无关) $PN\ge PB_2\to z\ge\frac{2(h_a^*-\chi)}{\sin^2\alpha}$
8. 通过增大齿数可以避免根切, 对于标准齿轮, 不产生根切的最少齿数是 $z=17$
9. 也可以使用正变位避免根切, 正变位下, 分度线与齿顶线向下移动, 防止齿顶线超过理论啮合线
10. 标准齿轮不产生根切的最小变位系数为 $\chi_{min}=\frac{17-z}{17}$

分度圆齿厚

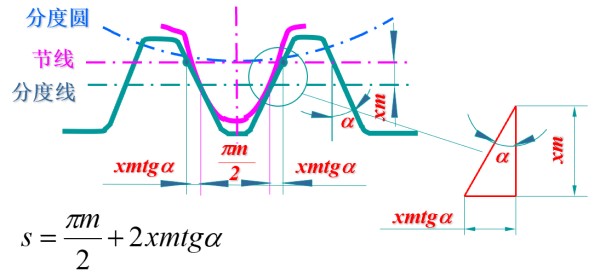
1. 齿轮齿条本质为分度圆在节线上的纯滚动, 因此节线上的齿厚 $s$ 等于分度圆上的齿槽宽 $e$
2. 因此变位的本质为改变齿廓两侧渐开线的距离
3. 根据变位系数计算得到节线上的齿槽宽增大 $2\chi m\tan\alpha$ (以分度线向下移动为变为系数 $\chi$ 的正值)
4. 因此变位齿轮分度圆上有 $s=\frac{\pi m}{2}+2\chi m\tan\alpha$, 相应的得到齿厚满足 $e=p-s=\frac{\pi m}{2}-2\chi m\tan\alpha$

齿轮中心距

1. 对于一般齿轮, 中心距为节圆的半径和, 因此有实际中心距 $a'=r_1'+r_2'$
2. 对于标准齿轮正确啮合时, 标准中心距满足 $a=\frac{1}{2}m(z_1+z_2)$
3. 根据啮合角可变性可得, 在实际节圆上其与啮合角满足关系 $r'_i=\frac{mz_i}{2}\frac{\cos\alpha}{\cos\alpha'}$
4. 因此当啮合角大小已知时, 实际中心距的关系满足 $a'=a\frac{\cos\alpha}{\cos\alpha'}$

无侧隙啮合条件

由上可知, 中心距没有限制条件, 此时规定 (公称) 中心距为齿轮在无侧隙啮合下的中心距.
无侧隙啮合的基本条件为节圆上 $s_1'=e_2'\;e_1'=s_2'$, 即两齿轮节圆上, 一齿轮的齿槽宽等于另一齿轮的齿厚.
因此正确啮合时, 两齿轮在节圆上的齿距 $p'=r_i'/z_i$ 相同, 无侧隙啮合条件也可写为 $p'=s_1'+s_2'$.
通过渐开线参数方程以分度圆齿厚为基准, 可以推导出任意圆齿厚满足

$$\begin{split}s_k&=r_k(\psi-2\Delta\theta)\\&=r_k\frac{s}{r}-2r_k(inv\alpha_k-inv\alpha)\end{split}$$

公式中

• 抓住齿厚为圆弧长度的本质, 将齿厚弧度分解为渐开圆齿厚弧度与基准相差弧度两部分
• $\psi$ 为分度圆上齿厚的弧度
• $\Delta\theta$ 为目标圆与分度圆在渐开线交点的参数角 $\theta=inv\alpha$
• 注意左侧与右侧均有渐开线齿廓, 因此有 $2\Delta\theta$

代入无侧隙啮合条件, 得到无侧隙啮合下, 变位齿轮满足 (注意, 对于变为齿轮齿条, $\alpha'=\alpha$)

$$inv\alpha'=inv\alpha+2\frac{\chi_1+\chi_2}{z_1+z_2}\tan\alpha$$

由此解出变位齿轮啮合角, 带入中心距公式, 得到变位齿轮的公称中心距. 定义中心距变动系数

$$y=\frac{a'-a}{m}=\frac{1}{2}(z_1+z_2)(\frac{\cos\alpha}{\cos\alpha'}-1)$$

则中心距为 $a'=a+ym=a\frac{\cos\alpha}{\cos\alpha'}$.

齿根圆计算

1. 范成法中, 齿条齿顶线决定了渐开线的终点, 由此也决定了齿根圆的位置
2. 当齿条远离齿轮中心 $\chi m$, 齿根圆也就增大了相应的大小
3. 因此齿根高满足 $h_f=m(h_a^*+c^*-\chi)$, 由此推出齿根圆半径满足 $d_f=mz-2h_f=mz-2m(h_a^*+c^*-\chi)$

齿顶圆计算

范成法中, 齿顶圆的大小可通过调节坯料实现.
规定变位齿轮的齿顶圆为无侧隙啮合中, 满足顶隙条件 $c=mc^*$ 的齿顶圆直径为公称齿顶圆直径, 因此齿顶圆需要考虑中心距改变带来的影响.
此条件即 $a'-(r_{f2}+r_{a1})=mc^*$, 因此变位齿轮的齿顶圆大小必须考虑两个啮合齿轮.
两齿轮相互之间的齿顶圆与齿根圆之间满足相距一个 $c^*m$ 的特点, 可得 $r_{a1}=a'-r_{f2}-mc^*=m(\frac{1}{2}z_1+y+h_a^*-\chi_2)$.
定义齿高变动系数

$$\sigma=\chi_1+\chi_2-y$$

得到齿高 (注意 $\sigma$ 为一个与啮合两轮有关的系数)

$$h_a=m(\chi+h_a^*-\sigma)$$

已知目标中心距下的变位齿轮的计算

通过

$$a'=a\frac{\cos\alpha}{\cos\alpha'}$$

计算得到啮合角大小.
通过

$$inv\alpha'=inv\alpha+2\frac{\chi_1+\chi_2}{z_1+z_2}\tan\alpha$$

计算得到变位传动参数 $\chi_1+\chi_2$.
根据额外约束条件确定 $\chi_1,\chi_2$, 通常小齿轮采用正变位, 大齿轮不变为或负变位.
齿根圆 $d_{f1},d_{f2}$ 仅随变位中齿条分度线的移动而移动, 因此可直接计算得到 (注意改变了 $2\chi_i m$, 移动方向与变位方向相同)

$$d_{fi}=mz_i-2(h^*_a+c^*)m+2\chi_i m$$

由于两齿轮相互之间的齿顶圆与齿根圆之间满足相距一个 $c^*m$ 的特点, 因此得到齿根圆直径后可根据中心距推出齿顶圆

$$\frac{d_{a1}}{2}=a'-\frac{d_{f2}}{2}-c^*m$$

变位齿轮的传动

标准传动

当啮合的两齿轮均为标准齿轮时, 传动为标准传动, 此时节圆与分度圆重合, 中心距即标准中心距

等移距变为传动

1. 当满足 $\chi_1+\chi_2=0$ 时, 两齿轮为变为齿轮, 但实际中心距等于标准中心距
2. 通常小齿轮正变位, 大齿轮负变位, 可以实现 $z<17$

正传动

1. 当满足 $\chi_1+\chi_2>0$ 时, 实际中心距大于标准中心距
2. 当目标中心距与标准中心距不同时, 可以配凑中心距
3. 正变位下齿厚增大, 可以增加齿轮强度

负传动

1. 当满足 $\chi_1+\chi_2<0$ 时, 实际中心距小于标准中心距
2. 负变位下齿厚减小, 且易发生根切, 一般不采用

变位齿轮的设计

变位校核

1. 正变位
   • 正变位中, 齿根圆靠外 (范成齿顶线远离圆心), 因此实际啮合线较短, 需要校核重合度 $\varepsilon$
   • 正变位中, 取用渐开线顶部, 渐开线快速闭合, 因此齿顶容易变尖 ($s_a$ 过小), 需要校核齿顶圆齿厚 $s_a$
2. 负变位
   • 负变位中, 范成法齿顶线靠近圆心, 需要校核是否发生根切

模数选择

1. 模数越大, 齿轮越厚大, 齿轮抗弯强度越大
2. 模数越小, 重合度越大, 传动越平稳, 在满足抗弯强度的条件下, 模数越小越好

齿数选择

1. 减小机构尺寸, 需要选择较小的齿数
2. 增大齿轮传动的平稳性, 需要选择较多齿数
3. 齿数最好选择不可互约的质数, 以获得更好的传动效果

斜齿轮

• 将直圆柱齿轮的每一个截面相对于上一个截面旋转一个角度 $d\theta$ 得到斜齿轮

基本参数

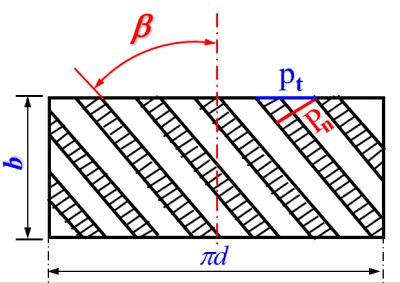
法面与端面

• 研究斜圆柱齿轮时通常会沿某一半径的圆柱面剖切, 然后将圆柱面展开
• 展开圆柱面后, 齿形截线成平行斜线, 将垂直于齿形截线的平面称为法面, 采用下标 $n$, 定义法面上的参数为标准值
• 将展开面的圆周长所在平面称为端面, 采用下标 $t$, 端面上的参数为对齿轮直接测量得到的值
• 定义螺旋角为法面与端面的夹角为螺旋角 $\beta$, 也等于齿形截线与竖直方向的夹角
• 由于不同半径下圆的周长不同, 端面上齿数相同, 因此不同圆柱展开面中, 螺旋角不同, 以分度螺旋面上的螺旋角为标准值

模数

• 根据三角关系, 端面与法面齿距满足关系

$$p_n=p_t\cos\beta$$

• 不同面下的模数通过齿距计算公式定义, 因此有 $m_n z=m_t z\cos\beta$, 得到两个面上的模数满足

$$m_n=m_t\cos\beta$$

半径计算

• 齿顶高计算对于两个面的模数分别成立, 因此两个面的齿顶高系数不相同 (法面为标准值)

$$h_a=h_{an}^*m_n=h_{at}^*m_t$$

• 齿根高计算同理, 因此顶隙系数同样不同

$$h_f=(h_{an}^*+c_a^*)m_n=(h_{at}^*+c_t^*)m_t$$

• 对于半径等参数, 只能是端面上的值 (法面上无意义) , 因此计算分度圆半径时, 应使用 $m_t$, 或将给出的标准值 $m_n$ 转为 $m_t$

$$r=\frac{m_t z}{2}=\frac{m_n z}{2\cos\beta}$$

• 由于标准中心距为两圆分度圆的半径和, 因此计算时也需要用端面参数 $a=\frac{m_n}{2\cos\beta}(z_1+z_2)$
• 对于齿根高与齿顶高则只需要加上 / 减去相应的高度即可

几何特点

压力角

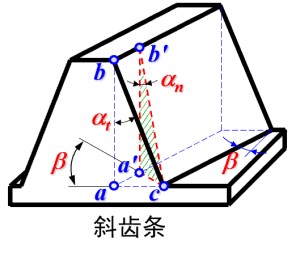
• 啮合角等于压力角的特点在斜齿条上依然成立 (沿法面 / 端面截取得到的外形仍为齿条的外形), 即竖直线与齿形线的夹角等于压力角 $\alpha$
• 由于法面 / 端面截取得到的外形不同, 因此对于端面与法面上的压力角不同
• 如图, 对于端面上, 压力角满足 $\tan\alpha_t=\frac{ac}{ab}$
• 在法面的齿条截面里, $\tan\alpha_n=\frac{a'c}{a'b'}$, 其中 $a'b'=ab,\;a'c=ac\cos\beta$, 因此两个面上的压力角满足

$$\tan\alpha_n=\frac{ac\cdot\cos\beta}{ab}=\tan\alpha_t\cos\beta$$

• 此结论对于一般斜齿轮成立

啮合条件

• 平行轴斜齿轮啮合的基本条件与直圆柱条件相同, 要求两斜齿轮模数与压力角相同
• 除了基本条件, 当两齿轮轴平行时, 在啮合处的齿形应相同, 即一齿底部的螺旋方向与另一齿顶部的螺旋方向相同, 即啮合两轮螺旋角满足条件

$$\beta_1=-\beta_2$$

重合度

1. 在端面上观察, 斜齿轮重合度计算与直圆柱齿轮一致, 称为端面重合度 $\varepsilon_{\alpha}$, 并且需要使用端面法节 $p_{nt}$ 作为同侧两齿接触点的距离
2. 在轴向上观察, 啮合点形成的曲线与轴线不平行, 斜齿上的啮合点在轴向投影是一条长为 $c$ 的线段 (直圆柱齿轮为一个点)
3. 在基圆柱上展开齿轮, 可得前后端面的齿廓渐开线与基圆的弧长为 $b\tan\beta_b$ ($b$ 为齿宽), 将前后端面的渐开线投影到同一平面上, 根据啮合性质 (啮合点沿两基圆公法线) 与渐开线性质 可得, 部分啮合长度等于此弧长, 有 $c=b\tan\beta_b$
4. 当啮合线段恰好进入实际啮合线 $B_1B_2$ 时, 两齿轮开始有接触点, 当啮合线段完全离开 $B_1B_2$ 时, 两齿轮完全没有接触点, 由此可得, 啮合线段相当于使啮合线增长了, 定义增长部分的重合度为 $\varepsilon_{\beta}=\frac{b\tan\beta_b}{p_{nt}}$

轴向重合度公式推导

• $$p_{nt}=p_t\cos\alpha_t=\frac{\pi m_n\cos\alpha_t}{\cos\beta}$$

• 根据基圆与分度圆圆柱展开面的宽 (齿宽) 与齿数相同, 长满足 $2\pi r$ 的关系可得, 设分度圆上 $\tan\beta=\frac{x}{b}$, 底边长 $x=2\pi r$

$$\tan\beta_b=\frac{x\frac{r_b}{r}}{b}=\tan\beta\cos\alpha_t$$

• 联立两式可得到轴向重合度公式为

$$\varepsilon_\beta=\frac{b\sin\beta}{\pi m_n}$$

当量齿数

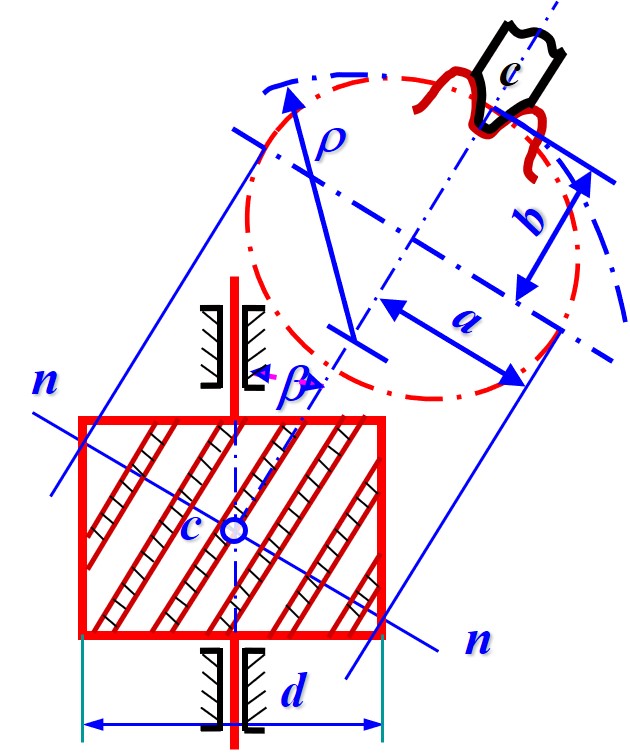
1. 使用仿形法铣齿时与斜齿啮合 (范成法) 时, 主要受力方向平行于法面, 为了研究这些问题, 首先需要研究以法面为截面上的齿形
2. 由于法面实际为螺旋面 (圆柱展开面上的法面为直线) , 无法直接研究, 通过寻找一个齿形与法面齿形相同的直圆柱齿轮来等效替代
3. 此等效齿轮的齿距已知, 即法向齿距 $p_n=\pi m_n=\pi m_t\cos\beta$, 压力角也已知, 即法向压力角 $\tan\alpha_n=\tan\alpha_t\cos\beta$, 还需要计算这个等效齿轮的齿数或分度圆半径
4. 可得分度圆半径即法面与圆柱面相交得到的螺旋线的曲率
   1. 取斜齿轮分度圆柱面上的点 $c$, 法面螺旋面在 $c$ 处的位面为一斜截面, 截面从分度圆柱面上截出一椭圆
   2. 可得, $c$ 点位于椭圆短半轴端点上, 螺旋线在 $c$ 点的曲率等于 $c$ 点在此椭圆上的曲率
   3. 椭圆长轴即正面投影 $a=r/\cos\beta$, 短轴即侧面投影 $b=r$
   4. 由此可得 $c$ 点处的曲率半径为 $\rho=a^2/b=r/\cos^2\beta$, 且对于螺旋线上任意一点, 曲率半径均相同, 因此 $\rho$ 即此等效齿轮的分度圆半径
5. 根据此分度圆半径, 可以计算出此等效齿轮的齿数, 定义此齿数为当量齿数

$$z_v=\frac{2\rho}{m_n}=\frac{2r}{m_t\cos^3\beta}=\frac{z}{\cos^3\beta}$$

斜齿轮根切

1. 计算斜齿轮根切问题时, 通过推广直圆柱齿轮的根切公式计算
2. 对于斜齿轮, 根切发生在端面上, 因此需要将端面参数带入直圆柱齿轮公式
3. 由此得到标准斜齿轮不发生根切的条件为

$$z\ge\frac{2h_{at}^*}{\sin^2\alpha_t}=2h_{an}^*\cos\beta(1+\frac{\cos^2\beta}{\tan^2\alpha_n})$$

标准圆锥齿轮

球面渐开面

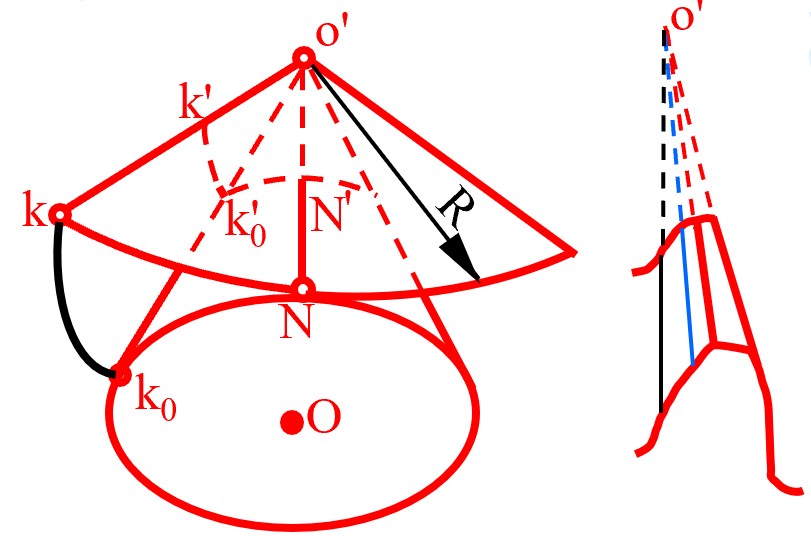
1. 一半径为 $R$ 的扇形在基圆锥上相切纯滚动, 扇形与圆锥始终有一条接触线
2. 扇形的端点在空间中的轨迹为球面渐开线, 由于始终满足 $KO'$ 长度不变, 因此可得曲线在球面上
3. 扇形的边 $O'K$ 扫过的曲面可视为 $(0,R)$ 的一系列扇形产生的球面渐开线之和
4. 球面渐开线的性质与渐开线性质类似, 球面渐开线的法面为基圆锥的切面, 因此锥齿轮采用球面渐开面作为齿廓

背锥齿廓

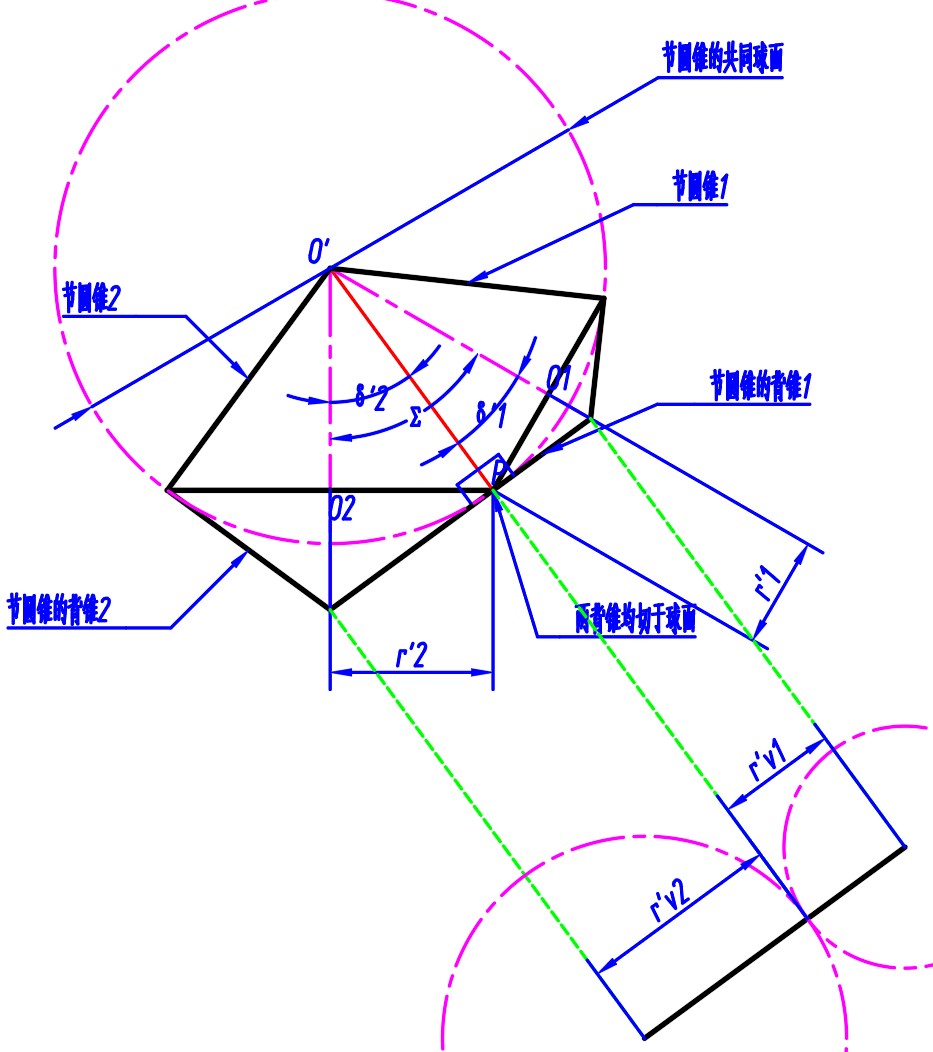
1. 两锥齿轮的圆锥的顶点为其回转轴的交点, 并且节圆锥相切于一条母线
2. 过此相切直线与圆锥大端直径做截面, 称为轴剖面, 得到如图
3. 由上两条性质可得, 两节圆锥包含于一个球面内, 母线相同
4. 过两节圆锥大端分别做圆锥切于此球面, 称为背锥, 在截面上体现为背锥母线垂直于相应的圆锥母线
5. 将球面渐开线投影到背锥上, 然后将背锥展开近似得到两个啮合的扇形渐开线齿形, 由此得到锥齿轮大端的近似齿廓, 并且可得背锥上的齿距在展开后不变

基本几何特性

• 对于锥齿轮, 存在五个圆锥, 将圆锥大端半径作为圆半径, 齿轮的模数等其他参数默认采用大端参数
• 定义圆锥轴线与母线的夹角为锥顶角 $\delta$
• 定义两啮合锥齿轮的轴线交角为 $\Sigma$ (上标 $'$ 表示节圆参数)
• 将背锥展开得到的近似齿轮的半径称为当量半径, 节圆当量半径即背锥母线, 满足

$$r_{vi}'=\frac{r'_i}{\cos\delta'_i}$$

• 对于标准锥齿轮, 分度圆与节圆重合, 因此节圆参数与分度圆参数相同, 有 $r=r',r_v=r_v',\delta=\delta'$
• 由于齿轮从大端展开, 因此展开后的齿轮模数不变, 可得当量齿数与实际齿数满足

$$z_{vi}=\frac{2r_{vi}}{m}=\frac{z_i}{\cos\delta_i}$$

基本尺寸

• 对于圆锥上不同位置, 齿数相同, 模数不同, 为了方便测量, 均采用大端参数, 因此锥齿轮的模数也为大端模数
• 啮合条件除了模数与压力角相同外, 锥齿轮还要求

$$\Sigma=\delta'_1+\delta'_2$$

• 锥齿轮啮合时, 节圆锥做纯滚动, 因此有 (注意两啮合圆锥共切于同一条母线 $OP=R$ )

$$i_{12}=\frac{\omega_1}{\omega_2}=\frac{r_2'}{r_1'}=\frac{z_2}{z_1}=\frac{OP\sin\delta_2'}{OP\sin\delta_1'}=\frac{\sin\delta_2'}{\sin\delta_1'}$$

此公式说明, 啮合锥齿轮的锥顶角 $\delta$ 与锥齿轮的齿数有关

• 一般情况下, $\Sigma=90^\circ$, 在此条件下满足 (可通过此公式计算啮合锥齿轮的锥顶角)

$$i_{12}=\frac{\sin\delta_2'}{\cos\delta_2'}=\tan\delta_2'=\frac{z_2}{z_1}$$

• 定义节圆锥的共同母线长为节锥距 $R$, 当 $\Sigma=90^\circ$ 时, 可得四边形 $OO_1PO_2$ 为矩形, 因此对于标准圆锥齿轮满足 (此时节圆参数与分度圆参数相同)

$$R=\sqrt{r_1^2+r_2^2}=\frac{m}{2}\sqrt{z_1^2+z_2^2}$$

顶锥角与根锥角

• 圆锥齿轮通常为圆台状, 定义圆台上端称为小端, 仍采用背锥齿廓
• 注意背锥由分度圆锥决定, 对于不同的圆锥, 背锥相同, 并且采用了背锥齿廓, 因此齿顶高等参数要在背锥母线上取 (或等效齿廓)
• 对于大端上的齿顶圆与齿根圆满足 (注意 $\cos\delta$ 为将背锥上的高度投影到圆锥底面)

$$r_a=r+h_a\cos\delta=r+h^*_am\cos\delta$$

$$r_f=r-h_f\cos\delta=r-(h^*_f+c^*)m\cos\delta$$

• 对于圆锥齿轮啮合, 定义顶隙大小为其中一个齿轮的齿顶圆锥与另一齿轮的齿根圆锥在轴剖面上的投影, 两圆锥母线间距离
• 注意对于标准圆锥齿轮, $c^*=0.2$, 与圆锥齿轮不同

收缩顶隙传动

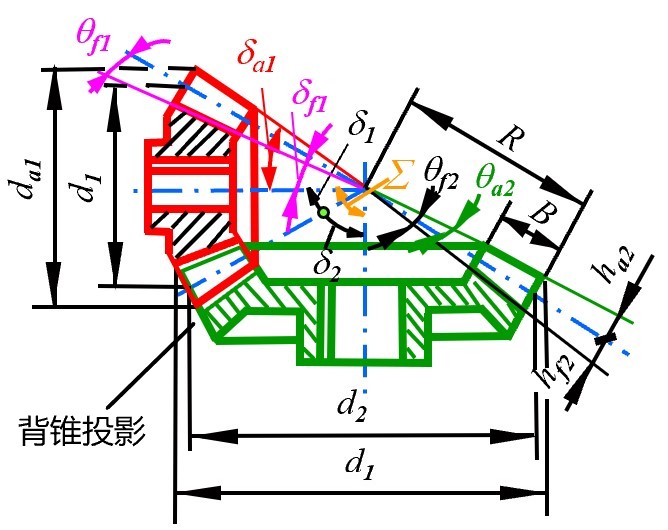
• 当啮合两圆锥的齿顶圆锥, 分度圆锥, 节圆锥, 齿根圆锥, 基圆锥的锥顶均重合与一点时, 定义为收缩顶隙传动
• 此时两齿轮的顶隙线最终也将交于一点, 因此顶隙从大端到小端不断缩小, 将影响齿轮强度
• 齿根圆与齿顶圆的锥顶角满足 (注意啮合两齿的齿顶高, 分度圆锥顶角等参数不同)

$$\delta_{ai}=\delta_i+\theta_{ai},\,\tan\theta_{ai}=h_{ai}/R$$

$$\delta_{fi}=\delta_i+\theta_{fi},\,\tan\theta_{fi}=h_{fi}/R$$

等顶隙传动

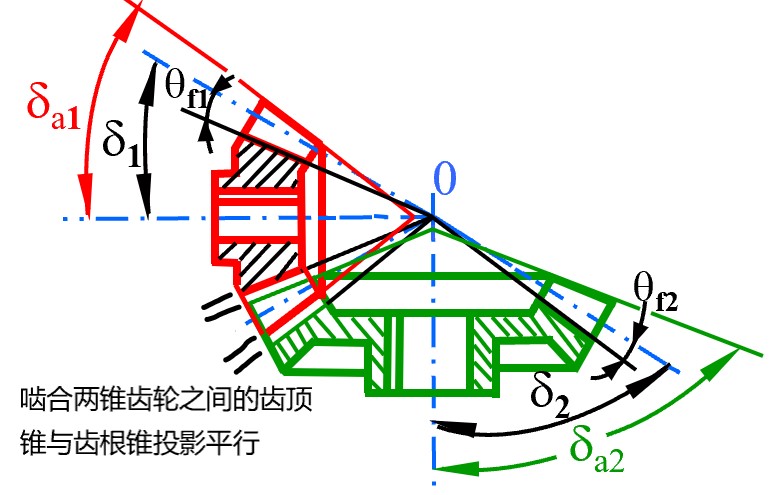
• 当两啮合圆锥齿轮的顶隙不变时, 定义为等顶隙传动
• 由于顶隙不变, 因此两啮合圆锥之间的齿顶锥与齿根锥投影母线平行
• 通过改变两齿轮的齿顶圆锥来达到这一效果, 齿顶圆锥的锥度减小, 使小端上的齿顶圆减小, 防止小端齿廓变尖并且降低齿高增加了齿轮的强度
• 齿根圆不变, 依然满足

$$\delta_{fi}=\delta_i+\theta_{fi},\,\tan\theta_{fi}=h_{fi}/R$$

• 根据母线平行这一条件, 可以得到齿顶圆锥顶角仅与另一啮合齿轮的齿根圆锥有关

$$\delta_{a1}=\Sigma-\delta_{f1}=\delta_1-\theta_{f2}$$