齿轮系

齿轮传动特点

齿轮系机构简图

1. 通过三段线段表示俯视齿轮简图
2. 通过点画线表示正视齿轮简图
3. 通过箭头表示轮系的转动方向, 其中箭头方向为轮系靠近观察者一侧的转动方向

外啮合齿轮传动特点

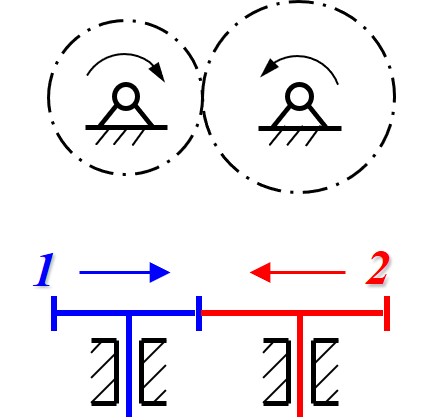
1. 外啮合的两齿轮转动方向相反, 体现为外啮合的两齿轮箭头相对或相离
2. 啮合的两齿轮轴线平行, 因此可用负传动比表示传动关系

内啮合齿轮传动特点

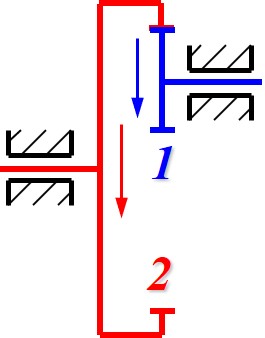
内啮合的两齿轮转动方向相同, 体现为内啮合的两齿轮箭头方向相同

锥齿轮传动特点

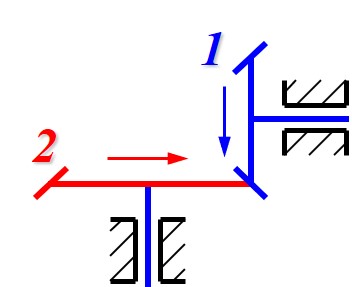
锥齿轮下啮合两齿轮转动轴线垂直, 与外啮合相同, 将齿轮箭头方向相对或相离

蜗轮蜗杆传动特点

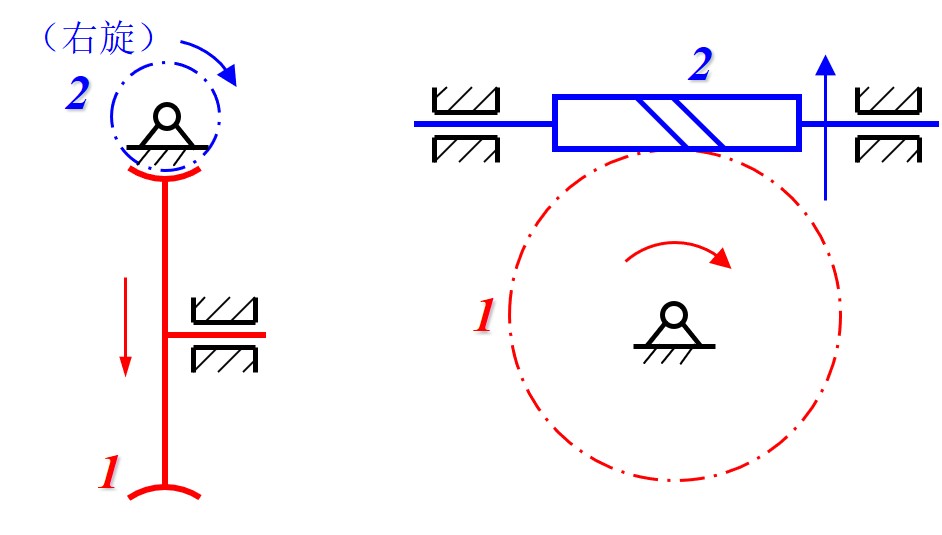
1. 注意啮合的蜗轮蜗杆旋向相同, 并且判断旋向时需要将轴线旋转至竖直方向
2. 通过将螺旋线的旋转等效为齿轮齿条的移动判断旋转方向 (蜗杆到蜗轮); 或等效齿轮齿条的移动判断对应的螺旋旋转方向 (蜗轮到蜗杆)
3. 传动时轴线垂直不平行

齿轮系中的机构编号

1. 对于一般的机构采用阿拉伯数字编号, 并且通常将主动件标 $1$
2. 对于齿轮系中的轴采用罗马数字编号 (非必要)
3. 对于行星齿轮系中的非固定轴 / 摇臂采用 $H_n$ 编号
4. 对于同一根轴上的多个传动机构, 输入机构正常编号 $n$ , 其他机构编号为 $n'$, 根据机构数量增加上标 $'$

定轴齿轮系的传动比

定轴轮系的传动比

• 对于两个啮合的齿轮, 其中 $j$ 为主动轮, $k$ 为从动轮, 传动比满足

$$i_{jk}=\frac{\omega_j}{\omega_k}=\frac{z_k}{z_j}$$

根据齿轮啮合点上两齿轮的速度相同得到 (相对速度瞬心), 其中 $z$ 为齿轮的齿数, 对于蜗杆则为头数

• 对于从主动轮 $1$ 到输出机构 $k$, 传动比满足

$$i_{1k}=\frac{\omega_1}{\omega_k}=(-1)^m\frac{\prod_{i=1}^n z_{bi}}{\prod_{i=1}^n z_{ai}}$$

• 公式中
  • 系数 $(-1)^m$ 仅用于同轴的定轴轮系, 且使用前需要规定转向的正方向, $m$ 为外啮合对数
  • $z_{ai}$ 为各个主动件的齿数, 位于分母
  • $z_{bi}$ 为各个从动件的齿数, 位于分子

传动比计算过程

1. 确认输入机构 (轴) 与输出机构 (轴)
2. 从输出机构反推到输入机构, 寻找其传动链
3. 列出此传动链上的各个齿轮, 使用如下格式表示 $z_1\to z_2(z_2')\to z_3(z_3')\to\dots z_k$
   • 使用括号表示位于同一轴上的输出机构
   • 箭头左侧 (通常为括号内) 为主动件, 右侧为从动件
4. 使用公式计算得到传动比 $i$

周转轮系的传动比

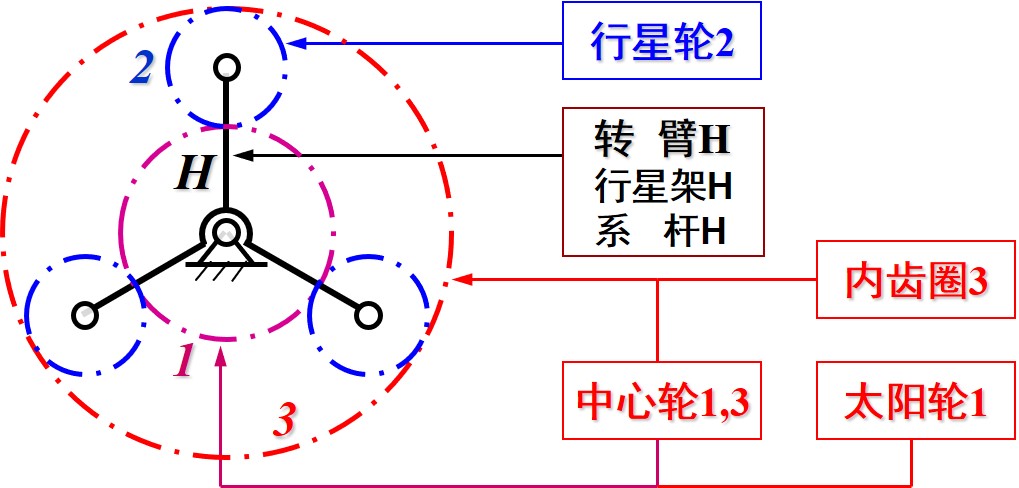
1. 在齿轮运转时, 其中至少有一个齿轮的几何轴线绕另一齿轮的几何轴线运动的齿轮系称为周转齿轮系
2. 最简单的周转轮系即行星齿轮系, 由行星轮, 中心轮, 转臂和机架组成
3. 注意对于如图的机构属于对称机构, 因此三个行星轮仅需保留一个分析即可

行星齿轮系的分析

1. 注意到行星齿轮系的自由度为 $2$, 无法像一般的但自由度的定轴轮系直接分析传动比
2. 通过固定转臂, 即仅计算相对转臂的速度 $\omega^H_i=\omega_i-\omega_H$以降低自由度以求解运动关系, 使用上标表示相对对象

周转轮系的传动比计算

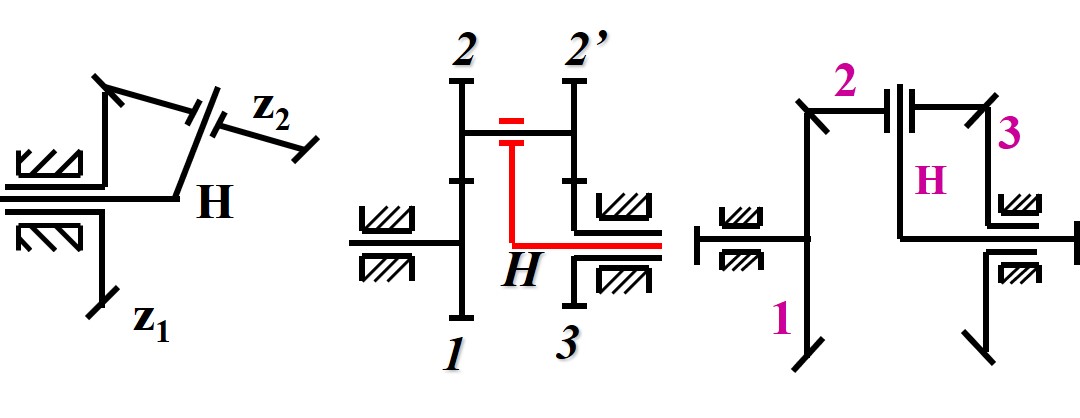
• 在转臂固定后, 转化为定轴轮系, 因此有相对传动比

$$i^H_{13}=\frac{\omega_1-\omega_H}{\omega_3-\omega_H}=-\frac{z_3}{z_1}$$

• 因此对于多个齿轮传动, 在相对转臂 $H$ 的条件下, 传动比公式依然成立

$$i^H_{1k}=\frac{\omega_1-\omega_H}{\omega_k-\omega_H}=(-1)^m\frac{\prod_{i=1}^n z_{bi}}{\prod_{i=1}^n z_{ai}}$$

• 传动比公式在相对于任意机构下的推广

$$i_{xy}^z=\frac{\omega_x-\omega_z}{\omega_y-\omega_z}$$

• 根据推广式还可得到常用变形 (用于已知部分机构转速时, 计算其他机构的转速)

$$i_{xy}^z=1-i^y_{xz},\;i_{xy}^z=\frac{1}{i^z_{yx}}$$

• 注意本节有关传动比的讨论仅在转换轮系的首末轮回转轴线平行的周转齿轮系下成立, 对于图左侧机构不成立, 对于图右侧与中间机构虽然没有内齿轮 / 旋转轴不同但依然属于行星轮系并且满足条件, 公式成立

周转轮系的分析

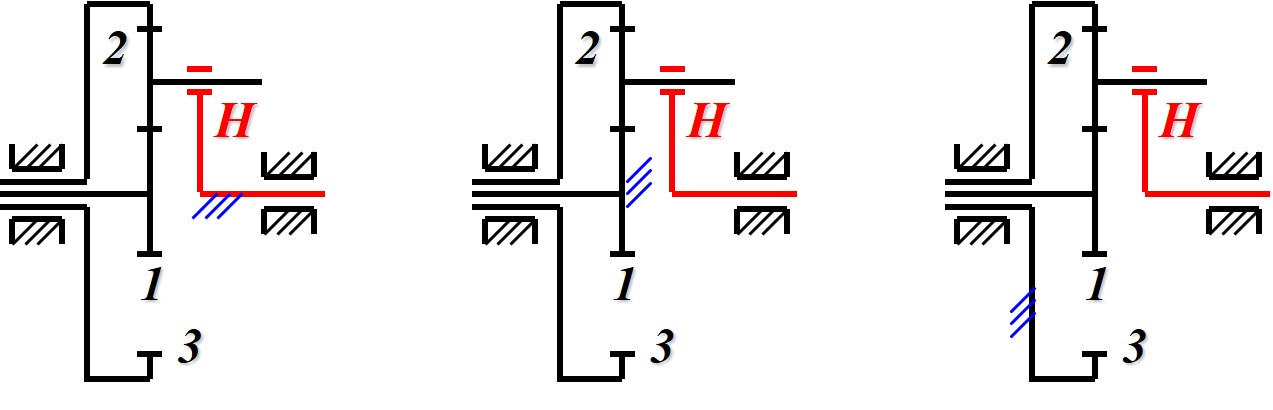
1. 由于周转轮系的自由度不为 $1$, 因此计算绝对传动比关系时需要直到至少一个机构的运动状况
2. 如果要确定机构具体的运动状况, 则需要两个条件
3. 除题干外, 注意观察运动简图中与机架固连的部分, 如图所示当机构上有机架符号时表示与机架固连, 固连机构的绝对速度 $\omega=0$
4. 注意 $i^H_{1k}$ 为相对传动比, 因此一般情况下 $i^H_{1k}\neq i_{1k}$, 仅当相对机构 $H$ 静止时等式成立
5. 分析运动状况 / 传动比时, 需要利用相对传动比公式及其推广
6. 由于公式要求首末轮回转轴线平行, 当首末轮转向相反时, 传动比为负, 且公式 $i_{xy}^z=1-i^y_{xz}$ 中也包含了负号含义, 因此在使用公式时必须先判断出首末轮转向

复合轮系的分析

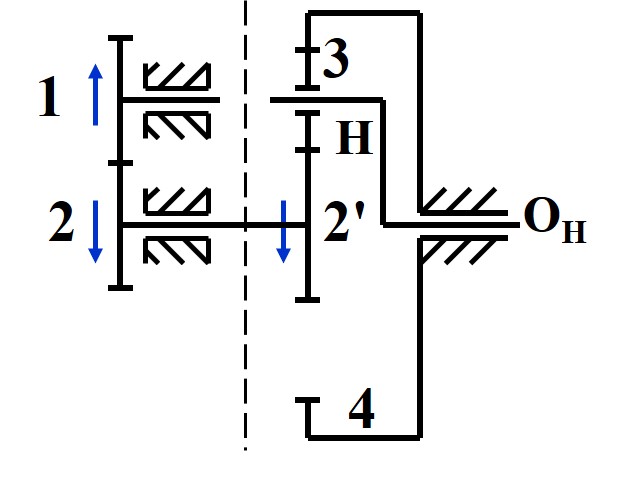
确定正方向

在进行轮系分析前, 首先要确定正方向, 并使用题目的值进行运算时也需要带入符号

确定周转轮系

1. 通常每有一个位于摇臂上的齿轮, 便意味着有一个周转轮系
2. 周转轮系仅包含摇臂上的齿轮以及与其啮合的两个齿轮
3. 通过截开周转轮系上齿轮所在轴, 将周转轮系分开
4. 剩余未被划分的轮系即定轴轮系

参数计算

1. 对于每个被划分的轮系分别计算其首末齿轮的传动比
2. 带入有关数据的到结果