傅里叶变换
参考自教程 https://www.bilibili.com/video/BV1Et411R78vopen in new window
三角函数系
对于函数集合
C=1,sinx,cosx,sin2x,cos2x,…,sinnx,cosnx
称之为三角函数系
正交性
函数集合内的任取两个不同的函数在 (−π,π) 上的卷积均为 0
将这一性质称为正交性
观察函数图像可得, 对于 sinnx,cosnx,n∈{x∈Zx=0} 均有
∫−ππsinnxdx=0,∫−ππcosnxdx=0
通过积化和差公式可得, 以下卷积的结果均为 0
sinnx∗cosmx=sinnx∗sinmx=cosnx∗cosmx=0(m=n)
同一函数卷积
当 m=n=0 时 (从 C 中选取两个相同函数), 则有
∫−ππsin2mxdx=21∫−ππ[−cos(m+n)+1]dx=π
∫−ππcos2mxdx=21∫−ππ[cos(m+n)+1]dx=π
当取 C 中的 1 时, 则有
∫−ππdx=2π
傅里叶级数
周期为 2π 的傅里叶级数
对于一个以 2π 为周期的函数 f(x)=f(x+2π)
可以将其展开为傅里叶级数
f(x)=2a0+n=1∑∞[ancosnx+bnsinnx]
根据三角函数的正交性
对于 1∗f(x), 仅 2a0 项的积分结果不为 0
∫−ππf(x)dx=21a0∫−ππdx=πa0
对于 cosnx∗f(x), 仅 ancosnx 项的积分结果不为 0
∫−ππcosnx⋅f(x)dx=an∫−ππcos2nxdx=πan
对于 sinnx∗f(x), 仅 bnsinnx 项的积分结果不为 0
∫−ππsinnx⋅f(x)dx=bn∫−ππsin2nxdx=πbn
因此傅里叶级数中的系数满足
a0anbn=π1∫−ππf(x)dx=π1∫−ππcosnx⋅f(x)dx=π1∫−ππsinnx⋅f(x)dx
周期为 2L 的傅里叶级数
对于一个以 2L 为周期的函数 f(t)=f(t+2L)
可以使用变量代换 t=πLx 将其转变为一个以 2π 为周期的函数
g(x)=f(πLx)→g(x+2π)=f(πL(x+2π))
因此将 x=Lπt 带入 g(x) 的傅里叶级数中, 即可得到 f(t) 的傅里叶级数
定义 ω0=Lπ, 三角函数换元后有
sinnx=sinnω0x,cosnx=cosnω0x
积分换元后有
∫−ππg(x)dx=Lπ∫−LLf(t)dt
因此对于周期为 2L 的傅里叶级数有
f(t)a0anbn=2a0+n=1∑∞[ancosnω0t+bnsinnω0t]=L1∫−LLf(t)dt=L1∫−LLcosnω0t⋅f(t)dt=L1∫−LLsinnω0t⋅f(t)dt
周期信号的傅里叶级数
在工程中, 信号为从 0 开始, 以 T 为周期的函数, 因此定义变换 (其中 ω0 为基频)
T=2L,ω0=T2π
易得对于周期为 2T 的函数
∫−LLf(t)dt=∫0Tf(t)dt
可以得到
f(t)a0anbn=2a0+n=1∑∞[ancosnω0t+bnsinnω0t]=T2∫0Tf(t)dt=T2∫0Tcosnω0t⋅f(t)dt=T2∫0Tsinnω0t⋅f(t)dt
例题

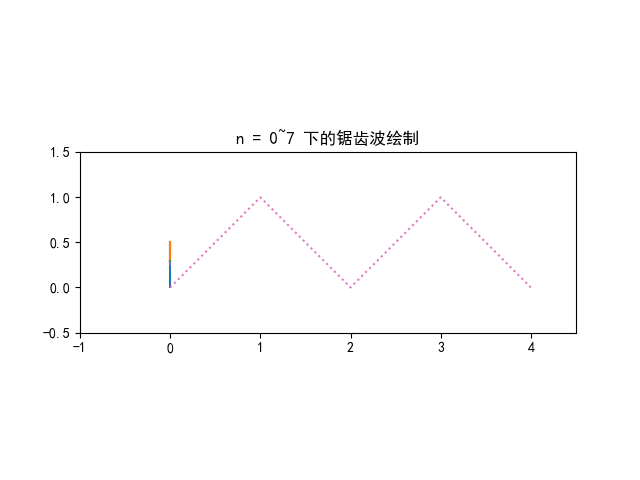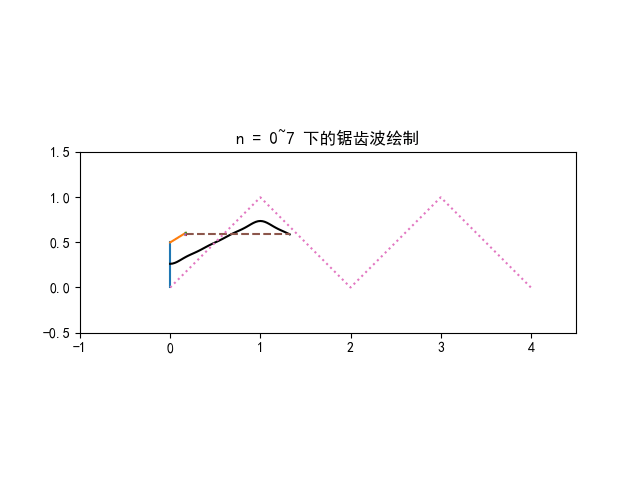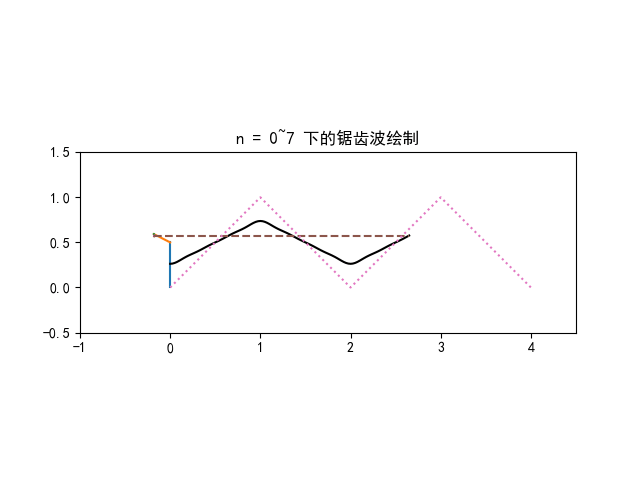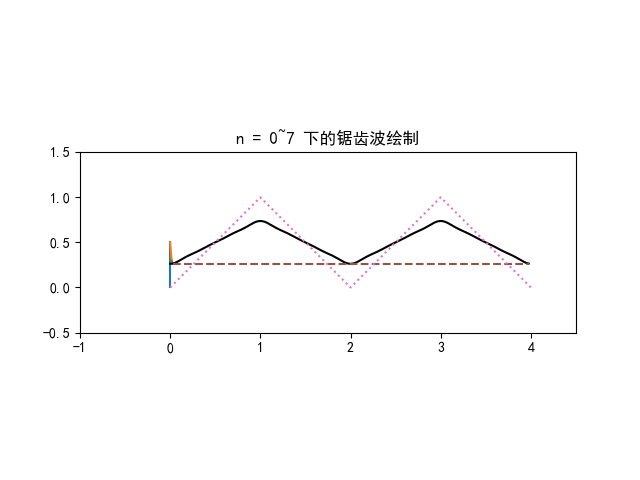
将如图所示的周期函数 f(t) 分解为傅里叶级数
如图所示, f(t) 有周期 2L=20, 取 ω0=Lπ=10π
如图, 函数在周期 L 内可以视为一个分段函数, 因此积分时分段处理
计算 a0
a0=101(∫0107dt+∫10203dt)=10
计算 an, 注意 sin(nπ)=0(n∈Z)
an=101[∫0107cos(10πnt)dt+∫10203cos(10πnt)dt]=101[7π10sin(10πnt)010+3π10sin(10πnt)1020]=0
计算 bn, 注意 cos(2nπ)=1,cos[(2n+1)π]=−1,cos(nπ)=(−1)n,n∈Z
bn=101[∫0107sin(10πnt)dt+∫10203sin(10πnt)dt]=101[−7π10cos(10πnt)010−3π10cos(10πnt)1020]=π1[7−7(−1)n+3(−1)n−3]=π4−4(−1)n
综上可得
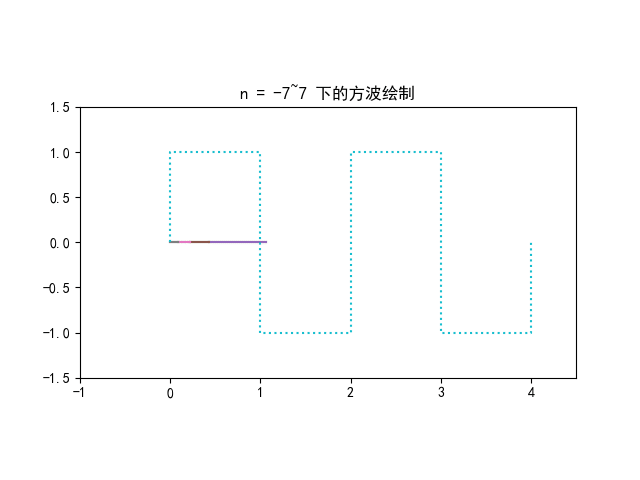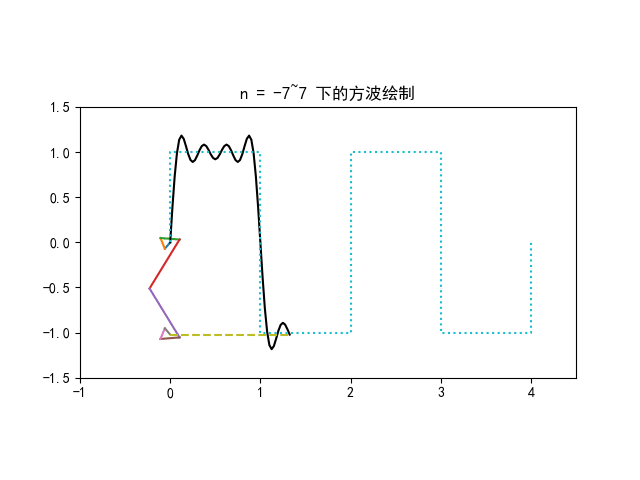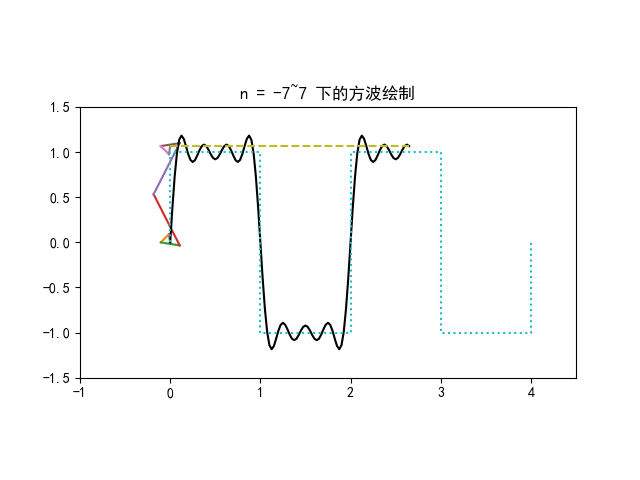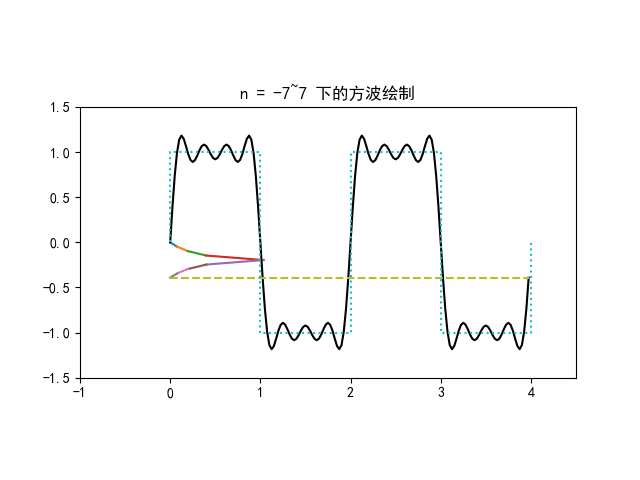
f(t)=5+n=1∑∞π4−4(−1)nsin(10πnt)
f(t) 的傅里叶级数前 4 项叠加图像
傅里叶变换推导
傅里叶级数的复数形式
三角函数的复数形式
根据欧拉公式有
eiθ=cosθ+isinθ
据此以及三角函数的奇偶性, 可将三角函数表示为复数形式
sinθ=2i1(eiθ−e−iθ)=2−i(eiθ−e−iθ)
cosθ=21(eiθ+e−iθ)
复数形式的展开
将复数形式的三角函数带入傅里叶级数
f(t)=2a0+n=1∑∞[ancos(nω0t)+bnsin(nω0t)]=2a0+n=1∑∞[2an−ibneinω0t+2an+ibne−inω0t]=2a0+n=1∑∞2an−ibneinω0t+n=−∞∑−12a−n+ib−neinω0t=−∞∑∞Cneinω0t
现推导系数 Cn
当 n=0
C0=2a0=T1∫0Tf(t)dt
当 n>0
Cn=2an−ibn=T1∫0Tf(t)⋅[cos(nω0t)−isin(nω0t)]dt=T1∫0Tf(t)⋅e−inω0tdt
当 n<0
Cn=2a−n+ib−n=T1∫0Tf(t)⋅[cos(−nω0t)+isin(−nω0t)]dt=T1∫0Tf(t)⋅e−inω0tdt
综上可得, 复数傅里叶级数的系数 Cn 对于任意 n 均有同一个表达式
Cn=T1∫0Tf(t)⋅e−inω0tdt
周期函数傅里叶级数的特点
根据傅里叶级数的复数表达, 在复平面上傅里叶级数的每一项中
- einω0t 体现了一个以 nω0 为角速度旋转的向量
- ∣Cn∣ 确定了这个向量的幅值
- Cn 确定了这个向量在 t=0 的相位角
因此周期函数的傅里叶本质上是将周期函数分解为频率为基频的整数倍 nω0 的无数个周期性旋转
即周期函数的频域以 Δω=ω0 为间隔
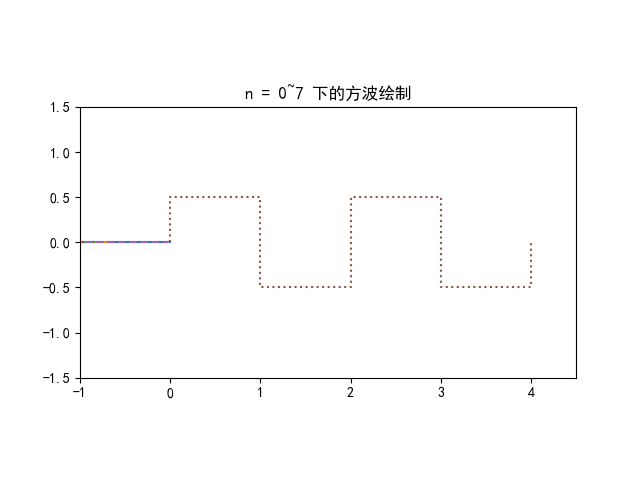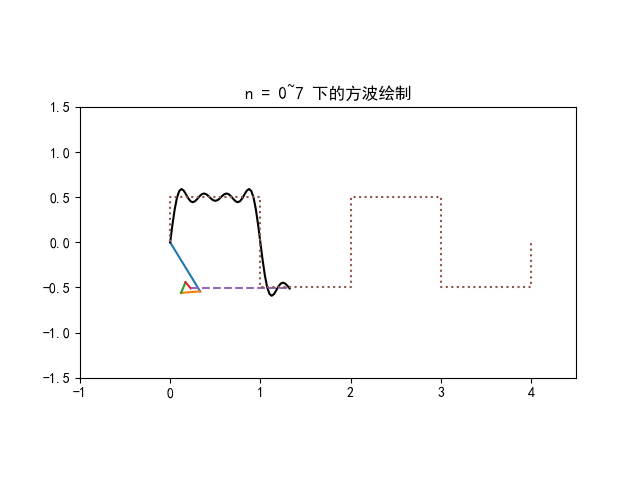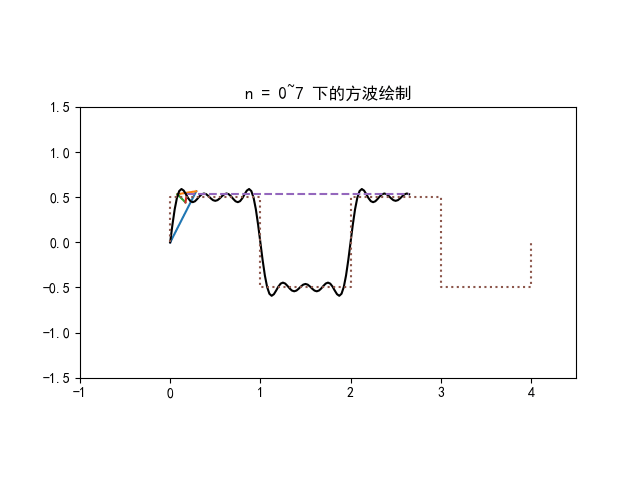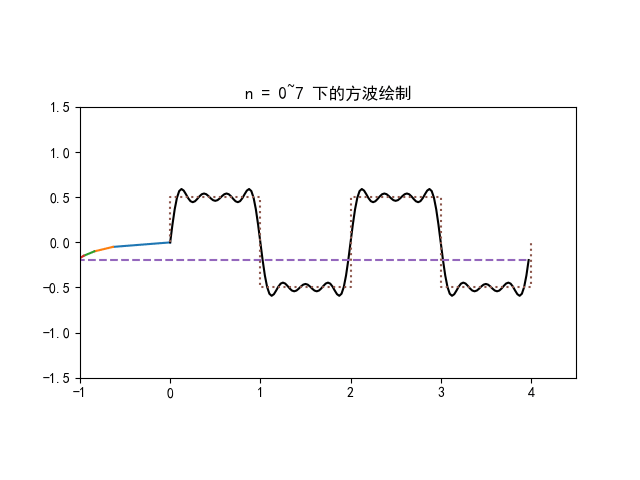
非周期函数的傅里叶变换
对于非周期函数 f(t) 其周期 T→∞, 基频 ω0→0
因此函数的频率分布之间的间隔 ω0=Δω→0, 此时函数的频域连续分布
根据以下变换
nω0→ωn=−∞∑∞s(nω0)→∫−∞∞s(ω)T1=2πΔω→2πdω
带入 f(t) 的傅里叶级数
f(t)=n=−∞∑∞Cneinω0t=T1n=−∞∑∞(∫−2T2Tf(t)e−inω0tdt)einω0t=2πdω∫−∞∞(∫−∞∞f(t)e−iωtdt)eiωt=2π1∫−∞∞(∫−∞∞f(t)e−iωtdt)eiωtdω
此时 Cn 可以被表示成一个连续的函数 F(ω), 因此有
F(ω)=F[f(t)]=∫−∞∞f(t)e−iωtdtf(t)=F−1[F(ω)]=2π1∫−∞∞F(ω)eiωtdω
其中
F(ω)=F[f(t)] 为傅里叶正变换
f(t)=F−1[F(ω)] 为傅里叶逆变换
根据推导可得, 傅里叶变换得到的 F(ω) 相当于 Cn=F(ω)dω, 因此 F(ω) 并不代表信号中频率为 ω 的成分, 而是在频率范围 ω∼dω 内的密度
因此 F(ω) 体现的是信号在 ω 的幅值密度而非幅值 (与傅里叶级数做区分)
工程应用
频率下的傅里叶变换与级数
分析时, 工程上更多采用频率 f 而非角频率
注意, 以上推导中, ω 均指角频率而非一般频率 f
根据频率与角频率之间的关系
f=2πω,f0=T1
对傅里叶变换中的积分变量进行变量代换可得
F(f)=F[f(t)]=∫−∞∞f(t)e−j2πftdtf(t)=F−1[F(f)]=∫−∞∞F(f)ej2πftdf
对傅里叶级数的复数形式做变量代换后有
Cn=T1∫−2T2Tf(t)e−j2πnf0tdtf(t)=n=−∞∑∞Cnej2πnf0t
对傅里叶级数做变量代换后有
a0=T1∫−2T2Tf(t)dtan=T2∫−2T2Tf(t)cos(2πnf0)dtbn=T2∫−2T2Tf(t)sin(2πnf0)dtf(t)=a0+n=1∑∞ancos(2πnf0)+bnsin(2πnf0)
分析频谱
定义 fn=n⋅f0 为 n 次谐波分量, 傅里叶级数中的系数 an,bn,Cn 可看作一个关于 nf0 的离散函数
a[fn]=an,b[fn]=bn,C[fn]=Cn
傅里叶级数的频谱
由于傅里叶级数中, 同一频率 fn 的两个三角函数可以通过辅助角公式合称为单个三角函数
ancos(2πnf0)+bnsin(2πnf0)=an2+bn2cos(2πnf0−φn)
因此可得到信号中频率为 fn 的分量, 并根据此分量确定信号中 fn 分量的幅值 An 与频率 φn
- 实频谱满足 a[fn]
- 虚频谱满足 b[fn]
- 幅值谱满足 A[fn]=an2+bn2
- 相位谱满足 φ[fn]=arctananbn
傅里叶级数的复数频谱
为了与傅里叶级数的频谱区分, 有关傅里叶级数的复数形式的频谱称为傅里叶级数谱或 FS 谱, 双边谱
傅里叶级数的复数频谱通常直接来自复数系数 Cn, 且存在负频率 fn<0
- FS 实频谱满足 Re[fn]=Re[Cn]
- FS 虚频谱满足 Im[fn]=Im[Cn]
- FS 幅值谱满足 A[fn]=∣Cn∣
- FS 相位谱满足 φ[fn]=Cn
傅里叶变换的频谱
根据傅里叶变换的推导可知, 傅里叶变换得到 F(f) 为频率密度函数, 但由于傅里叶变换一般以非周期信号为对象, 因此称其为非周期信号频谱或 FT 谱
注意频率密度函数 F(f) 的函数值为复数, 且是一个 (−∞,∞) 上的连续函数, 因此 FT 谱在频率上均为连续的, 且存在负频率
- FS 实频谱满足 FR(f)=Re[F(f)]
- FS 虚频谱满足 FI(f)=Im[F(f)]
- FS 幅值谱满足 ∣F(f)∣=Re[F(f)]2+Im[F(f)]2
- FS 相位谱满足 F(f)=Arctan(Re[F(f)],Im[F(f)])
频谱之间的转换
单边谱幅值与双边谱幅值 (傅里叶级数与傅里叶级数的复数形式)
由于负数频率仅代表相反的旋转方向, 频率性质与正数频率一致
因此将双边幅值谱中的正负频率对应的幅值相加即可得到单边幅值谱
周期函数的频率密度函数与频谱
由于周期信号由确定的几个频率 fn 组成, 且没有 f=fn 的频率成分
因周期信号的频率密度函数为一系列大小与其傅里叶级数有关的冲激函数, 满足
F(f)=n=−∞∑∞Cnδ(f−nf0)
- 功率谱与幅值谱
根据功率的定义, 功率谱与幅值谱之间满足
A2[fn]=(A[fn])2
- 频率与角频率的频谱
比较两种频率类型下的傅里叶系数与变换方法可得, 频率与角频率的频谱在对应的频率上相同, 仅复原方法不同
常见信号的傅里叶变换与级数
对于复杂信号的傅里叶变换可根据傅里叶变化的线性性, 拆分为几个简单信号分析, 最后再线性叠加得到信号的频谱
线性组合时, 应在原始级数系数 / 频率密度曲线的基础上进行
确定信号基频 f0 时
- 对于由三角函数组成的信号, 应提出 2π 或根据给出信息确定各个信号的频率, 其最小公约数为基频
- 对于其他信号, 则可根据信号的周期确定基频 f0=T1
余弦函数
整体信号基频为 f0, 对于其中的余弦信号
f(t)=Acos(2πkf0t)
ak=A,bn=0
C±k=2A
F(f)=2A[δ(f−kf0)+δ(f+kf0)]
正弦函数
整体信号基频为 f0, 对于其中的正弦信号
f(t)=Asin(2πkf0t)
an=0,bk=A
C±k=∓2Aj
F(f)=2Aj[−δ(f−kf0)+δ(f+kf0)]
含相位角的余弦函数
f(t)=Acos(2πkf0t+φ)
具体分析时, 可拆分为余弦函数与正弦函数之和
f(t)=Acos(φ)cos(2πkf0t)−Asin(φ)sin(2πkf0t)
或使用傅里叶变换的时移特性
f′(t)=Acos(2πkf0t)f(t)=f(t+2πkf0φ)F′(f)=2A[δ(f−kf0)+δ(f+kf0)]F(f)=2A[eφjδ(f−kf0)+e−φjδ(f+kf0)]
窗函数
对于一宽度为 T, 高度为 A 的矩形窗函数
f(t)={A,0,−2T<t<2T其余
由于为非周期信号, 因此仅有傅里叶变换
F(f)=πfAsinπfT
注意, 对于 F(f) 在 f=0 的极限 limf→0πfAsinπfT=AT



