跳至主要內容

非线性方程的数值解

大约 4 分钟

非线性方程的数值解

二分法

根据 f(a)f(b)<0f(a)f(b)<0 时, 方程的根 f(x)=0f(x)=0 在区间 (a,b)(a,b) 内
每次迭代, 二分区间 (a,b)(a,b), 保证根在区间内, 直到达到指定精度
缺陷: 无法计算如 x2=0x^2=0 的根

不动点迭代法

与线性方程组的向量序列类似, 对于方程

f(x)=0 f(x)=0

构建

x=φ(x) x=\varphi(x)

得到数列

xk+1=φ(xk) x_{k+1}=\varphi(x_k)

当 kk 足够大时, 且数列不发散, 数列收敛于方程解 x∗x^*

lim⁡k→∞xk=x∗ \lim_{k\to\infty}x_{k}=x^*

构建不动点迭代法

对于方程 f(x)=0f(x)=0

  1. φ(x)=f(x)+x \varphi(x)=f(x)+x

  2. φ(x)=x(f(x)+1) \varphi(x)=x(f(x)+1)

  3. 根据 f(x)f(x) 具体构建

不动点迭代法的收敛性

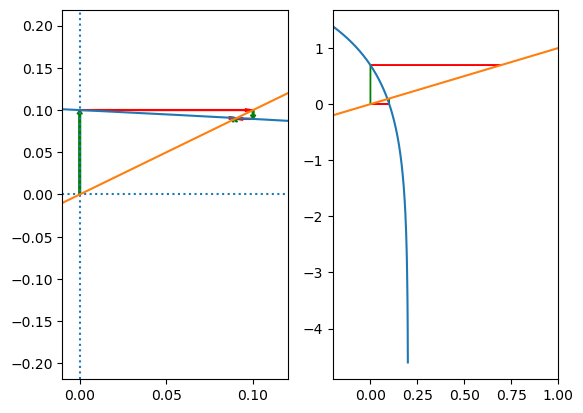
橙色直线 x=yx=y 蓝色曲线 y=φ(x)y=\varphi(x)
交点处即 x=φ(x)x=\varphi(x) 的解
对于同一个方程, 左图从 x=0x=0 处开始迭代, 向方程解收敛
右图从 x=0.1≈x∗x=0.1\approx x^* 处开始迭代, 向发散方向移动

由于 φ(x)\varphi(x) 可任意构造, 对于同一个方程, 不同的 φ(x)\varphi(x) 可能收敛也可能发散, 当 φ(x)\varphi(x) 满足以下条件时数列收敛

  1. 对于任意 x∈[a,b]x\in [a,b], 有 a≤φ(x)≤ba\le\varphi(x)\le b
  2. 对于任意 x∈[a,b]x\in [a,b], 有

∣φ(x)−φ(y)x−y∣≤L<1 |\frac{\varphi(x)-\varphi(y)}{x-y}|\le L< 1

一般带入 a,ba,b 与求导试探

不动点迭代法的误差

∣xk−x∗∣≤Lk1−L∣x1−x0∣≈L1−L∣xk−xk−1∣ |x_{k}-x^*|\le\frac{L^k}{1-L}|x_1-x_0|\approx\frac{L}{1-L}|x_{k}-x_{k-1}|

由于

L1−L≈1 \frac{L}{1-L}\approx 1

因此当要求误差

∣xk−x∗∣≤ε |x_{k}-x^*|\le\varepsilon

仅需要求

∣xk−xk−1∣≤ε |x_{k}-x_{k-1}|\le\varepsilon

迭代法的收敛性

收敛性定义

  1. 当迭代数列对于任意 x0∈Rx_0\in \R 收敛, 则称迭代数列全局收敛
  2. 当迭代数列对于任意 x0∈N(x∗,δ)x_0\in N(x^*,\delta) 收敛, 则称迭代数列局部收敛
  3. 当 ∣φ′(x∗)∣<1|\varphi'(x^*)|<1 认为数列局部收敛

收敛速度

定义迭代误差 ek=∣xk−x∗∣e_k=|x_{k}-x^*| 如果存在极限

lim⁡k→∞ek+1ekp=C \lim_{k\to\infty}\frac{e_{k+1}}{e_{k}^p}=C

则称迭代过程 x=φ(x)x=\varphi(x) 为 pp 阶收敛

根据原始定义与泰勒展开可得

ek+1=∣xk+1−x∗∣=φ(p)(ξ)p!(xk−x∗)p=φ(p)(ξ)p!ekp e_{k+1}=|x_{k+1}-x^*|=\frac{\varphi^{(p)}(\xi)}{p!}(x_k-x^*)^p=\frac{\varphi^{(p)}(\xi)}{p!}e_{k}^p

因此当 φ(x)\varphi(x) 满足

φ′(x)=⋯=φ(p−1)(x)=0φ(p)(x)≠0 \varphi'(x)=\dots=\varphi^{(p-1)}(x)=0\\\varphi^{(p)}(x)\neq 0

则称迭代过程 x=φ(x)x=\varphi(x) 为 pp 阶收敛

牛顿法

牛顿法

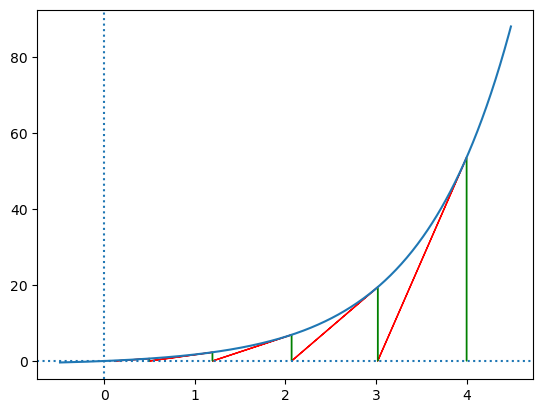
使用函数在 xkx_k 点处的切线模拟函数的值用于求解方程

f(x)≈f(xk)+f′(xk)(x−xk)=0 f(x)\approx f(x_k)+f'(x_k)(x-x_k)=0

可得到依次法构造的迭代数列为

φ(x)=x−f(x)f′(x) \varphi(x)=x-\frac{f(x)}{f'(x)}

由于 φ′(x)=0\varphi'(x)=0, φ′′(x)≠0\varphi''(x)\neq 0, 因此牛顿法为二次收敛

牛顿下山法

牛顿法中, 无法保误差稳定下降, 可能在收敛的过程中震荡, 为了保证收敛, 可引入参数与试算

试算

为了保证误差稳定下降, 在每次迭代后进行试算, 保证 (迭代越来越接近解 f(x)=0f(x)=0)

∣f(xk+1)∣<∣f(xk)∣ |f(x_{k+1})|<|f(x_{k})|

参数

引入参数 λ\lambda, 构造

φ(x)=x−λf(x)f′(x) \varphi(x)=x-\lambda\frac{f(x)}{f'(x)}

取 λ0=1\lambda_{0}=1, 每次试算不满足条件, 则取 λn+1=12λn\lambda_{n+1}=\frac{1}{2}\lambda_{n}

重根情形

当 x=x∗x=x^* 为方程的多重根, 牛顿法的收敛速度变为线性收敛

牛顿法变形

牛顿法中需要计算导数 f′(x)f'(x) 较为复杂, 可通过其他方法, 避开导数计算

简化牛顿法

取近似 f′(x)≈f′(x0)=1/Cf'(x)\approx f'(x_0)=1/C 从而有

φ(x)=x−Cf(x) \varphi(x)=x-Cf(x)

此时无法保证一定收敛, 还需要满足条件 ∣φ′(x∗)∣<1|\varphi'(x^*)|<1, 并且仅能线性收敛(p=1p=1), 但极大的简化了计算量

弦截牛顿法

使用迭代过程中计算的函数点的连线斜率近似为导数计算

f′(xk)≈f(xk)−f(xk−1)xk−xk−1 f'(x_{k})\approx \frac{f(x_k)-f(x_{k-1})}{x_k-x_{k-1}}

此方法需要给出两个初始值
此方法具有 p≈1.618p\approx 1.618 的收敛阶数, 为超线性收敛

抛物线法

类似弦截法, 但是使用二次函数近似 f(x)f(x), 而非牛顿法的一次函数
每次迭代, 使用上 33 此迭代值插值出二次多项式, 求出二次函数与坐标轴的交点, 得到下一次迭代值

应用

构造开方公式
根据开方运算, 可将其等价为方程 x2−C=0x^2-C=0 的根
使用牛顿法可得到迭代公式

xk+1=xk−xk2−C2xk=12(xk+Cxk) x_{k+1}=x_k-\frac{x_k^2-C}{2x_k}=\frac{1}{2}(x_k+\frac{C}{x_k})