跳至主要內容

插值与逼近

大约 5 分钟

插值与逼近

多项式插值

对于给定的 n+1n+1 个点, 找到 nn 次多项式满足

{a0+a1x0+⋯+anx0n=y0a0+a1x1+⋯+anx1n=y1⋮a0+a1xn+⋯+anxnn=yn \begin{cases}a_0+a_1 x_0+\dots+a_n x_0^n=y_0\\a_0+a_1 x_1+\dots+a_n x_1^n=y_1\\\vdots\\a_0+a_1 x_n+\dots+a_n x_n^n=y_n\end{cases}

即找到线性方程组的解 xx

Ax=y Ax=y

A=[1x0x02…x0n1x1x12…x1n⋮1xnxn2…xnn] A=\begin{bmatrix}1&x_0&x_0^2&\dots&x_0^n\\1&x_1&x_1^2&\dots&x_1^n\\\vdots\\1&x_n&x_n^2&\dots&x_n^n\end{bmatrix}

x=[a0a1⋮an]y=[y0y1⋮yn] x=\begin{bmatrix}a_0\\a_1\\\vdots\\a_n\end{bmatrix}y=\begin{bmatrix}y_0\\y_1\\\vdots\\y_n\end{bmatrix}

拉格朗日插值

线性函数

lk(x)=∏i≠kx−xixk−xi l_k(x)=\prod_{i\neq k}\frac{x-x_i}{x_k-x_i}

线性函数具有特点

  1. lk(xi)=0(i≠k)l_k(x_i)=0(i\neq k)
  2. lk(xk)=1l_k(x_k)=1

插值公式

利用线性函数, 可得到插值多项式

Ln(x)=∑yklk(x) L_n(x)=\sum y_k l_k(x)

牛顿插值

可根据节点的增加快速得到新的插值公式

Pn(x)=a0+a1(x−x0)+⋯+an∑i=0n(x−xi)=Pn−1(x)+an∑i=0n(x−xi) P_n(x)=a_0+a_1(x-x_0)+\dots+a_n\sum_{i=0}^{n}(x-x_i)\\=P_{n-1}(x)+a_n\sum_{i=0}^{n}(x-x_i)

均差计算

  1. 一阶均差

f[xa,xb]=f(xa)−f(xb)xa−xb f[x_a,x_b]=\frac{f(x_a)-f(x_b)}{x_a-x_b}

  1. 高阶均差

f[x0,x1,…,xn]=f[x1,…,xn]−f[x0,x1,…,xn−1]xn−x0 f[x_0,x_1,\dots,x_n]=\frac{f[x_1,\dots,x_n]-f[x_0,x_1,\dots,x_{n-1}]}{x_n-x_0}

分子为两个仅有一个点不同的均差
分母为分子中不同的点之差

均差性质

  1. 均差与节点的排列顺序无关, 即

f[x0,x1,…,xn]=f[x1,x0,…,xn]=… f[x_0,x_1,\dots,x_n]=f[x_1,x_0,\dots,x_n]=\dots

  1. 均差与导数的关系

∃ξ∈[a,b],f[x0,x1,…,xn]=f(n)(ξ)n! \exist\xi\in[a,b],f[x_0,x_1,\dots,x_n]=\frac{f^{(n)}(\xi)}{n!}

其中 xi∈[a,b]x_i\in[a,b]

均差递推

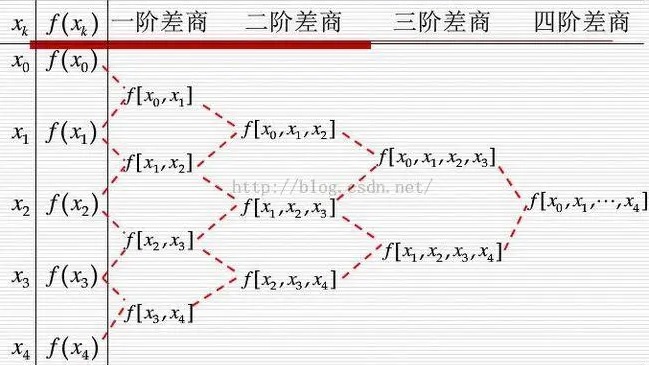
利用均差的性质可使用递推的方法得到高阶均差

插值公式

Pn(x)=f(x0)+f[x0,x1](x−x0)+⋯+f[x0,x1,…,xn]∏i=0n−1(x−xi) P_n(x)=f(x_0)+f[x_0, x_1](x-x_0)+\dots+\\f[x_0,x_1,\dots,x_n]\prod_{i=0}^{n-1}{(x-x_i)}

差分形式的牛顿插值公式

当 xtx_t 满足 xt=x0+thx_t=x_0+th 时, 可简化牛顿插值公式

差分

定义差分

Δnf(xi)−Δnf(xi+1)=Δn+1f(xi) \Delta^nf(x_i)-\Delta^nf(x_{i+1})=\Delta^{n+1}f(x_i)

差分表

利用差分的性质, 可得到递推关系

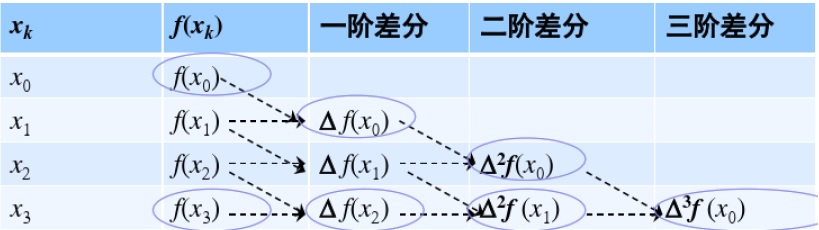
差分性质

  1. 与均差的关系

f[x0,x1,…,xn]=1n!1hnΔnf(x0) f[x_0,x_1,\dots,x_n]=\frac{1}{n!}\frac{1}{h^n}\Delta^nf(x_0)

  1. 与导数的关系

∃ξ∈[x0,x0+nh],Δnf(xi)=hnf(n)(ξ) \exist\xi\in[x_0,x_0+nh],\Delta^nf(x_i)=h^nf^{(n)}(\xi)

插值公式

Pn(x0+th)=f(x0)+Δf(x0)t+⋯+Δnf(x0)n!∏i=0n−1(t−i) P_n(x_0+th)=f(x_0)+\Delta f(x_0)t+\dots+\\\frac{\Delta^{n} f(x_0)}{n!}\prod_{i=0}^{n-1}{(t-i)}

使用此形式避免求 hnh^n, tt 可取任意实数

埃尔米特插值

实际问题还要求节点的导数满足要求, 因此可用埃米尔特插值

算术解法

类比多项式插值, 可得到其算术解法

  • 多项式

M0=[1x0x02…x0n1x1x12…x1n⋮1xkxk2…xkn] M_0=\begin{bmatrix}1&x_0&x_0^2&\dots&x_0^n\\1&x_1&x_1^2&\dots&x_1^n\\\vdots\\1&x_k&x_k^2&\dots&x_k^n\end{bmatrix}

  • 一阶导数

M1=[012x0…nx0n−1012x1…nx1n−1⋮012xn−k…nxn−kn−1] M_1=\begin{bmatrix}0&1&2x_0&\dots&nx_0^{n-1}\\0&1&2x_1&\dots&nx_1^{n-1}\\\vdots\\0&1&2x_{n-k}&\dots&nx_{n-k}^{n-1}\end{bmatrix}

  • 多项式条件与导数条件

y′=[y0′y1′⋮yn−k′]y=[y0y1⋮yk] y'=\begin{bmatrix}y'_0\\y'_1\\\vdots\\y'_{n-k}\end{bmatrix}y=\begin{bmatrix}y_0\\y_1\\\vdots\\y_k\end{bmatrix}

  • 系数向量

x=[a0a1⋮an] x=\begin{bmatrix}a_0\\a_1\\\vdots\\a_n\end{bmatrix}

  • 算术解矩阵

[M0M1]x=[yy′] \begin{bmatrix}M_0\\M_1\end{bmatrix}x=\begin{bmatrix}y\\y'\end{bmatrix}

余项表达式

  • 如果给出高阶导数条件等多个关于同一点的条件 cic_i 次, 则变为相应次数 (默认给出点条件, 因此一般情况下 ci=1c_i=1)
  • mm 为总共给出的条件数, m=∑cim=\sum c_i
  • nn 为总共的点数
  • 对于多项式表达式, 其余项表达式为

R(x)=f(x)−P(x)=1m!f(m)(ξ)∏i=0n(x−xi)ci,ξ∈(x0,xn) R(x)=f(x)-P(x)=\frac{1}{m!}f^{(m)}(\xi)\prod_{i=0}^n(x-x_i)^{c_i},\xi\in(x_0,x_n)

分段插值

龙格现象

插值多项式的次数越高, 精度不一定高
因此对于多个点, 一般不采用高次插值多项式, 而是分段第次插值

三次样条插值

使用三次多项式 Si(x)S_i(x) 对于各个点的最小区间分段插值函数 S(x)S(x)
总共需要 4n4n 个条件, 根据已知点, 可提供 n+1n+1 个条件(i=0,1,…,ni=0,1,\dots,n)

连续性条件

S(xi+)=S(xi−) S(x_i^+)=S(x_i^-)

S′(xi+)=S′(xi−) S'(x_i^+)=S'(x_i^-)

S′′(xi+)=S′′(xi−) S''(x_i^+)=S''(x_i^-)

共能提供 3n−33n-3 个条件(减去边界点)

边界条件

以上只能提供 4n−24n-2 个条件, 还差 2 个边界条件, 如果没有给出则使用自然边界条件

S′′(x0)=S′′(xn)=0 S''(x_0)=S''(x_n)=0

曲线拟合

最小二乘法概念

对于线性无关的函数族 φ0(x),φ1(x),…,φm(x)\varphi_0(x),\varphi_1(x),\dots,\varphi_m(x), 对于函数族任意线性组合 S(x)S(x), 存在函数 S∗(x)=∑i=0maiφi(x)S^*(x)=\sum_{i=0}^m a_i\varphi_i(x) 使误差平方和最小, 即满足

∣δ∣2=∑i=0nωi[S∗(xi)−yi]2=min⁡∑i=0nωi[S(xi)−yi]2 |\delta|^2=\sum_{i=0}^n\omega_i[S^*(x_i)-y_i]^2=\min\sum_{i=0}^n\omega_i[S(x_i)-y_i]^2

其中函数族内函数个数 m≤nm\le n, nn 为拟合点个数

  • 通常取 φi(x)=xi\varphi_i(x)=x^i
  • ωi\omega_i 表示点 ii 的权重, 通常取 11

最小二乘法计算

令 ∣δ∣2=I(a0,a1,…,am)|\delta|^2=I(a_0,a_1,\dots,a_m) (不是 S∗S^*), 问题变为找到使 II 最小的点, 可得到 II 满足 mm 个条件

∂I∂aj=2∑i=0nωi[S∗(xi)−yi]φj(xi)=0 \frac{\partial I}{\partial a_j}=2\sum_{i=0}^n\omega_i[S^*(x_i)-y_i]\varphi_j(x_i)=0

法方程

规定记号

  1. (φj,φk)=∑i=0nωiφj(xi)φk(xi) (\varphi_j,\varphi_k)=\sum_{i=0}^n\omega_i\varphi_j(x_i)\varphi_k(x_i)

  2. (f,φk)=∑i=0nωiyiφk(xi)=dk (f,\varphi_k)=\sum_{i=0}^n\omega_iy_i\varphi_k(x_i)=d_k

规定符号

x=[a0a1⋮am]d=[d0d1⋮dm] x=\begin{bmatrix}a_0\\a_1\\\vdots\\a_m\end{bmatrix}d=\begin{bmatrix}d_0\\d_1\\\vdots\\d_m\end{bmatrix}

G=[(φ0,φ0)(φ0,φ1)(φ0,φ2)…(φ0,φm)(φ1,φ0)(φ1,φ1)(φ1,φ2)…(φ1,φm)⋮(φm,φ0)(φm,φ1)(φm,φ2)…(φm,φm)] G=\begin{bmatrix}(\varphi_0,\varphi_0)&(\varphi_0,\varphi_1)&(\varphi_0,\varphi_2)&\dots&(\varphi_0,\varphi_m)\\(\varphi_1,\varphi_0)&(\varphi_1,\varphi_1)&(\varphi_1,\varphi_2)&\dots&(\varphi_1,\varphi_m)\\\vdots\\(\varphi_m,\varphi_0)&(\varphi_m,\varphi_1)&(\varphi_m,\varphi_2)&\dots&(\varphi_m,\varphi_m)\end{bmatrix}

可将最 S∗(x)S^*(x) 的条件表示为方程 $$Gx=d$$ 解出 xx 即可得到 S∗(x)S^*(x) 其中函数族内函数个数 m≤nm\le n, nn 为拟合点个数

哈尔条件

函数族 φ0(x),φ1(x),…,φm(x)\varphi_0(x),\varphi_1(x),\dots,\varphi_m(x) 的任意线性组合 S(x)S(x) 在定义域内, 最多只能有 nn 个零点, 才可保证矩阵 GG 可得到唯一解(非奇异)

多项式的次数

多项式的次数取决于系数不为 00 的项中的最高次数
eg. 1+x2=01+x^2=0 为二次多项式, 包含的函数族为 1,x,x21,x,x^2

转化为多项式

通常采用多项式作为拟合函数, 拟合超越函数时, 可使用多项式变形

U(x)=f[S(x)]=a′g(x)+b′y′=f(y) U(x)=f[S(x)]=a'g(x)+b'\\y'=f(y)

求出 y′y' 与 g(x)g(x) 的关系, 得到 S(x)S(x)

指数拟合

S(x)=aebx S(x)=ae^{bx}

令

U(x)=lnS(x)=lna+bx U(x)=lnS(x)=lna+bx

幂函数拟合

S(x)=axb S(x)=ax^b

令

U(x)=lnS(x)=lna+blnx U(x)=lnS(x)=lna+blnx

分式拟合

S(x)=xax+b S(x)=\frac{x}{ax+b}

令

U(x)=1S(x)=a+bx U(x)=\frac{1}{S(x)}=a+\frac{b}{x}