跳至主要內容

变换矩阵

大约 25 分钟

变换矩阵

参考自教程 3D 数学基础: 图形与游戏开发

在未明确说明的情况下

  • 以标准基作为默认基底以及变换前后的基底
  • 采用右手系, 以右手定则确定旋转的正方向
  • 角度单位采用角度制
  • 一般向量为列向量

常见线性变换

简单旋转变换

2D 绕原点旋转矩阵

根据使用矩阵表示线性变换中介绍的一般方法, 可以求出 2D 旋转变化的矩阵

当向量逆时针旋转 θ\theta 后标准基有

[10]→[cos⁡θsin⁡θ][01]→[−sin⁡θcos⁡θ] \begin{bmatrix}1\\0\end{bmatrix}\to \begin{bmatrix}\cos\theta\\ \sin\theta\end{bmatrix}\quad \begin{bmatrix}0\\1\end{bmatrix}\to \begin{bmatrix}-\sin\theta\\ \cos\theta\end{bmatrix}

因此有二维绕原点的旋转矩阵

R2(θ)=[cos⁡θ−sin⁡θsin⁡θcos⁡θ] R_{2}(\theta)=\begin{bmatrix}\cos\theta&-\sin\theta\\ \sin\theta&\cos\theta\end{bmatrix}

绕坐标轴旋转矩阵

以绕 xx 轴正方向旋转 θ\theta 为例, 从 yzyz 平面分析, 旋转后标准基有

[100]→[100][010]→[0cos⁡θsin⁡θ][001]→[0−sin⁡θcos⁡θ] \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}\to \begin{bmatrix} 1\\ 0\\ 0\end{bmatrix}\quad \begin{bmatrix} 0\\ 1\\ 0\end{bmatrix}\to \begin{bmatrix} 0\\ \cos\theta\\ \sin\theta\end{bmatrix}\quad \begin{bmatrix} 0\\ 0\\ 1\end{bmatrix}\to \begin{bmatrix} 0\\ -\sin\theta\\ \cos\theta\end{bmatrix}

因此有三维绕 xx 轴旋转矩阵

Rx(θ)=[1000cos⁡θ−sin⁡θ0sin⁡θcos⁡θ] R_{x}(\theta)=\begin{bmatrix}1& 0& 0\\ 0& \cos\theta& -\sin\theta\\ 0& \sin\theta& \cos\theta\end{bmatrix}

类似的绕 yy 与 zz 轴旋转矩阵为

Ry(θ)=[cos⁡θ0sin⁡θ010−sin⁡θ0cos⁡θ]Rz(θ)=[cos⁡θ−sin⁡θ0sin⁡θcos⁡θ0001] R_{y}(\theta)=\begin{bmatrix}\cos\theta& 0& \sin\theta\\ 0& 1& 0\\ -\sin\theta& 0& \cos\theta\end{bmatrix}\quad R_{z}(\theta)=\begin{bmatrix}\cos\theta& -\sin\theta& 0\\ \sin\theta& \cos\theta& 0\\ 0& 0& 1\end{bmatrix}

绕任意轴旋转矩阵

已知旋转轴方向 n⃗\vec{n} 旋转角度 θ\theta 设被旋转向量 v⃗\vec{v}
其中 n⃗\vec{n} 为单位向量

现构造以下向量

  • v⃗\vec{v} 中与旋转轴 n⃗\vec{n} 平行的分量 v⃗∥\vec{v}_{\parallel}, 由向量投影可得其满足 v⃗∥=Pn⃗v⃗=n⃗n⃗Tv⃗\vec{v}_{\parallel}=P_{\vec{n}}\vec{v}=\vec{n}\vec{n}^T\vec{v}
  • v⃗\vec{v} 中与旋转轴 n⃗\vec{n} 垂直的分量 v⃗⊥\vec{v}_{\perp}, 即 v⃗\vec{v} 中除了平行分量以外的部分, 满足 v⃗⊥=v⃗−v⃗∥=v⃗−n⃗n⃗Tv⃗\vec{v}_{\perp}=\vec{v}-\vec{v}_{\parallel}=\vec{v}-\vec{n}\vec{n}^T\vec{v}
  • 同时垂直于 v⃗∥\vec{v}_{\parallel} 与 v⃗⊥\vec{v}_{\perp} 的向量 v⃗p\vec{v}_{p}, 可通过交叉积得到, 满足 v⃗p=n⃗×v⃗⊥=n⃗×(v⃗−v⃗∥)=n⃗×v⃗\vec{v}_{p}=\vec{n}\times\vec{v}_{\perp}=\vec{n}\times(\vec{v}-\vec{v}_{\parallel})=\vec{n}\times\vec{v}

将 v⃗⊥\vec{v}_{\perp} 单位化可得到 n⃗⊥\vec{n}_{\perp}, 将 v⃗∗\vec{v}_{*} 单位化可得到 n⃗∗\vec{n}_{*}
由于 v⃗p\vec{v}_{p} 来自叉乘, 保证了 n⃗⊥\vec{n}_{\perp} 沿 n⃗\vec{n} 的正方向旋转 90∘90^\circ 能得到 n⃗∗\vec{n}_{*}

在旋转的过程中, 于轴平行的分量 v⃗∥\vec{v}_{\parallel} 不变, 仅有垂直分量发生改变, 设旋转后的垂直分量为 v⃗⊥′\vec{v}_{\perp}'
因此旋转后的向量为 v⃗′=v⃗∥+v⃗⊥′\vec{v}'=\vec{v}_{\parallel}+\vec{v}'_{\perp}

在垂直于 n⃗\vec{n} 的平面上建立一个以 u⃗⊥\vec{u}_{\perp} 以及 u⃗∗\vec{u}_{*} 为正方向的坐标系, 可得垂直分量旋转后满足

v⃗⊥′=∣v⃗⊥∣(cos⁡θu⃗⊥+sin⁡θu⃗p) \vec{v}_{\perp}'=|\vec{v}_{\perp}|(\cos\theta\vec{u}_{\perp}+\sin\theta\vec{u}_{p})

注意到, v⃗p\vec{v}_p 与 v⃗⊥\vec{v}_{\perp} 的长度均为 ∣v⃗⊥∣|\vec{v}_{\perp}|, 因此旋转后的向量 v⃗′\vec{v}' 满足

v⃗′=cos⁡θv⃗⊥+sin⁡θv⃗p+v⃗∥ \vec{v}'=\cos\theta\vec{v}_{\perp}+\sin\theta\vec{v}_{p}+\vec{v}_{\parallel}

由于三个构造向量均可以表示为如下的线性变换形式

v⃗∥=Pv⃗=[nx2nxnynxnznxnyny2nynznxnznynznz2]v⃗v⃗⊥=(I−P)v⃗=[1−nx2−nxny−nxnz−nxny1−ny2−nynz−nxnz−nynz1−nz2]v⃗v⃗p=n⃗×v⃗=[n~]v⃗=[0−nznynz0−nx−nynx0]v⃗ \begin{split} \vec{v}_{\parallel}&=P\vec{v}=\begin{bmatrix} n_x^2&n_xn_y&n_xn_z\\ n_xn_y&n_y^2&n_yn_z\\ n_xn_z& n_yn_z& n_z^2 \end{bmatrix}\vec{v}\\ \vec{v}_{\perp}&=(I-P)\vec{v}=\begin{bmatrix} 1-n_x^2&-n_xn_y&-n_xn_z\\ -n_xn_y&1-n_y^2&-n_yn_z\\ -n_xn_z& -n_yn_z& 1-n_z^2 \end{bmatrix}\vec{v}\\ \vec{v}_{p}&=\vec{n}\times\vec{v}=[\tilde{n}]\vec{v}=\begin{bmatrix} 0&-n_z&n_y\\ n_z&0&-n_x\\ -n_y&n_x&0 \end{bmatrix}\vec{v} \end{split}

因此绕轴 n⃗\vec{n} 的变换矩阵可视为以上三个变换矩阵的组合

R(n⃗,θ)=cos⁡θ(I−P)+sin⁡θ[n~]+P R(\vec{n},\theta)=\cos\theta(I-P)+\sin\theta[\tilde{n}]+P

其他简单变换

任意方向缩放矩阵

已知缩放方向 n⃗\vec{n} 缩放倍数 kk, 设被缩放向量 v⃗\vec{v}
其中 n⃗\vec{n} 为单位向量

与旋转类似, 沿任意方向缩放时, 垂直于 n⃗\vec{n} 的分量 v⃗⊥\vec{v}_{\perp} 长度不变, 而平行分量 v⃗∥\vec{v}_{\parallel} 变为原来的 kk 倍, 因此有缩放后的向量 v⃗′\vec{v}' 满足

v⃗′=kv⃗∥+v⃗⊥ \vec{v}'=k\vec{v}_{\parallel}+\vec{v}_{\perp}

可视任一方向投影矩阵为两个投影矩阵的线性组合

S(n⃗,k)=kP+(I−P)=I+(k−1)P S(\vec{n},k)=kP+(I-P)=I+(k-1)P

当缩放倍数为 −1-1 时, 即为沿特定方向的镜像

任意平面的正交投影

已知缩放方向 n⃗\vec{n} (直线方向或平面法向量), 设被投影向量 v⃗\vec{v}
其中 n⃗\vec{n} 为单位向量

投影到直线时, 即仅留下平行于方向向量的分量 v⃗∥\vec{v}_{\parallel}, 因此投影到直线的变换即投影矩阵

Pl(n⃗)=n⃗n⃗T P_l(\vec{n})=\vec{n}\vec{n}^T

投影到平面时, 即除去平行于法向量的分量 v⃗∥\vec{v}_{\parallel}, 剩余垂直分量, 因此投影到平面的变换矩阵

Pp(n⃗)=I−Pl(n⃗) P_p(\vec{n})=I-P_l(\vec{n})

线性变换的组合

以下结论均以默认使用列向量时得出
如果使用行向量, 则可通过转置得到类似的结论

线性变换的组合规则

由线性变换的规则可得, 对于线性变换 y⃗=T(x⃗)\vec{y}=T(\vec{x}) 等价于 y⃗=Ax⃗\vec{y}=A\vec{x}
因此通过多个线性变换矩阵相乘, 即可实现变换的组合
但是, 由矩阵乘法规则可得, 矩阵乘法满足结合律, 不满足交换律
因此对于组合变换矩阵 C=BAC=BA, 相当于先进行变化 AA, 再进行变换 BB
注意在这个过程中, 基底保持不变, 且变换均是相对基底进行的

4x4 齐次矩阵

齐次坐标

齐次坐标系的定义

齐次坐标系 (homogeneous coordinates) 又称为投影坐标系, 与一般的笛卡尔坐标系不同, 在 nn 维空间中, 除了一般的 nn 个坐标轴, 还有一个齐次坐标轴 ww
因此齐次坐标系中的向量 v⃗h\vec{v}_{h} 共有 n+1n+1 个坐标值

而在齐次坐标系中补充的齐次坐标轴的本质为一个投影系数, 对于齐次坐标系中的向量 v⃗h=[v⃗′w]\vec{v}_{h}=\begin{bmatrix}\vec{v}'\\ w\end{bmatrix}, 对应为笛卡尔坐标系中的向量 v⃗=v⃗′/w\vec{v}=\vec{v}'/w

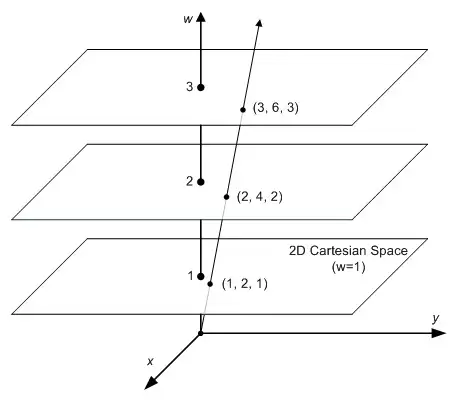
如图所示, 笛卡尔坐标系即齐次坐标系中, w=1w=1 的一个平面, 齐次坐标系中的点通过一条过原点的直线投影到 w=1w=1 的平面上

例如三维齐次空间中的向量 v⃗=[xyw]T\vec{v}=\begin{bmatrix}x&y&w\end{bmatrix}^T 经过映射后对应的是二维实际空间向量 v⃗h=[xwyw]T\vec{v}_h=\begin{bmatrix}\frac{x}{w}&\frac{y}{w}\end{bmatrix}^T

特别的, 当齐次空间向量 v⃗\vec{v} 在齐次坐标的分量为 00 时, 表示该向量位于无穷远处, 此时投影到实际空间的向量表示的是一个在 v⃗′\vec{v}' 方向的, 且长度为 ∞\infty 的向量

齐次坐标系下的线性变换

对于实际空间中的任意线性变换 TT, 由于实际空间的线性变换与齐次坐标无关, 因此实际空间的线性变换矩阵 AA 在齐次空间中的形式为

Ah=[A0⃗0⃗T1] A_h=\begin{bmatrix}A&\vec{0}\\\vec{0}^T&1\end{bmatrix}

平移变换

在笛卡尔坐标系中, 平移变换不满足线性变换的要求, 因此也无法使用一个线性变换矩阵表示
此外笛卡尔坐标系的变换都要求以原点为中心进行, 不能在原点之外的位置进行变换

为了使用线性变换矩阵表示, 并且使用矩阵相乘即可叠加, 矩阵求逆即为相反变换等优点, 现引入齐次空间
因为在齐次空间中的平移变换属于线性变换

无穷远点的平移

在介绍平移矩阵变换之前, 首先要明确
在齐次坐标系中, 对于无穷远处的向量 v⃗h1\vec{v}_{h1}, 即 w=0w=0, 与任何有限的向量 v⃗h2\vec{v}_{h2} 相加, 结果依然为 v⃗h1\vec{v}_{h1}

因此无穷远处的点始终不会受平移变换的影响

平移变换矩阵

已知平移方向 t⃗=[ΔxΔyΔz]T\vec{t}=\begin{bmatrix}\Delta x&\Delta y&\Delta z\end{bmatrix}^T

注意到齐次坐标系中的标准基 v⃗1=[1000]T\vec{v}_1=\begin{bmatrix}1& 0& 0& 0\end{bmatrix}^T 表示一个 xx 正方向的, 位于无穷远处的向量, 因此即使经过平移, 其坐标也不会改变, 有 T(v⃗1)=v⃗1T(\vec{v}_1)=\vec{v}_1
对于另外两个在实际坐标轴上的标准基同理

而在齐次坐标轴上的标准基 v⃗4=[0001]T\vec{v}_4=\begin{bmatrix}0& 0& 0& 1\end{bmatrix}^T, 对应了笛卡尔坐标系中的原点, 因此在平移后有 T(v⃗4)=[ΔxΔyΔz1]TT(\vec{v}_4)=\begin{bmatrix}\Delta x&\Delta y&\Delta z& 1\end{bmatrix}^T

因此, 齐次坐标系中的平移变换矩阵为

T(t⃗)=[100Δx010Δy001Δz0001] T(\vec{t})= \begin{bmatrix} 1& 0& 0& \Delta x\\ 0& 1& 0& \Delta y\\ 0& 0& 1& \Delta z\\ 0& 0& 0& 1 \end{bmatrix}

显然平移变换矩阵的逆为

T−1(t⃗)=T(−t⃗)=[100−Δx010−Δy001−Δz0001] T^{-1}(\vec{t})=T(-\vec{t})= \begin{bmatrix} 1& 0& 0& -\Delta x\\ 0& 1& 0& -\Delta y\\ 0& 0& 1& -\Delta z\\ 0& 0& 0& 1 \end{bmatrix}

仿射变换

将形如 TA(x⃗)=Ax⃗+t⃗T_A(\vec{x})=A\vec{x}+\vec{t} 的变换称为仿射变换
仿射变换是线性变换的一个超集, 因为其中还包含了坐标系的平移
例如以原点外的直线为轴的旋转, 投影到不过原点的平面

利用齐次坐标系与平移变换, 可以将这些过原点的线性变换转化为不过原点的仿射变换
仅需利用线性变换矩阵的逆, 先将坐标系平移, 经线性变换后, 再将坐标系复原到标准基上

假设以位置 p⃗\vec{p} 为变换中心进行线性变换 AA, 则有齐次坐标系下的仿射变换矩阵

Ap=T(p⃗)AT−1(p⃗) A_{p}=T(\vec{p})AT^{-1}(\vec{p})

三维旋转变换的表示

基本概念

方位与方向的区别

在三维空间中

由于向量没有厚度, 因此向量绕自身旋转并不会改变向量的效果
因此向量只有方向而没有方位, 仅需两个值即可表示向量的方向 (极坐标)

对于有厚度的物体, 除了确定物体的方向, 还应确定自转, 并构成方位
因此至少要三个参数才能表示一般物体的方位

方位与角位移

与位移类似, 旋转的本质也是两个坐标系之间的变换, 因此旋转的程度必须相对于某个特定的基底才能描述

习惯上使用方位表示物体相对标准基底的旋转变换, 角位移表示物体由一个方位到下一个方位之间的旋转变换

方位与角位移本质时相同的, 只是使用场合不同

旋转矩阵

已知旋转属于线性变换, 因此可以使用旋转变换的变换矩阵来表示旋转的方位

旋转矩阵有优点

  • 如果要具体计算物体旋转后的状态, 必须借助旋转矩阵
  • 通过矩阵的相乘能够很好地与其他线性变换 / 旋转变换组合

但是旋转矩阵也存在以下缺点

  • 直接使用旋转矩阵表示方位时, 一个方位需要 99 个参数, 然而描述方位时实际只需要 33 个参数
  • 旋转矩阵要求矩阵三个列向量必须为单位向量且相互正交, 因此在组合时必须时刻对旋转矩阵标准正交化, 以防止浮点误差导致旋转矩阵蠕变, 使矩阵包含了缩放, 镜像等操作
  • 旋转矩阵并不直观

旋转矩阵的标准化

参考 https://zhuanlan.zhihu.com/p/665225211open in new window

奇异值 σi\sigma_i 反映了坐标轴的拉伸与镜像, 显然旋转变换不会对坐标轴产生影响
因此旋转矩阵的奇异值必定为 σi=1\sigma_i = 1, 有 Σ=I\Sigma=I

当旋转矩阵因舍入问题蠕变时, 实质即其中被引入了缩放等额外的变换, 此时 σi≠1\sigma_i\neq 1
通过求出蠕变旋转矩阵 R′R' 的奇异值分解 UΣ′VTU\Sigma' V^T, 令 Σ′=I\Sigma'=I, 即 R=UVTR=UV^T 即可标准化旋转矩阵
这其中的运算量显然大于标准化四元数

欧拉角

将旋转分解到三个相互垂直轴上描述都可以称为欧拉角
因此仅需要三个参数就可以描述方位或角位移

欧拉角系统约定

理论上分解到任意三个正交轴, 任意旋转顺序都属于欧拉角
在实际中一般使用如下方式建立标准基底的三个轴, 且采用以下两种欧拉角系统

规定采用右手系, 假设有一个位于初始方向的物体

  • 以物体的质心为原点
  • 以垂直底面向上为 xx 轴的正方向
  • 一般以平行于物体的正前方或水平向右为 zz 轴正方向
  • 一般以垂直于物体的正前方或垂直纸面向里为 yy 轴正方向

定义绝对坐标系, 观察坐标系与物体坐标系

  • 物体坐标系始终相对物体静止
  • 物体的坐标以观察坐标系为基底
  • 绝对坐标系为一个便于说明的参照, 无实际意义

初始状态下, 绝对坐标系, 观察坐标系与物体坐标系重合,

  • zyxzyx 约定
    • 首先绕物体坐标系的 zz 轴旋转 (此时两个坐标系重合), 即物体绕自身主轴旋转
    • 然后绕物体坐标系的 yy 轴旋转 (此时物体坐标系已经发生改变), 即物体绕垂直于主轴方向旋转
    • 最后绕物体坐标系的 xx 轴旋转, 即垂直于剩余两轴方向旋状
  • rpyrpy 约定 (roll-pitch-yaw)
    • 首先绕观察坐标系的 xx 轴旋转, 称为 roll, 滚动角
    • 然后绕观察坐标系的 yy 轴旋转, 称为 pitch, 俯仰角
    • 最后绕观察坐标系的 zz 轴旋转, 称为 yaw, 航向角
  • zyzzyz 约定

由欧拉角得到旋转矩阵

对于 rpyrpy 约定, 由于始终以观察坐标系为旋转轴, 因此直接组合绕坐标轴旋转矩阵即可, 其旋转矩阵满足

R(r,p,y)=Rz(y)Ry(p)Rx(r) R(r,p,y)=R_z(y)R_y(p)R_x(r)

对于 zyxzyx 约定, 为了实现相对物体坐标系的旋转, 可通过旋转观察坐标系的方式实现. 由于物体坐标系与绝对坐标系始终重合, 因此将观察坐标系相对绝对坐标系的坐标轴旋转也等价于其相对于物体坐标系的坐标轴
除了旋转观察坐标系, 还需要将原始坐标 (以绝对坐标系为基底) 的基底变换到观察坐标系上

R(z,y,x)=[Rx(−x)Ry(−y)Rz(−z)]−1=Rz(z)Ry(y)Rx(x) R(z,y,x)=[R_x(-x)R_y(-y)R_z(-z)]^{-1}=R_z(z)R_y(y)R_x(x)

对于 zyzzyz 约定, 与 zyxzyx 约定类似, 有

R(z,y,z′)=[Rz(−z′)Ry(−y)Rz(−z)]−1=Rz(z)Ry(y)Rz(z′) R(z,y,z')=[R_z(-z')R_y(-y)R_z(-z)]^{-1}=R_z(z)R_y(y)R_z(z')

无论旋转方式如何, 通过形似 xyzxyz 或 zyzzyz 的方式组合旋转矩阵, 无论相对旋转对象如何, 共有 1212 种不同的欧拉角表示方式

欧拉角的特点

欧拉角有优点

  • 欧拉角只需要三个数就能表示方位
  • 欧拉数中任意三个数都是合法的 (但需要明确角度制还是弧度制)
  • 欧拉角能直观地反应方位

欧拉角有缺点

  • 存在无数种欧拉角的组合能够表达同一个方位, 因此一般限制 r,y∈(−180∘,180∘],p∈(−90∘,90∘]r,y\in(-180^\circ,180^\circ],p\in(-90^\circ,90^\circ], 例如 p=135∘p=135^\circ 与 r=180∘,p=45∘,y=180∘r=180^\circ,p=45^\circ,y=180^\circ 表达的方位相同
  • 此外还将导致欧拉角不易进行插值, 例如 720∘→60∘720^\circ\to 60^\circ 的插值将导致额外的旋转
  • 当 p=±90∘p=\pm 90^\circ 时, 将出现万向锁问题, 这将导致航向角 yaw 失效

四元数

关于四元数的基础见四元数的基础介绍

注意四元数在表示方位 / 角位移时, 默认为单位四元数, 因此存在关系

w2+x2+y2+z2=1 w^2+x^2+y^2+z^2=1

由四元数得到旋转矩阵

通过将四元数转为轴角对, 注意到单位四元数与轴角对的参数存在以下关联

  • w=cos⁡(θ/2)w=\cos(\theta/2)
  • sin⁡(θ/2)=x2+y2+z2=1−w2\sin(\theta/2)=\sqrt{x^2+y^2+z^2}=\sqrt{1-w^2}
  • nx=xsin⁡(θ/2)=xx2+y2+z2n_x=\frac{x}{\sin(\theta/2)}=\frac{x}{\sqrt{x^2+y^2+z^2}}, ny,nzn_y,n_z 类似

通过绕任意轴旋转矩阵即可将四元数转为旋转矩阵

R(q)=[1−2y2−2z22xy−2wz2xz+2wy2xy+2wz1−2x2−2z22yz−2wx2xz−2wy2yz+2wx1−2x2−2y2] R(q)=\begin{bmatrix} 1-2y^2-2z^2&2xy-2wz&2xz+2wy\\ 2xy+2wz&1-2x^2-2z^2&2yz-2wx\\ 2xz-2wy&2yz+2wx&1-2x^2-2y^2 \end{bmatrix}

由旋转矩阵得到四元数

根据单位四元数的特点, 通过不同方式组合旋转矩阵对角线上的元素有

m11+m22+m33=4w2−1m11−m22−m33=4x2−1−m11+m22−m33=4y2−1−m11−m22+m33=4z2−1 \begin{split} m_{11}+m_{22}+m_{33}&=4w^2-1\\ m_{11}-m_{22}-m_{33}&=4x^2-1\\ -m_{11}+m_{22}-m_{33}&=4y^2-1\\ -m_{11}-m_{22}+m_{33}&=4z^2-1 \end{split}

注意, 以上公式无法判断系数的正负负号, 因此一般仅用以上公式计算求出其中一个系数
实际使用中, 将计算四个系数中, 绝对值最大的一个 (即 4m2−14m^2-1 最大, 比较时不需要具体确定系数值)

之后, 通过将旋转矩阵相对对角线对称的两个元素相加或相减, 即可得到任意两个四元数元素之积, 通过此方法求出剩余系数

由欧拉角得到四元数

由四元数得到欧拉角

四元数的特点

四元数有优点

  • 仅四元数有简单平滑插值的方法, 另外两种表示方法则没有
  • 四元数的标准乘法能快速组合多个旋转, 运算速度快于矩阵
  • 四元数仅占用四个数, 仅稍大于欧拉角

四元数有缺点

  • 由于运算精度, 四元数可能不合法, 需要对四元数进行标准化
  • 四元数仅能相对观察坐标系进行旋转, 无法像矩阵能够对惯性坐标系进行旋转
  • 四元数并不直观, 需要转为轴角对或欧拉角

四元数介绍

四元数表示与基本性质

四元数基本运算法则

四元数与复数类似, 但存在三个虚数单位 i,j,k\bm{i},\bm{j},\bm{k}, 并且有运算法则

i2=j2=k2=−1ij=k,ji=−kjk=i,kj=−iki=j,ik=−j \begin{split} &\bm{i}^2=\bm{j}^2=\bm{k}^2=-1\\ &\bm{i}\bm{j}=\bm{k},\bm{j}\bm{i}=-\bm{k}\\ &\bm{j}\bm{k}=\bm{i},\bm{k}\bm{j}=-\bm{i}\\ &\bm{k}\bm{i}=\bm{j},\bm{i}\bm{k}=-\bm{j} \end{split}

四元数表示方式

由三个虚数单位分别乘以一个实数, 并与一个实数共同组成四元数

q=w+xi+yj+zk q=w+x\bm{i}+y\bm{j}+z\bm{k}

此外也常用如下方式表示一个四元数

q=[w(xyz)]=[wv⃗] q=\begin{bmatrix}w&(x&y&z)\end{bmatrix}=\begin{bmatrix}w&\vec{v}\end{bmatrix}

四元数与轴角对

轴角对

欧拉已经证明, 任意三维中的旋转组合, 均等价于一个绕特定轴的旋转
因此可使用旋转轴方向的单位向量 n⃗\vec{n} 与旋转角度 θ\theta 表示旋转变换
四元数也可视为轴角对的一种特殊表示方式
其与轴角对的参数 θ,n⃗\theta,\vec{n} 之间满足

q=[cos⁡(θ/2)(sin⁡(θ/2)nxsin⁡(θ/2)nysin⁡(θ/2)nz)]=[cos⁡(θ/2)sin⁡(θ/2)n⃗] q=\begin{bmatrix}\cos(\theta/2)&(\sin(\theta/2)n_x&\sin(\theta/2)n_y&\sin(\theta/2)n_z)\end{bmatrix}=\begin{bmatrix}\cos(\theta/2)&\sin(\theta/2)\vec{n}\end{bmatrix}

与欧拉角不同, 四元数的插值旋转永远走最短圆弧, 例如当旋转角度 θ=240∘\theta=240^\circ, 则通过插值旋转路径为 0→−120∘0\to -120^\circ

共轭四元数

与复数类似, 四元数的共轭 q∗q^* 与模长 ∥q∥\begin{Vmatrix}q\end{Vmatrix} 满足

q∗=[w−v⃗]=[w(−x−y−z)] q^*=\begin{bmatrix}w&-\vec{v}\end{bmatrix}=\begin{bmatrix}w&(-x&-y&-z)\end{bmatrix}

∥q∥=w2+∥v∥2=w2+x2+y2+z2 \begin{Vmatrix}q\end{Vmatrix}=\sqrt{w^2+\begin{Vmatrix}v\end{Vmatrix}^2}=\sqrt{w^2+x^2+y^2+z^2}

注意到, 当轴角对以四元数的方式表示时

∥q∥=cos⁡(θ/2)2+sin⁡(θ/2)∥v∥2=1 \begin{Vmatrix}q\end{Vmatrix}=\sqrt{\cos(\theta/2)^2+\sin(\theta/2)\begin{Vmatrix}v\end{Vmatrix}^2}=1

四元数与轴角对的性质

因此

  • 如果四元数要表示为一个合法的方位 / 角位移时, 其模长必须为 11, 也称为单位四元数
  • 对于一个四元数 q∗q^* , 其共轭相当于将角度 θ\theta 取反, 因此其共轭反映了一个相反效果的变换 q∗q^*
  • 而将四元数取负 −q-q, 相当于将旋转轴与旋转角度同时取反, 旋转效果与未取反的四元数相同, 因此任意方位都存在两种不同的表达方式 qq 与 −q-q
  • 当轴角对的 θ=0\theta=0, 则四元数为 q=[10⃗]q=\begin{bmatrix}1&\vec{0}\end{bmatrix}, 该四元数不反映任何旋转, 因此称为标准四元数

四元数乘法运算

标准乘法定义

对于任意四元数 q1,q2q_1,q_2, 与复数乘法类似, 定义四元数的叉乘 (也是四元数的标准乘法)

q1q2=(w1+x1i+y1j+z1k)(w2+x2i+y2j+z2k)=[w1v⃗1][w2v⃗2]=[w1w2−v⃗1v⃗2w1v⃗2+w2v⃗1−v⃗1×v⃗2] \begin{split}q_1q_2&=(w_1+x_1\bm{i}+y_1\bm{j}+z_1\bm{k})(w_2+x_2\bm{i}+y_2\bm{j}+z_2\bm{k})\\ &=\begin{bmatrix}w_1&\vec{v}_1\end{bmatrix}\begin{bmatrix}w_2&\vec{v}_2\end{bmatrix}\\ &=\begin{bmatrix}w_1w_2-\vec{v}_1\vec{v}_2&w_1\vec{v}_2+w_2\vec{v}_1-\vec{v}_1\times\vec{v}_2\end{bmatrix}\end{split}

四元数乘法的本质即连接了两个角位移

四元数标准乘法的运算法则

由标准乘法中涉及到的叉乘可得, 四元数的标准乘法满足结合律, 但不满足交换律

{(q1q2)q3=q1(q2q3)q1q2≠q2q1 \begin{cases} &(q_1q_2)q_3=q_1(q_2q_3)\\ &q_1q_2\neq q_2q_1 \end{cases}

易得, 四元数乘积的模长等于两个四元数模长的乘积

∥q1q2∥=∥q1∥∥q2∥ \begin{Vmatrix}q_1q_2\end{Vmatrix}=\begin{Vmatrix}q_1\end{Vmatrix}\begin{Vmatrix}q_2\end{Vmatrix}

四元数的逆与方位间角位移

四元数 qq 乘以其共轭 q∗q^* 后可得到 qq∗=∥q∥qq^*=\begin{Vmatrix}q\end{Vmatrix}

以此定义四元数的逆满足 qq−1=1qq^{-1}=1
可得四元数的逆表达式为如下

q−1=q∗∥q∥ q^{-1}=\frac{q^{*}}{\begin{Vmatrix}q\end{Vmatrix}}

易得, 对于多个四元数相乘的逆有

(q1q2)−1=q2−1q1−1 (q_1q_2)^{-1}=q_2^{-1}q_1^{-1}

已知方位 q1q_1 与 q2q_2, 其中方位 q1q_1 经过角位移 dd 得到 q2q_2, 则有 (注意四元数乘法不满足交换律, 且角位移结合顺序为从右向左)

dq1=q2d=q2q1−1 \begin{split} dq_1&=q_2\\ d&=q_2q_1^{-1} \end{split}

其中的 dd 为方位 q1q_1 到方位 q2q_2 的角位移

四元数与旋转

对于向量 v⃗\vec{v}, 定义四元数 pv=[0v⃗]p_v=\begin{bmatrix}0&\vec{v}\end{bmatrix} 来表示这一向量
设对于来自轴角对 θ,n⃗\theta,\vec{n} 的四元数 aa, 将 v⃗\vec{v} 绕 n⃗\vec{n} 旋转 θ\theta 度得到向量 u⃗\vec{u}
则对于表示 u⃗\vec{u} 的四元数 quq_u 满足

pu=apva−1 p_u=ap_va^{-1}

显然, 当对 pup_u 再进行一次旋转 bb 得到 p′p', 等价于先旋转 aa, 再旋转 bb 的组合

p′=(ba)pv(a−1b−1)=(ba)pv(ba)−1 p'=(ba)p_v(a^{-1}b^{-1})=(ba)p_v(ba)^{-1}

因此与矩阵类似, 通过左乘四元数 qq, 可以以从右到左的顺序连接多个四元数
四元数表示角位移时, 连接顺序为从右向左 (观察坐标系不变)

有的时候也将重新定义四元数的乘法为

q1q2=[w1w2−v⃗1v⃗2w1v⃗2+w2v⃗1+v⃗1×v⃗2] q_1q_2=\begin{bmatrix}w_1w_2-\vec{v}_1\vec{v}_2&w_1\vec{v}_2+w_2\vec{v}_1+\vec{v}_1\times\vec{v}_2\end{bmatrix}

此时通过四元数分别完成旋转 a,ba,b 的表达式变为 q=(ab)pv(ab)−1q=(ab)p_v(ab)^{-1}

四元数的其他运算

四元数的点乘

将四元数的四个参数视为一个 R4R^4 向量
四元数 q1q2q_1q_2 的点乘即这两个向量之间点乘, 得到一个实数

q1⋅q2=w1w2+v⃗1⋅v⃗2 q_1\cdot q_2=w_1w_2+\vec{v}_1\cdot\vec{v}_2

当 q1,q2q_1,q_2 为单位四元数时, 显然 −1≤q1⋅q2≤1-1\le q_1\cdot q_2\le 1
当两个四元数点乘乘积的绝对值越接近 11, 表明两个四元数越相近 (相反的四元数表示的旋转相同)

四元数的对数函数

与复数的对数运算类似, 对于单位四元数 q=[cos⁡(θ/2)sin⁡(θ/2)n⃗]q=\begin{bmatrix}\cos(\theta/2)&\sin(\theta/2)\vec{n}\end{bmatrix}, 其对数函数满足

log⁡q=[0θ2n⃗] \log q=\begin{bmatrix}0&\frac{\theta}{2}\vec{n}\end{bmatrix}

单位四元数经过对数函数, 能够提取四元数中的轴角对信息

四元数的指数函数

四元数的指数函数即对数函数的逆运算, 对于 w=0w=0 的四元数 q=[0θ2n⃗]q=\begin{bmatrix}0&\frac{\theta}{2}\vec{n}\end{bmatrix}, 其指数函数满足

exp⁡q=[cos⁡(θ2)sin⁡(θ2)n⃗] \exp q=\begin{bmatrix}\cos(\frac{\theta}{2})&\sin(\frac{\theta}{2})\vec{n}\end{bmatrix}

w=0w=0 的四元数 (轴角对) 经过指数函数, 能够转换为单位四元数

四元数的幂

已知四元数的对数与指数函数后, 根据对数与指数函数的性质, 即可定义四元数的幂满足

qk=exp⁡(klog⁡q) q^{k}=\exp(k\log q)

由此可得, 与复数类似, 对于四元数 qq 的 kk 次幂相当于将原旋转角度乘以 kk 倍
注意 kk 可以是任意实数, 如 q−1/3q^{-1/3} 将表示一个绕相同轴的旋转, 但旋转角度为原来的 13\frac{1}{3}, 且旋转方向相反

四元数两点插值与样条插值

四元数插值 Slerp

slerpslerp 即球面线性插值, 是一种基于四元数的, 在两个旋转之间平滑线性插值的最优运算
slerpslerp 的本质为一个三元函数 qt=slerp(q1,q2,t)q_t=slerp(q_1,q_2,t)
其中 q1,q2q_1,q_2 为起始与结束方位的四元数, tt 为一个 (0,1)(0,1) 的比例值, 表示中间位置, 结果 qtq_t 为插值结果
物体沿两个方位间的 slerpslerp 插值旋转运动时能保证其角速度始终不变

根据线性插值思想

  • 计算首尾两个值的差
  • 将初始值加上首尾差乘上比例值, 得到插值结果

因此根据四元数的方位间角位移与幂运算可得
首先求出方位间角位移计算首尾方位的角位移, 然后通过求 tt 的幂, 得到部分角位移, 最后与初始位置的方位连接得到插值结果

slerp(q1,q2,t)=(q2q1−1)tq1 slerp(q_1,q_2,t)=(q_2q_1^{-1})^{t}q_1

可得, slerpslerp 的本质即沿 q1,q2q_1,q_2 构成的最短圆弧上进行线性插值, 插值结果即圆弧上的各个点
实际应用中, 由于合法方位均为单位四元数, 因此可将单位四元数 q1,q2q_1,q_2 视为两个长度为 11 的 R4R^4 向量, 插值结果在 r=1r=1 的四维圆弧上

为了方便理解与推导, 将 q1,q2q_1,q_2 视为二维单位圆上的两条半径上的向量, 插值结果为这两个向量的线性组合 qt=k1q1+k2q2q_t=k_1q_1+k_2q_2
如图所示

QH=k1sin⁡(ω)=1sin⁡(tω)→k1=sin⁡(tω)sin⁡(ω) QH=k_1\sin(\omega)=1\sin(t\omega)\\ \to k_1=\frac{\sin(t\omega)}{\sin(\omega)}

同理可得 k2=sin⁡[(1−t)ω]sin⁡(ω)k_2=\frac{\sin[(1-t)\omega]}{\sin(\omega)} (调换 q1,q2q_1,q_2 即可得), 其中 q1⋅q2=1⋅1cos⁡ωq_1\cdot q_2=1\cdot 1\cos\omega
因此对于单位四元数 q1,q2q_1,q_2 有球面插值

qt=sin⁡(tω)sin⁡(ω)q1+sin⁡[(1−t)ω]sin⁡(ω)q2 q_t=\frac{\sin(t\omega)}{\sin(\omega)}q_1+\frac{\sin[(1-t)\omega]}{\sin(\omega)}q_2

在以上针对单位四元数的球面插值在具体实现时需要注意

  • 由于 q1,q2q_1,q_2 的方向不同可能对应两个不同的插值圆弧, 为了保持最小圆弧, 应保证 q1⋅q2≥0q_1\cdot q_2\ge 0, 若不满足则取 q1=−q1q_1=-q_1 (注意四元数取反并不会改变旋转效果)
  • 当 q1,q2q_1,q_2 非常接近时, ω,sin⁡ω≈0\omega,\sin\omega\approx 0, 这不利于除法运算, 因此可改为向量 q1,q2q_1,q_2 四个元素的线性插值代替球面插值

四元数样条 Squad

对于两个方位之间的移动, slerpslerp 能够保证角速度不变, 但对于多个方位之间的移动, 各段方位之间的角速度将产生突变
以下介绍四元数样条算法 squadsquad (Spherical and Quadrangle), 该样条算法能保证轨迹的角速度连续可导, 但角速度不再是不变的

已知各个控制点的方位构成一个四元数序列 q1,q2,…,qnq_1,q_2,\dots,q_n
现引入辅助控制点的方位序列 s1,s2,…,sns_1,s_2,\dots,s_n
其中的辅助控制点的方位满足

si=qiexp⁡(−log⁡(qi−1qi+1)+log⁡(qi−1qi−1)4) s_i=q_i\exp(-\frac{\log(q_i^{-1}q_{i+1})+\log(q_i^{-1}q_{i-1})}{4})

注意到, 由于 q0,qn+1q_0,q_{n+1} 未定义, 因此辅助控制点方位 s1,sns_1,s_n 无法确定, 一般规定 q0=q1,qn+1=qnq_0=q_1,q_{n+1}=q_n

现对于序列中相邻的两个控制点 qi,qi+1q_i,q_{i+1}, 设控制点间的比例值为 hh, 则这两个控制点之间的样条插值结果为

squad(qi,qi+1,h)=slerp[slerp(qi,qi+1,h),slerp(si,si+1,h),2h(1−h)] squad(q_i,q_{i+1},h)=slerp[slerp(q_i,q_{i+1},h),slerp(s_i,s_{i+1},h),2h(1-h)]