跳至主要內容

运动学

大约 13 分钟

运动学

质点运动学

自然坐标系

设质点轨迹的指向运动方向的切向为 τ⃗\vec{\tau}, 指向曲率圆心的法向 n⃗\vec{n}, 将 τ⃗,n⃗\vec{\tau},\vec{n} 构成的坐标系称为自然坐标系

速度表示

自然坐标系下, τ⃗\vec{\tau} 即速度的方向, 因此 v⃗=vτ⃗\vec{v}=v\vec{\tau}

加速度分解

自然坐标系下, 加速度可分解为切向加速度 ata_t 与法向加速度 ana_n, 根据微分关系可表示为

a⃗=atτ⃗+ann⃗=dvdtτ⃗+v2ρn⃗ \vec{a}=a_t\vec{\tau}+a_n\vec{n}=\frac{dv}{dt}\vec{\tau}+\frac{v^2}{\rho}\vec{n}

其中 vv 为速度的大小, 不是矢量; ρ\rho 为轨迹的曲率半径, 可通过此方法求出运动轨迹的曲率半径

点运动的合成

将点的运动向静系和动系分解, 可得到三种运动

  1. 绝对运动 (absolution) 动点相对于静系的运动
  2. 相对运动 (relation) 动点相对于动系的运动
  3. 牵连运动 (entrainment) 动系相对于静系的运动

解题时必须明确指出所选择的动系与计算的动点

速度合成定律

va⃗=vr⃗+ve⃗ \vec{v_a}=\vec{v_r}+\vec{v_e}

加速度合成定律

加速度合成时, 如果动系不是平动 ω=0\omega=0 , 还要考虑科氏加速度 ak⃗=2ω⃗×vr⃗\vec{a_k}=2\vec{\omega}\times\vec{v_r} 的影响

a⃗=ar⃗+ae⃗+2ω⃗×vr⃗ \vec{a}=\vec{a_r}+\vec{a_e}+2\vec{\omega}\times\vec{v_r}

动系动点的选择

  1. 动点为两个框体的交点时, 分别以两个框体为动系, 联立方程
  2. 没有稳定接触点时, 使用刚体的平面运动
  3. 有稳定接触点时, 动系的选择
    1. 动点不能在动系上, 否则无意义
    2. 动系最好与题目有关 (求动系的 ω\omega )
    3. 动点轨迹易求
    4. 动系平动 (避免求科氏加速度)
  4. 动点选择
    1. 套筒
    2. 铰链
    3. 圆心
    4. 杆的一端

例题

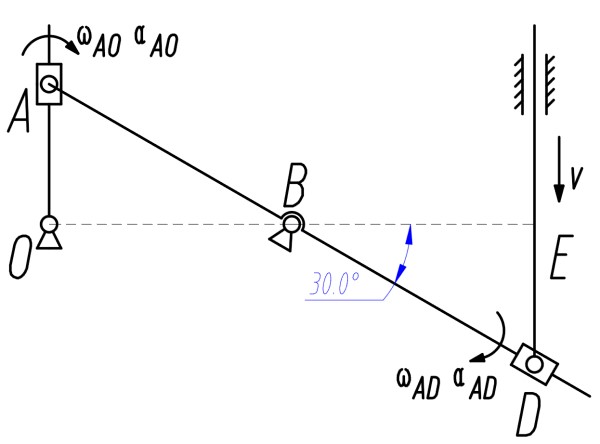
杆 DEDE 以 vv 沿垂直滑道匀速下滑, 图示瞬间, 杆 OAOA 垂直, AB=BD=2r,OA∥EDAB=BD=2r,OA\parallel ED. 求此时杆 OAOA 的角速度和角加速度

几何关系确定

  • 依题意得有

AB=BD=2r AB=BD=2r

  • 如图所示角度满足

∠ABO=∠DBE=30∘,∠OAB=60∘ \angle ABO=\angle DBE=30^\circ,\angle OAB=60^\circ

  • OAOA 段长度有

OA=ABsin⁡30∘ OA=AB\sin 30^\circ

速度分析

在速度分析前先规定机构中杆件角速度的正方向, 也可以统一采用逆时针, 便于判断科氏力的方向

从具有已知量的部分开始分析, 以未知部分杆 ABAB 为动系, 稳定接触点铰链 DD 为动点

动点 DD 为杆 DEDE 的一端, 且杆 DEDE 匀速平动, 因此其绝对速度即杆 DEDE 的平动速度, 方向向下, 有

vD=v v_D=v

动系杆 ADAD 绕铰链 BB 转动, 因此动系上 DD 处的点的速度 (牵连速度) 方向垂直于杆, 大小满足

vDe=BDωAD=2rωAD v_D^e=BD\omega_{AD}=2r\omega_{AD}

假设动系静止, 动点 DD 所在的套筒只能沿杆 ADAD 平动, 因此在此瞬间, 动点 DD 的相对速度沿杆方向, 大小未知

确定几个速度分量的几何关系后画出动点 DD 速度简图

根据速度合成定律有

vD⃗=vDe⃗+vDr⃗ \vec{v_D}=\vec{v_D^e}+\vec{v_D^r}

由于 vDe⃗\vec{v_D^e} 与 vDr⃗\vec{v_D^r} 方向垂直, 因此可将矢量沿这两个方向分别分解得到

vDe=vDcos⁡30∘=32v v_D^e=v_D\cos 30^\circ=\frac{\sqrt{3}}{2}v

vDr=vDsin⁡30∘=12v v_D^r=v_D\sin 30^\circ=\frac{1}{2}v

根据 vDe⃗\vec{v_D^e} 与 ωAD\omega_{AD} 的关系还可以得到

ωAD=3v4r \omega_{AD}=\frac{\sqrt{3}v}{4r}

从已知部分逐步分析到待求部分, 以待求部分杆 AOAO 为动系, 稳定接触点铰链 AA 为动点

分别分析三个速度可得到如图方向关系与以下代数关系

vAe=ωAO v_A^e=\omega_{AO}

vA=ABωAD=2rωAD=3v2 v_A=AB\omega_{AD}=2r\omega_{AD}=\frac{\sqrt{3}v}{2}

确定几个速度分量的几何关系后画出动点 AA 速度简图

根据速度合成定律

vA⃗=vAe⃗+vAr⃗ \vec{v_A}=\vec{v_A^e}+\vec{v_A^r}

分别沿 xx, yy 轴方向 (vAe⃗,vAr⃗\vec{v_A^e},\vec{v_A^r} 方向) 分解可得

vAr=vAcos⁡30∘=34v v_A^r=v_A\cos 30^\circ=\frac{3}{4}v

vAe=vAsin⁡30∘=34v v_A^e=v_A\sin 30^\circ=\frac{\sqrt{3}}{4}v

根据 vAe⃗\vec{v_A^e} 与 ωAO\omega_{AO} 的关系还可以得到

ωAO=3v4r \omega_{AO}=\frac{\sqrt{3}v}{4r}

加速度分析

按原先速度分析的顺序对加速度进行分析

由于杆 DEDE 匀速运动, 因此动点 DD 的绝对加速度满足

aD=0 a_D=0

杆 ADAD 上的点 DD 绕铰链 BB 旋转, 因此需要将牵连加速度 aDe⃗\vec{a_D^e} 按自然坐标系分解为法向 aDen⃗\vec{a_D^{en}} 与切向 aDeτ⃗\vec{a_D^{e\tau}}, 其中

  • 切向加速度的方向与速度方向相同, 垂直于杆 ADAD, 大小满足

aDeτ=BDαAD=2rαAD a_D^{e\tau}=BD\alpha_{AD}=2r\alpha_{AD}

  • 法向加速度的方向指向旋转中点, 平行于杆 ADAD, 满足

aDen=BDωAD2=3v28r a_D^{en}=BD\omega_{AD}^2=\frac{3v^2}{8r}

同相对速度, 套筒仅会沿杆运动, 因此动点 DD 的相对加速度 aDr⃗\vec{a_D^r} 依然为沿杆 ADAD 方向

注意, 由于动系杆 ADAD 的角速度 ωAD≠0\omega_{AD}\neq 0, 因此还存在科氏加速度

aDk=2ωAD×vDr=3v24r a_D^k=2\omega_{AD}\times v_D^r=\frac{\sqrt{3}v^2}{4r}

其中科氏加速的方向需要具体分析. ωAD\omega_{AD} 为顺时针方向, 因此矢量方向为垂直纸面向下, 与 vDr⃗\vec{v_D^r} 通过右手定则得到 aDk⃗\vec{a_D^k} 方向

确定几个加速度分量的几何关系后画出动点 DD 的加速度简图

根据加速度合成定律

aD⃗=aDeτ⃗+aDen⃗+aDr⃗+aDk⃗ \vec{a_D}=\vec{a_D^{e\tau}}+\vec{a_D^{en}}+\vec{a_D^{r}}+\vec{a_D^{k}}

一个矢量方程能够分解为两个独立的方程, 解出两个未知量
对于此题, 仅未知量 αAD\alpha_{AD} 对于求出待求量有帮助, 因此仅求出 aDeτ⃗\vec{a_D^{e\tau}} 即可, 避免加速度分析中不必要的计算 (由于速度分析较简单, 且与加速度分析关联强, 因此能求出的未知量尽量求出)
为了最大程度避免额外未知量参与, 可沿待求未知量 aDeτ⃗\vec{a_D^{e\tau}} 方向分解矢量, 得到方程

aDeτ=−aDk=−3v24r a_D^{e\tau}=-a_D^k=-\frac{\sqrt{3}v^2}{4r}

根据其与 αAD\alpha_{AD} 的关系得出

αAD=−3v28r2 \alpha_{AD}=-\frac{\sqrt{3}v^2}{8r^2}

对动点 AA 进行加速度分析

由于杆 ADAD 绕铰链 BB 转动, 因此动点 AA 的绝对加速也由切向 aAτ⃗\vec{a_A^\tau} 与法向 aAn⃗\vec{a_A^n} 两部分组成, 满足

aAτ=ABαAD=−3v24r a_A^{\tau}=AB\alpha_{AD}=-\frac{\sqrt{3}v^2}{4r}

aAn=ABωAB2=3v28r a_A^{n}=AB\omega_{AB}^2=\frac{3v^2}{8r}

同样, 杆 AOAO 绕铰链 OO 转动, 动点的牵连加速度同样由两部分 aAeτ⃗\vec{a_A^{e\tau}} 与 aAen⃗\vec{a_A^{en}} 组成, 满足

aAeτ=AOαAO a_A^{e\tau}=AO\alpha_{AO}

aAen=AOωAO2=3v216r a_A^{en}=AO\omega_{AO}^2=\frac{3v^2}{16r}

并且动系 AOAO 存在角速度, 因此还有科氏加速度

aAk⃗=2ωAOvAr=33v28r \vec{a_A^{k}}=2\omega_{AO}v_A^r=\frac{3\sqrt{3}v^2}{8r}

整理几何关系可得动点 AA 的加速度简图为

根据加速度合成定律

aAτ⃗+aAn⃗=aAeτ⃗+aAen⃗+aAr⃗+aAk⃗ \vec{a_A^{\tau}}+\vec{a_A^{n}}=\vec{a_A^{e\tau}}+\vec{a_A^{en}}+\vec{a_A^{r}}+\vec{a_A^{k}}

加速度分量中, aAeτa_A^{e\tau} 与待求量 αAO\alpha_{AO} 有关, 因此沿 αAO⃗\vec{\alpha_{AO}} 方向分解 (注意等式两侧)

aAτcos⁡60∘+aAncos⁡30∘=aAeτ+aAk−3v28r+33v216r=aAeτ+338raAeτ=−53v216rαAO=−53v216r2 \begin{split}a_A^{\tau}\cos 60^\circ+a_A^{n}\cos 30^\circ&=a_A^{e\tau}+a_A^{k}\\ -\frac{\sqrt{3}v^2}{8r}+\frac{3\sqrt{3}v^2}{16r}&=a_A^{e\tau}+\frac{3\sqrt{3}}{8r}\\ a_A^{e\tau}&=-\frac{5\sqrt{3}v^2}{16r}\\ \alpha_{AO}&=-\frac{5\sqrt{3}v^2}{16r^2}\end{split}

解 αAO\alpha_{AO} 中的负号表明其实际方向与设定的正方向方向相反

最终得到题目的解

ωAO=3v4r,↻ \omega_{AO}=\frac{\sqrt{3}v}{4r},\circlearrowright

αAO=−53v216r2,↺ \alpha_{AO}=-\frac{5\sqrt{3}v^2}{16r^2},\circlearrowleft

刚体的平面运动

刚体转动

在刚体上选取任意基点, 刚体上其他点相对于基点的角速度与角加速度相同

基点法

将刚体上的点的运动分解为:

  • 相对于基点的转动 (刚体上两点距离不变, 只能做转动运动)
  • 基点作为动系的平动

选取基点 AA, 求刚体上的质点 BB 的运动有

基点法求速度

vB⃗=vA⃗+vBA⃗ \vec{v_B}=\vec{v_A}+\vec{v_{BA}}

其中

vBA⃗=ω⃗⋅AB⃗ \vec{v_{BA}}=\vec{\omega}\cdot\vec{AB}

基点法求加速度

aB⃗=aA⃗+aBAn⃗+aBAe⃗ \vec{a_B}=\vec{a_A}+\vec{a_{BA}^n}+\vec{a_{BA}^e}

其中

aBAn⃗=∣AB∣ω2=vBA2AB \vec{a_{BA}^n}=|AB|\omega^2=\frac{v_{BA}^2}{AB}

aBAt⃗=∣AB∣α \vec{a_{BA}^t}=|AB|\alpha

速度投影法

将基点法向 AB⃗\vec{AB} 投影可得, 对于刚体上任意两点, 满足

vA⃗⋅eAB⃗=vB⃗⋅eAB⃗ \vec{v_A}\cdot\vec{e_{AB}}=\vec{v_B}\cdot\vec{e_{AB}}

反映了刚体上任意两点距离不变的特性

速度瞬心法

  • 刚体上必定存在一点 CC, 满足 vC=0v_C=0
  • 通过对刚体上两点速度方向垂线的交线得到 CC
  • 如果垂线平行, 则能判断刚体平动, ω=0\omega=0
  • 对于刚体上任意一点 MM, vM=MC⋅ωv_M=MC\cdot\omega
  • 速度瞬心的加速度一般不为 00

加速度投影法

  • 当刚体平动 ω=0\omega=0 时使用
  • 此时没有法向加速度, 只有切向加速度, 表现出类似速度的性质
  • 因此有加速度投影法

aA⃗⋅eAB⃗=aB⃗⋅eAB⃗ \vec{a_A}\cdot\vec{e_{AB}}=\vec{a_B}\cdot\vec{e_{AB}}

加速度瞬心

  • 一般情况下加速度瞬心无法直接求得
  • 如果刚体 v≠0v\neq 0, 由于法向加速度, 加速度瞬心难以使用
  • 当 v=0v=0, 与速度瞬心性质类似, 加速度瞬心为两点加速度垂线的交点

纯滚动

  • 当圆柱体 (齿轮) 等于地面没有相对滑动, 则称为纯滚动
  • 设圆心 OO, 接触点 AA

纯滚动的运动特性

  • 当纯滚动的接触面为地面时 (静止物体, 圆心水平运动)
    • 纯滚动中, 接触点 vA=0v_A=0 为速度瞬心
    • 根据速度瞬心法可得

    vO=rω v_O=r\omega

    • 接触点不是加速度瞬心
    • 圆心的切向加速度满足

    aOt=rα a_O^t=r\alpha

  • 当纯滚动的接触面为弧面时, 圆心切向加速度不变, 还有法向加速度(注意与法向加速度公式区分)

aOn=vO2r+R=r2ω2r+R a_O^n=\frac{v_O^2}{r+R}=\frac{r^2\omega^2}{r+R}

  • 当相对于运动物块纯滚动时, 则以物块为动系, 当物块平动时, 满足

aOr=rα a_O^r=r\alpha

纯滚动的其他特性

  1. 对于绳子绕在圆柱上, 认为绳子与圆柱的接触点纯滚动
  2. 纯滚动的位置通常存在一个拉力 / 滑动摩擦力

齿轮问题

  • 齿轮齿数 zz 满足

z1z2=r1r2=i12 \frac{z_1}{z_2}=\frac{r_1}{r_2}=i_{12}

其中 i12i_{12} 为齿轮的传动比

  • 齿轮 / 齿条的啮合处 CC 为纯滚动, 且对于两齿轮速度相同, 满足

r1ω1=−r2ω2=vC r_1\omega_1=-r_2\omega_2=v_C

  • 注意外啮合的两个齿轮转向必定相反, 因此要加负号

刚体绕平行轴转动

对于二维动系中的刚体, 满足

ωa=ωr+ωe \omega_a=\omega_r+\omega_e

αa=αr+αe \alpha_a=\alpha_r+\alpha_e

曲柄固定齿轮问题

  • 对于曲柄固定齿轮的角速度问题, 可以设曲柄为动系, 其他齿轮相对曲柄运动, 此时齿轮圆心相对静止, 易于计算
  • 其中固定齿轮 ωa=ωr+ωe=0\omega_a=\omega_r+\omega_e=0
  • 由于要引入科氏加速度, 不适用于加速度计算

套筒问题

  1. 套筒内的刚体相对于套筒平动, 即刚体上各点的 vrv_r 相同, 刚体 ωr=0\omega_r=0
  2. 根据角速度叠加可得, 套筒内的刚体绝对角速度与绝对角加速度与套筒相同
  3. 与套筒转轴的重合点 PP 上, ve=0v_e=0, 因此 vr=vPv_r=v_P (套筒为动系, PP 为动点)

例题

半径为 rr 的圆盘 BB 在半径为 5r5r 的固定圆上纯滚动. 杆 OAOA 以匀角速度 3ω3\omega 转动, 求图示瞬间 ABAB 中点 CC 的速度和加速度以及圆盘 BB 的角速度和角加速度.

速度分析

统一采用逆时针方向为待求角速度与角加速度的方向

首先分析杆 ACAC

杆 ACAC 上的点 AA 绕点 OO 旋转, 此时速度 vA⃗\vec{v_A} 方向为水平向右. 杆 ACAC 上的点 BB 同时也是圆盘 BB 的圆心, 此时 BB 与固定圆圆心垂直于 OBOB, 因此速度 vB⃗\vec{v_B} 方向平行于 vA⃗\vec{v_A}. 杆 ABAB 上有两个平行的速度, 因此杆 ABAB 在此瞬间为平动, 有

vA=vB=vC=OAωAO=6rω v_A=v_B=v_C=OA\omega_{AO}=6r\omega

由于杆瞬时平动, 因此

ωAB=0 \omega_{AB}=0

分析圆盘 BB

圆盘与固定圆在接触点 DD 做纯滚动, 因此 BB 点的速度还满足

vB=rωB→ωB=6ω v_B=r\omega_B\to\omega_B=6\omega

加速度分析

点 AA 在匀速转动的杆 OAOA 上, 因此其加速度满足

aAτ=OAαOA=0 a_A^\tau=OA\alpha_{OA}=0

aAn=OAωOA2=18rω2 a_A^n=OA\omega_{OA}^2=18r\omega^2

点 BB 为纯滚动圆盘的圆心, 根据纯滚动的性质, BB 的加速度满足

aBτ=rαB a_B^\tau=r\alpha_{B}

aBn=r2ωB2r+5r=6rω2 a_B^n=\frac{r^2\omega_{B}^2}{r+5r}=6r\omega^2

以 AA 为基点对杆 ABAB 上的点 C,BC,B 分析

其中相对加速度满足

aACτ=ACαAB,  aACn=ACωAB2=0 a_{AC}^\tau=AC\alpha_{AB},\;a_{AC}^n=AC\omega_{AB}^2=0

aABτ=ABαAB,  aABn=ABωAB2=0 a_{AB}^\tau=AB\alpha_{AB},\;a_{AB}^n=AB\omega_{AB}^2=0

对于点 BB 有加速度合成方程

aBn⃗+aBτ⃗=aA⃗+aABn⃗+aABτ⃗(1) \vec{a_B^n}+\vec{a_B^\tau}=\vec{a_A}+\vec{a_{AB}^n}+\vec{a_{AB}^\tau}(1)

对于点 CC, 由于其绝对加速度 aC⃗\vec{a_C} 的大小与方向均无法确定, 因此将其沿杆 ABAB 分解为两个分量 aCx⃗\vec{a_{Cx}} 与 aCy⃗\vec{a_{Cy}}, 有

aCx⃗+aCy⃗=aA⃗+aACn⃗+aACτ⃗(2) \vec{a_{Cx}}+\vec{a_{Cy}}=\vec{a_A}+\vec{a_{AC}^n}+\vec{a_{AC}^\tau}(2)

对于方程 (1)(1) 中有两个未知量, 可以求解. 对于方程 (2)(2) 中有三个未知量, 可等方程 (1)(1) 求解完后再分析 (如果方程的未知量均大于 22, 则可先尝试往特定方向分解)

方程 (1)(1) 中未知的待求量为 aBτ(αB)a_{B}^\tau(\alpha_{B}) 与 aABτ(αAB)a_{AB}^\tau(\alpha_{AB}). 首先沿 ⊥aBτ⃗\perp \vec{a_{B}^\tau} 方向分解, 避开其中一个待求量有

aBn=aAn−aABnsin⁡30∘−aABτcos⁡30∘6rω2=18rω2−0−32aABτaABτ=83rω2αAB=23ω2 \begin{split}a_B^n &=a_A^n-a_{AB}^n\sin 30^\circ-a_{AB}^\tau\cos 30^\circ\\ 6r\omega^2 &=18r\omega^2-0-\frac{\sqrt{3}}{2}a_{AB}^\tau\\ a_{AB}^\tau &=8\sqrt{3}r\omega^2\\ \alpha_{AB} &=2\sqrt{3}\omega^2\end{split}

之后沿 aBτ⃗\vec{a_{B}^\tau} 方向分解, 求出另一个未知量

aBτ=aABncos⁡30∘−aABτcos⁡60∘aBτ=0−43rω2αB=−43ω2 \begin{split}a_{B}^\tau&=a_{AB}^n\cos 30^\circ-a_{AB}^\tau\cos 60^\circ\\ a_{B}^\tau&=0-4\sqrt{3}r\omega^2\\ \alpha_{B}&=-4\sqrt{3}\omega^2 \end{split}

方程 (1)(1) 中得出的 αAB\alpha_{AB} 即方程 (2)(2) 中的一个未知量, 因此此时方程 (2)(2) 可解

沿 aCx⃗\vec{a_{Cx}} 方向分解有

aCx=aACn−aAcos⁡60∘aCx=0−9rω2aCx=−9rω2 \begin{split}a_{Cx}&=a_{AC}^n-a_A\cos 60^\circ\\ a_{Cx}&=0-9r\omega^2\\ a_{Cx}&=-9r\omega^2\end{split}

沿 aCy⃗\vec{a_{Cy}} 方向分解有

aCy=aAcos⁡30∘−aACτaCy=93rω2−ACαABaCy=53rω2 \begin{split}a_{Cy}&=a_{A}\cos 30^\circ-a_{AC}^\tau\\ a_{Cy}&=9\sqrt{3}r\omega^2-AC\alpha_{AB}\\ a_{Cy}&=5\sqrt{3}r\omega^2\end{split}

综上可得

vC=6rω,方向向左 v_C=6r\omega,\text{方向向左}

aCx=9rω2,沿AB向下 a_{Cx}=9r\omega^2,\text{沿AB向下}

aCy=53rω2,垂直AB向下 a_{Cy}=5\sqrt{3}r\omega^2,\text{垂直AB向下}

ωB=6ω,逆时针方向 \omega_B=6\omega,\text{逆时针方向}

αB=43ω2,顺时针方向 \alpha_B=4\sqrt{3}\omega^2,\text{顺时针方向}