静力学

静力学基础

静力学公理

二力平衡

只受两个力的单个刚体 (任意形状) 处于平衡状态时, 两个力一定大小相同, 方向相反, 且在同一直线上

力的可传导性

单个刚体上的力可沿其作用线移动而不改变效果

三力交会平衡定理

受三个不平行的力的单个刚体处于平衡状态时, 三个力必定共面且交于一点

作用力与反作用力

相互作用的两个物体间总存在等值, 反向, 共线且分别作用于两个物体的一对力

刚化公理

平衡状态下, 可将变形体视为刚体 (平衡状态下, 可将柔绳等作为刚体)

力偶

• 两个等值, 平行, 反向的力组成的力系称为力偶
• 力偶间的最短距离 (垂直距离) 称为力偶臂 $d$
• 定义平面力偶矩 $M=\pm Fd$, 正负号取决于转动正方向
• 力偶矩与力偶的位置无关

约束

约束处存在约束力, 约束力大小未知, 根据主动力变化而变化

光滑接触面约束

约束力为接触点的公法线方向 (不一定是竖直方向)

铰链约束

• 铰链对两个连接体的约束力等值反向, 方向任意, 通常分解为 两个正交的未知力
• 当铰链上有两个以上物体时, 对各个物体的约束力之和为 $0$

固定铰链约束

与铰链约束相同, 由于地面通常静止, 因此铰链静止

活动铰链支座

约束力垂直于活动方向

插入端约束

插入端的各点收到多个力, 可等效为两个正交的约束力与一个约束力偶

受力分析

1. 未知力以正交分量的形式表现
2. 力的方向 (作用线) 确定, 大小未知时, 指向可以任意 (作为正方向)
3. 可用三力汇交提前确定部分力的方向
4. 先整体再部分, 分析部分注意反作用力
5. 整体受力图不需要表示内力

平面力系的简化

力平移定理

刚体内的力 $F$ 移动到任意一点 $B$ 后得到 $F'$, 为了不改变力的作用效果, 需要再补充一个附加力偶, 力偶矩大小 $M=M_{BF}$, 即原来的力 $F$ 对新点 $B$ 之矩

分布力系的化简

• 分布力系图示中的细实线 $ab$ 表现了分布力强度 $q(N/m)$ 随位置 $x(m)$ 的变化关系
• 根据积分可得, 等效合力的大小即图形面积
• 将分布力向分布力强度图的形心 $C$ 简化可不产生附加力矩
• 假设 $q_0=bB$

矩形分布力系

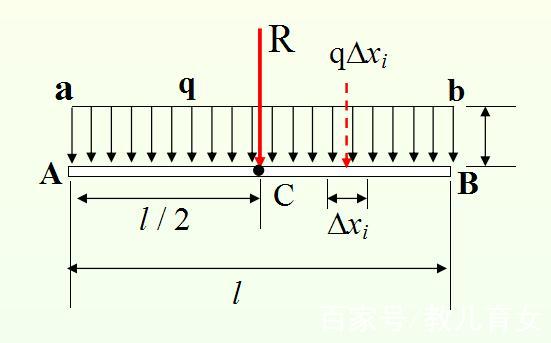
• 简化后等效合力为

$$R=q_0l$$

• 无附加力矩的简化点为

$$d=\frac{l}{2}$$

三角形分布力系

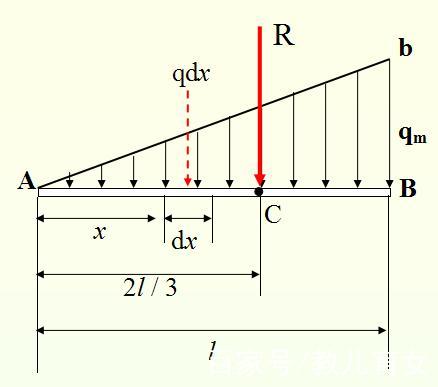
• 简化后等效合力为

$$R=\frac{q_0l}{2}$$

• 无附加力矩的简化点为

$$d=\frac{2}{3}l$$

平面力系的平衡条件

• 当平面力系平衡时, 将会满足

$$\vec{F_R}=\sum \vec{F}=0\\M_O=\sum M+\sum Fd=0$$

其中 $\vec{F_R}$ 为总和力, $M_O$ 为所有力对任意点之矩, 包括力偶矩

• 根据力系的化简可得, 一个平衡状态下的刚体可以提供 $3$ 个平衡方程
• 可通过指定方向 $F_x=0$ 与对任意点 $O$ 取矩得到三个平衡方程
• 三个方程中对两点 $A,B$ 取矩时, $AB$ 不能与 $F$ 分解方向垂直
• 三个方程对三点取矩时, 三点不能共线
• 对于二力杆, 取矩无意义, 仅有两个方程

平衡方程解题技巧

1. 可以将平衡状态下的组合体 (部分整体) 视为一个刚体使用平衡方程
2. 组合体中, 一个刚体可提供三个方程, 约束可提供等同于其约束反力数的方程, 无论从组合体还是刚体分析, 总方程数不变
3. 优先分析整体, 避免内力
4. 优先对多力交汇点取矩, 减小计算量
5. 优先向不求力的垂直方向分解, 减小计算量
6. 检查:
   1. 受力分析
   2. 方程是否少力, 少力矩
   3. 确认力矩方向

桁架分析

桁架构造

1. 所有杆件和受力均在同一平面内
2. 以三角形为结构基础
3. 支座反力量不超过 $3$ 个
4. 所有杆均为二力杆

内力计算

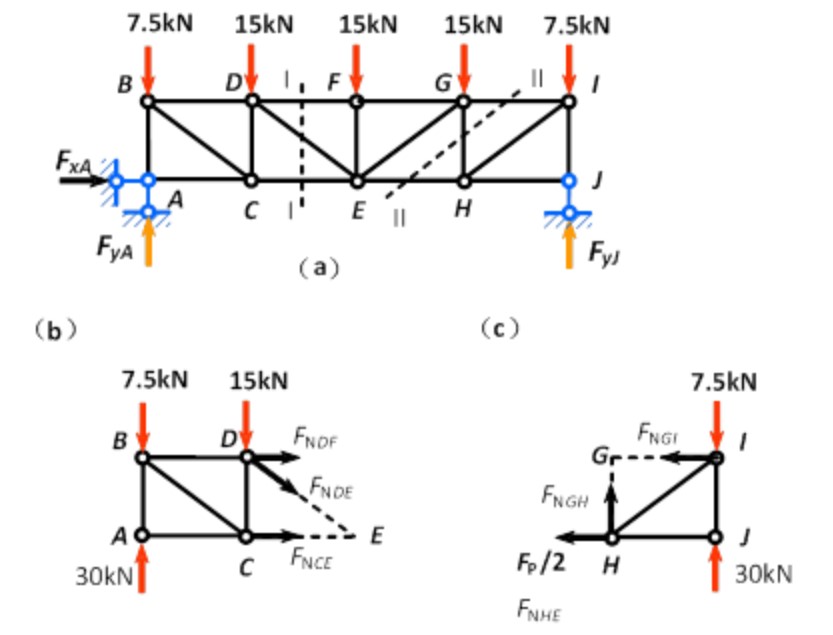
1. 以杆受拉方向为内力正方向 (因此节点所受的反力方向向外)
2. 沿指定方向截切桁架, 将得到部分视为刚体, 除原本所受外力外, 还受到沿被截切方向的, 来自被截切杆的内力 (拉力的反作用力, 方向与拉力相反)
3. 尽量一次仅截出三个未知量, 保证三个平衡方程可解

零力杆分析

由于均为二力杆, 因此外力必定在节点处 内力计算前, 可先移去零力杆, 简化计算

1. 一点两杆无外力
2. 一点两杆有外力, 外力沿其中一杆的方向, 则另一杆为零力杆
3. 一点三杆无外力, 其中两杆共线, 第三杆为零力杆

摩擦

滑动摩擦力

1. 作用在接触点, 沿接触点切线方向
2. 总是与运动趋势相反
3. 随主动力增大而增大, 满足

$$0\le F_s\le F_{max}=F_Nf_s$$

摩擦自锁

定义

$$\tan\varphi_f=f_s=\frac{F_{max}}{F_N}$$

当物体所受外力 $\vec{F_R}$ 与接触点的法线夹角 $\varphi<\varphi_f$ 时, $\vec{F_R}=\vec{F_N}+\vec{F_s}$, 物体总是保持平衡, 称为摩擦自锁

注意支持力 $F_N$ 的方向为法线方向, 即垂直于接触面

滚动摩擦力

• 实际情况下, 接触面为一个复杂的力系, 但可以分解为 $F_s,F_N,M_f$, 其中 $M_f$ 为滚阻力偶
• 滚阻力偶总是阻止物体滚动
• 随主矩增大而增大, 满足

$$0\le M_f\le M_{max}=F_N\delta$$

• 对于面接触中, 由于只能相对点翻滚, 因此在临界状态下, 可视为接触点为翻滚点的点接触 ($F_s,F_N$ 作用于此点)

摩擦平衡分析

在摩擦平衡分析中, 求临界力/质量时, 仅通过平衡方程一般无法求出所有力, 因此要假设部分摩擦处于临界状态作为已知条件

1. 先比较未知力 (包括未知摩擦力与摩擦滚阻) 与系统平衡方程数, 得到需要补充的临界条件数
2. 轮子逆时针滚动时, 质心向左移动, 存在顺时针的滚阻, 但可能不存在向左的滑动摩擦力 (没有相对滑动)
3. 轮子逆时针滚动时, 更可能出现向右滑动的趋势, 即打滑, 此时滑动摩擦力与滚阻的运动效果均与主矩相反, 更可能达到临界
4. 对于任何物体均存在滚动与滑动两种趋势, 且均有两个方向 (如果没有给出 $\delta$, 则不考虑滚动)
5. 由于 $\delta$ 一般较小, 因此滚动通常会是临界条件

空间力系分析

空间力矩论

对点之矩

• 对一固定点 $O$ 的力矩 $\vec{M_O}=\vec{r}\times\vec{F}$
• 其中 $r$ 为点 $O$ 到力作用点的矢量
• 与平面不同, 此时力矩为矢量

对轴之矩

对于空间的轴, 只有垂直于轴的分量有转动效果, 因此力矩为

$$M_{z}=\pm hF_{xy}$$

• $h$ 为力 $F$ 作用点到轴的距离
• 力对轴之矩等于力对轴上任一点之矩在轴上的投影 (用于计算任意轴的矩)

$$M_{l}=\vec{M_O}\frac{\vec{l}}{|l|}$$

空间力偶

• 定义空间力偶矢

$$\vec{M}=\vec{r}\times\vec{F}$$

• 其中 $\vec{r}$ 为力偶中两力作用点的矢量
• 空间力偶的具体指向可通过右手螺旋定则确定
• 空间力偶性质与平面力偶相同, 可以自由移动

空间力系的化简

空间力系的化简结果

对于任意空间力系可化简为 $\vec{F_R},\vec{M_O}$

1. $\vec{F_R}=0,\vec{M_O}=0$, 力系平衡
2. $\vec{F_R}\neq 0,\vec{M_O}=0$, 仅有一个力, 力系最简
3. $\vec{F_R}=0,\vec{M_O}\neq 0$, 无论向那点化简, 始终为一个力偶
4. $\vec{F_R}\neq 0,\vec{M_O}\neq 0$, 向其他点化简可以消去 $\vec{M_O}$, 得到 $\vec{F_R}\neq 0,\vec{M_O}=0$
5. $\vec{F_R}\parallel\vec{M_O}\neq 0$, 无法化简, 为一个力螺旋

空间力系的平衡条件

根据力系的化简可得, 一个平衡状态下的空间刚体可以提供 $6$ 个平衡方程

$$\sum F_x=0\;\sum F_y=0\;\sum F_z=0\\ \sum M_x=0\;\sum M_y=0\;\sum M_z=0$$

与平面类似, 可以对更多的轴取矩, 但不能对通过同一点的 $3$ 根以上的轴取矩, 也不能对 $3$ 根以上的平行轴取矩

• 选取轴时, 不一定是在已知杆上, 也可以是空间中的两点连线
• 选择与未知量共面的轴, 避开求未知量