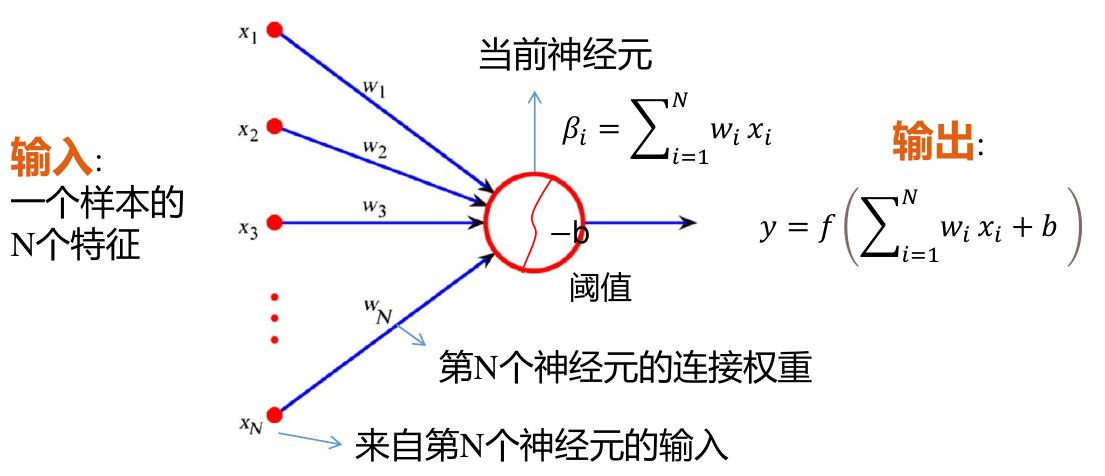
机器学习 MLP 分类器 单神经元基本结构 单个神经元具有如图所示的结构
神经元接收来自上一层网络所有单元的输出 通过权重向量 w ⃗ i \vec{w}_i w i x ⃗ \vec{x} x b i b_i b i f ( x ) f(x) f ( x ) 神经元的权重向量 w ⃗ i \vec{w}_i w i b i b_i b i 激活函数一般有 f ( x ) = sigmoid ( x ) = 1 1 + e − x f(x)=\operatorname{sigmoid}(x)=\frac{1}{1+e^{-x}} f ( x ) = sigmoid ( x ) = 1 + e − x 1 1 1 1 f ( x ) = ReLU ( x ) = max ( 0 , x ) f(x)=\operatorname{ReLU}(x)=\max(0,x) f ( x ) = ReLU ( x ) = max ( 0 , x ) 多隐藏层分类器 约定
分类器共有 m m m i i i k i k_i k i 对于第 i i i [ i ] [i] [ i ] 第 i i i p p p b p [ i ] b^{[i]}_{p} b p [ i ] b ⃗ [ i ] ∈ R k i × 1 \vec{b}^{[i]}\in \R^{k_i\times 1} b [ i ] ∈ R k i × 1 第 i i i p p p q q q w p , q [ i ] w^{[i]}_{p,q} w p , q [ i ] i i i p p p w ⃗ p [ i ] ∈ R 1 × k i − 1 \vec{w}^{[i]}_{p}\in\R^{1\times k_{i-1}} w p [ i ] ∈ R 1 × k i − 1 k i − 1 k_{i-1} k i − 1 i i i W [ i ] ∈ R k i × k i − 1 \bm{W}^{[i]}\in\R^{k_{i}\times k_{i-1}} W [ i ] ∈ R k i × k i − 1 k i k_i k i i i i f i ( z ⃗ [ i ] ) f_i(\vec{z}^{[i]}) f i ( z [ i ] ) 第 i i i 列向量 z ⃗ [ i ] ∈ R k i × 1 \vec{z}^{[i]}\in\R^{k_{i}\times 1} z [ i ] ∈ R k i × 1 z ⃗ [ i ] \vec{z}^{[i]} z [ i ] 行向量 a ⃗ [ i ] ∈ R 1 × k i \vec{a}^{[i]}\in\R^{1\times k_{i}} a [ i ] ∈ R 1 × k i 分类器的输出层使用 o o o W [ o ] , b ⃗ [ o ] \bm{W}^{[o]},\vec{b}^{[o]} W [ o ] , b [ o ] m + 1 m+1 m + 1 分类器的输入为样本在特征空间中的行向量 x ⃗ ∈ R 1 × k 0 \vec{x}\in\R^{1\times k_{0}} x ∈ R 1 × k 0 z ⃗ [ o ] = o ⃗ ∈ R k o × 1 \vec{z}^{[o]}=\vec{o}\in\R^{k_o\times 1} z [ o ] = o ∈ R k o × 1 多隐藏层分类器具有特点
由于各层单个神经元接收来自上一层的全部输入, 且不存在跨层链接, 因此称为 MLP 多隐藏层分类器, 或全连接网络, 前馈网络 当网络有至少一个隐藏层与足够的宽度, 能够逼近任何连续函数, 但需要大量参数, 并不现实 (万能近似定理) 正向传播过程 正向传播即各层的权重 W [ i ] \bm{W}^{[i]} W [ i ] b ⃗ [ i ] \vec{b}^{[i]} b [ i ] x ⃗ \vec{x} x o ⃗ \vec{o} o
对于第 i i i
{ z ⃗ [ i ] = W [ i ] a ⃗ [ i − 1 ] + b ⃗ [ i ] a ⃗ [ i ] = f i T ( z ⃗ [ i ] ) \begin{cases} \vec{z}^{[i]}=\bm{W}^{[i]}\vec{a}^{[i-1]}+\vec{b}^{[i]}\\ \vec{a}^{[i]}=f_i^T(\vec{z}^{[i]})\\ \end{cases} { z [ i ] = W [ i ] a [ i − 1 ] + b [ i ] a [ i ] = f i T ( z [ i ] )
其中
当 i = 1 i=1 i = 1 x ⃗ \vec{x} x a ⃗ [ 0 ] \vec{a}^{[0]} a [ 0 ] 取 f i T f_i^T f i T 对于输出层有
o ⃗ = a ⃗ [ o ] = f ′ ( W [ o ] a ⃗ [ m ] + b ⃗ [ o ] ) \vec{o}=\vec{a}^{[o]}=f'(\bm{W}^{[o]}\vec{a}^{[m]}+\vec{b}^{[o]}) o = a [ o ] = f ′ ( W [ o ] a [ m ] + b [ o ] )
反向传播过程 反向传播即已知训练集中各个样本的特征向量 x ⃗ i \vec{x}_i x i y ⃗ i \vec{y}_i y i W [ i ] \bm{W}^{[i]} W [ i ] b ⃗ [ i ] \vec{b}^{[i]} b [ i ]
首先定义损失函数 J ( y ⃗ , o ⃗ ) J(\vec{y},\vec{o}) J ( y , o ) y ⃗ \vec{y} y o ⃗ \vec{o} o
J ( y ⃗ , o ⃗ ) = 1 2 ( y ⃗ − o ⃗ ) 2 J(\vec{y},\vec{o})=\frac{1}{2}(\vec{y} - \vec{o})^2 J ( y , o ) = 2 1 ( y − o ) 2
当训练的模型符合要求时, 损失函数应为 J ( y ⃗ , o ⃗ ) = 0 J(\vec{y},\vec{o})=0 J ( y , o ) = 0 ∂ J ∂ w p , q [ i ] \frac{\partial J}{\partial w^{[i]}_{p,q}} ∂ w p , q [ i ] ∂ J
{ w p , q [ i ] ′ = w p , q [ i ] − α ∂ J ∂ w p , q [ i ] b p [ i ] ′ = b p [ i ] − α ∂ J ∂ b p [ i ] \begin{cases} w^{[i]'}_{p,q}=w^{[i]}_{p,q}-\alpha\frac{\partial J}{\partial w^{[i]}_{p,q}}\\ b^{[i]'}_{p}=b^{[i]}_{p}-\alpha\frac{\partial J}{\partial b^{[i]}_{p}} \end{cases} ⎩ ⎨ ⎧ w p , q [ i ] ′ = w p , q [ i ] − α ∂ w p , q [ i ] ∂ J b p [ i ] ′ = b p [ i ] − α ∂ b p [ i ] ∂ J
其中 α \alpha α α ∈ [ 0 , 1 ] \alpha\in[0,1] α ∈ [ 0 , 1 ]
对于偏导数 w p , q [ i ] ′ w^{[i]'}_{p,q} w p , q [ i ] ′ 矢量求导法则 得到, 具体见附录
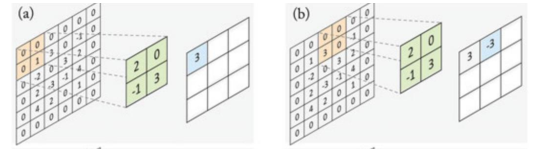
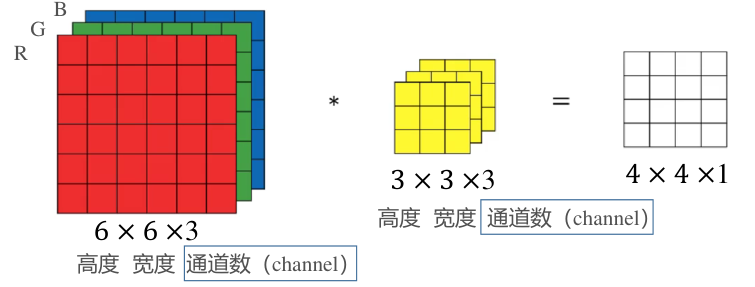
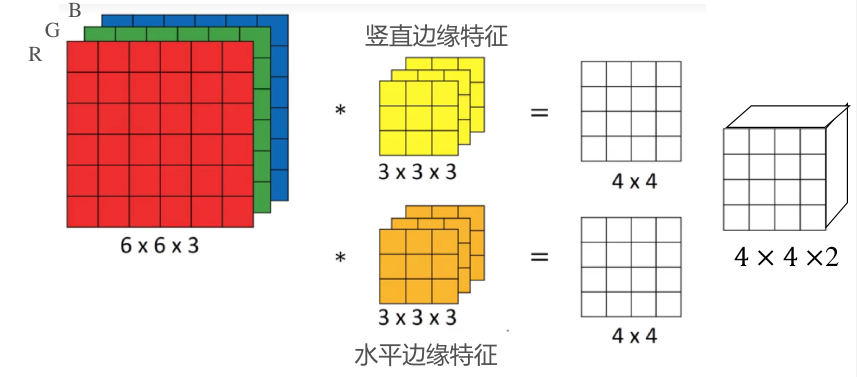
CNN 卷积神经网络 广义卷积运算 边缘填充 通常卷积时, 图像边界的信息参与运算的次数远小于中心参与卷积运算的次数, 导致边缘信息得不到有效利用 为此可在图像的边缘填充 0 0 0 使用参数 p p p p p p 对于传统卷积, p = 0 p=0 p = 0 具有步长的卷积 通常卷积核在遍历扫描时每次只移动一个像素 通过指定步长参数 s s s s s s 对于传统卷积, s = 1 s=1 s = 1 多通道卷积 对于多通道的输入图像, 卷积核也将具有与输入图像相同的通道数 卷积核依然沿平面运动, 且每次移动得到一个卷积结果 卷积运算时, 将根据卷积核所在位置, 计算出图像各通道的各点与卷积对应通道对应点的乘积和作为卷积结果 卷积输入与输出图像的关系 对于 ( W × H × C ) (W\times H\times C) ( W × H × C ) f × f × C f\times f\times C f × f × C p , s p, s p , s
[ W − f + 2 p s ] + 1 × [ H − f + 2 p s ] + 1 × 1 \Bigg[\frac{W-f+2p}{s}\Bigg]+1\times \Bigg[\frac{H-f+2p}{s}\Bigg]+1\times 1 [ s W − f + 2 p ] + 1 × [ s H − f + 2 p ] + 1 × 1
其中 [ x ] [x] [ x ]
CNN 中的网络层 卷积层 可以将卷积视为一种特殊的神经网络, 输出图像的每个像素视为一个节点 卷积核内的参数即神经网络的权重参数, 通过卷积核计算节点对应输入图像的一块像素区, 因此卷积层与一般全连接神经网络不同 卷积层的一个节点仅连接上一层部分输入 所有节点共用一个权重与偏置, 可以显著减小网络的参数数 一个卷积层可能还具有多个相同的卷积核, 卷积层的输出图像通道数即该卷积层的卷积核数量, 且每个卷积核还具有一个偏置 卷积层并不具有激活函数, 还需要人为添加激活函数层, 一般为 ReLu 池化层 也称为降采样层
池化层为一种特殊的卷积层, 通常用于提取卷积结果中的有效信息并传入下一层 池化层的卷积核大小 f f f s s s p p p 池化层卷积以卷积核中所有输入的最大值作为输出 (最大值池化), 也有以输入的平均值作为输出 (均值池化) 全连接层 对于输入图像经过多次卷积后, 一般会再拉伸为一维的特征向量, 并作为之后的全连接层输入
CNN 的训练 梯度下降参数 Batch 一批数据 Iteration 一次训练 Epoch 一代训练 梯度下降方法 BGD 批量梯度下降 Mini-Batch 小批量梯度下降 SGD 随机梯度下降 正则化 如果模型参数太多, 训练样本又太少, 很容易产生过拟合
数据正则化 Batch Normalization 随机断开连接 Dropout 附录: MLP 反向传播的推导 以下以第 m m m
∂ J ∂ w p , q [ m ] = ∂ J ∂ o ⃗ ⋅ ∂ o ⃗ ∂ z ⃗ [ o ] ⋅ ∂ z ⃗ [ o ] ∂ a ⃗ [ m ] ⋅ ∂ a ⃗ [ m ] ∂ z ⃗ [ m ] ⋅ ∂ z ⃗ [ m ] ∂ w p , q [ m ] \frac{\partial J}{\partial w^{[m]}_{p,q}}=\frac{\partial J}{\partial \vec{o}}\cdot\frac{\partial \vec{o}}{\partial \vec{z}^{[o]}}\cdot\frac{\partial \vec{z}^{[o]}}{\partial \vec{a}^{[m]}}\cdot\frac{\partial \vec{a}^{[m]}}{\partial \vec{z}^{[m]}}\cdot\frac{\partial \vec{z}^{[m]}}{\partial w^{[m]}_{p,q}} ∂ w p , q [ m ] ∂ J = ∂ o ∂ J ⋅ ∂ z [ o ] ∂ o ⋅ ∂ a [ m ] ∂ z [ o ] ⋅ ∂ z [ m ] ∂ a [ m ] ⋅ ∂ w p , q [ m ] ∂ z [ m ]
根据矢量求导法则 可得出各个部分的导数满足
{ ∂ J ∂ o ⃗ = ( o ⃗ − y ⃗ ) ∈ R 1 × k o ∂ o ⃗ ∂ z ⃗ [ o ] = diag [ f o ′ ( z ⃗ [ o ] ) ] ∈ R k o × k o ∂ z ⃗ [ o ] ∂ a ⃗ [ m ] = W [ o ] ∈ R k o × k m ∂ a ⃗ [ m ] ∂ z ⃗ [ m ] = diag [ f m ′ ( z ⃗ [ m ] ) ] ∈ R k m × k m ∂ z ⃗ [ m ] ∂ w p , q [ m ] = [ 0 … a q [ m − 1 ] … 0 ] T ∈ R k m × 1 \begin{cases} \frac{\partial J}{\partial \vec{o}}=(\vec{o}-\vec{y})\in\R^{1\times k_o}\\ \frac{\partial \vec{o}}{\partial \vec{z}^{[o]}}=\operatorname{diag}[f'_o(\vec{z}^{[o]})]\in\R^{k_o\times k_o}\\ \frac{\partial \vec{z}^{[o]}}{\partial \vec{a}^{[m]}}=\bm{W}^{[o]}\in\R^{k_o\times k_m}\\ \frac{\partial \vec{a}^{[m]}}{\partial \vec{z}^{[m]}}= \operatorname{diag}[f'_m(\vec{z}^{[m]})]\in\R^{k_m\times k_m}\\ \frac{\partial \vec{z}^{[m]}}{\partial w^{[m]}_{p,q}}=\begin{bmatrix}0&\dots&a^{[m-1]}_q&\dots&0\end{bmatrix}^T\in\R^{k_{m}\times 1} \end{cases} ⎩ ⎨ ⎧ ∂ o ∂ J = ( o − y ) ∈ R 1 × k o ∂ z [ o ] ∂ o = diag [ f o ′ ( z [ o ] )] ∈ R k o × k o ∂ a [ m ] ∂ z [ o ] = W [ o ] ∈ R k o × k m ∂ z [ m ] ∂ a [ m ] = diag [ f m ′ ( z [ m ] )] ∈ R k m × k m ∂ w p , q [ m ] ∂ z [ m ] = [ 0 … a q [ m − 1 ] … 0 ] T ∈ R k m × 1
其中
参数 W , b ⃗ \bm{W},\vec{b} W , b a q [ m − 1 ] a^{[m-1]}_q a q [ m − 1 ] 矢量 [ 0 … a q [ m − 1 ] … 0 ] T \begin{bmatrix}0&\dots&a^{[m-1]}_q&\dots&0\end{bmatrix}^T [ 0 … a q [ m − 1 ] … 0 ] T a q [ m − 1 ] a^{[m-1]}_q a q [ m − 1 ] p p p 初始条件下, 通常令参数 W , b ⃗ \bm{W},\vec{b} W , b 推广可得, 对于第 i i i ∂ w p , q [ m ] \partial w^{[m]}_{p,q} ∂ w p , q [ m ] m + 1 m+1 m + 1
∂ J ∂ w p , q [ i ] = ( o ⃗ − y ⃗ ) ( ∏ j = m + 1 i + 1 diag [ f j ′ ( z ⃗ [ j ] ) ] W [ j ] ) [ 0 ⋮ f i ′ ( z p [ i ] ) a q [ m − 1 ] ⋮ 0 ] \frac{\partial J}{\partial w^{[i]}_{p,q}}=(\vec{o}-\vec{y})\bigg(\prod_{j=m+1}^{i+1}\operatorname{diag}[f'_j(\vec{z}^{[j]})]\bm{W}^{[j]}\bigg)\begin{bmatrix}0\\ \vdots\\ f'_i(z^{[i]}_p)a^{[m-1]}_q\\ \vdots\\ 0\end{bmatrix} ∂ w p , q [ i ] ∂ J = ( o − y ) ( j = m + 1 ∏ i + 1 diag [ f j ′ ( z [ j ] )] W [ j ] ) 0 ⋮ f i ′ ( z p [ i ] ) a q [ m − 1 ] ⋮ 0
根据以上公式, 定义梯度行矢量 δ ⃗ [ i ] ∈ R 1 × k i \vec{\delta}^{[i]}\in\R^{1\times k_i} δ [ i ] ∈ R 1 × k i
δ ⃗ [ i ] = ( o ⃗ − y ⃗ ) ( ∏ j = m i + 1 diag [ f j ′ ( z ⃗ [ j ] ) ] W [ j ] ) = { δ ⃗ [ i + 1 ] diag [ f i + 1 ′ ( z ⃗ [ i + 1 ] ) ] W [ i + 1 ] , i < m ( o ⃗ − y ⃗ ) , i = m + 1 \begin{split} \vec{\delta}^{[i]}&=(\vec{o}-\vec{y})\bigg(\prod_{j=m}^{i+1}\operatorname{diag}[f'_j(\vec{z}^{[j]})]\bm{W}^{[j]}\bigg)\\ &= \begin{cases} \vec{\delta}^{[i+1]}\operatorname{diag}[f'_{i+1}(\vec{z}^{[i+1]})]\bm{W}^{[i+1]}&,i<m\\ (\vec{o}-\vec{y})&,i=m+1 \end{cases} \end{split} δ [ i ] = ( o − y ) ( j = m ∏ i + 1 diag [ f j ′ ( z [ j ] )] W [ j ] ) = { δ [ i + 1 ] diag [ f i + 1 ′ ( z [ i + 1 ] )] W [ i + 1 ] ( o − y ) , i < m , i = m + 1
此时系数 W , b ⃗ \bm{W},\vec{b} W , b
{ ∂ J ∂ w p , q [ i ] = δ p [ i ] f i ′ ( z p [ i ] ) a q [ m − 1 ] ∂ J ∂ b p [ i ] = δ p [ i ] f i ′ ( z p [ i ] ) → { w p , q [ i ] ′ = w p , q [ i ] − α δ p [ i ] f i ′ ( z p [ i ] ) a q [ m − 1 ] W [ i ] ′ = W [ i ] − α [ a ⃗ [ m − 1 ] ( δ ⃗ [ i ] diag [ f j ′ ( z ⃗ [ j ] ) ] ) ] T b p [ i ] ′ = b p [ i ] − α δ p [ i ] f i ′ ( z p [ i ] ) \begin{cases} \frac{\partial J}{\partial w^{[i]}_{p,q}}=\delta^{[i]}_pf'_i(z^{[i]}_p)a^{[m-1]}_q\\ \frac{\partial J}{\partial b^{[i]}_{p}}=\delta^{[i]}_pf'_i(z^{[i]}_p) \end{cases}\to \begin{cases} w^{[i]'}_{p,q}=w^{[i]}_{p,q}-\alpha\delta^{[i]}_pf'_i(z^{[i]}_p)a^{[m-1]}_q\\ \bm{W}^{[i]'}=\bm{W}^{[i]}-\alpha\Big[\vec{a}^{[m-1]}\big(\vec{\delta}^{[i]}\operatorname{diag}[f'_j(\vec{z}^{[j]})]\big)\Big]^T\\ b^{[i]'}_{p}=b^{[i]}_{p}-\alpha\delta^{[i]}_pf'_i(z^{[i]}_p) \end{cases} ⎩ ⎨ ⎧ ∂ w p , q [ i ] ∂ J = δ p [ i ] f i ′ ( z p [ i ] ) a q [ m − 1 ] ∂ b p [ i ] ∂ J = δ p [ i ] f i ′ ( z p [ i ] ) → ⎩ ⎨ ⎧ w p , q [ i ] ′ = w p , q [ i ] − α δ p [ i ] f i ′ ( z p [ i ] ) a q [ m − 1 ] W [ i ] ′ = W [ i ] − α [ a [ m − 1 ] ( δ [ i ] diag [ f j ′ ( z [ j ] )] ) ] T b p [ i ] ′ = b p [ i ] − α δ p [ i ] f i ′ ( z p [ i ] )