跳至主要內容

中级视觉

大约 8 分钟

中级视觉

Harris 角点检测

角点检测原理

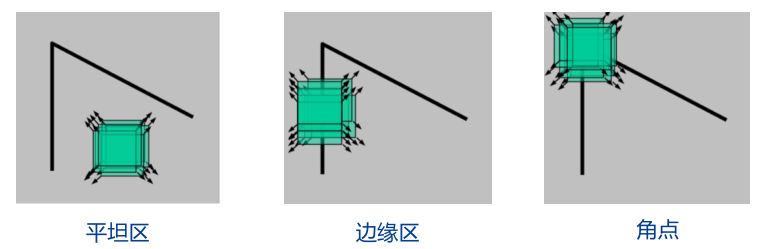
在数学上定义角点时, 规定一个以点 PP 为中心的窗口 WW, 当窗口沿任意方向移动时, 窗口内的灰度均发生了明显变化, 则认为点 PP 为一个角点

  • 当窗口沿任意方向移动灰度变化小, 则为平坦区
  • 当窗口沿特定方向移动灰度变化大, 垂直方向变化小, 则为边缘区
  • 当窗口沿任意方向移动灰度变化大, 则为角点

衡量窗口灰度变化时使用如下误差函数

E(u,v)=∑(x,y)∈Wω(x,y)[F(x+u,y+v)−F(x,y)]2 E(u,v)=\sum_{(x,y)\in W}\omega(x,y)[F(x+u,y+v)-F(x,y)]^2

其中

  • u,vu,v 为窗口的移动距离
  • F(x,y)F(x,y) 为原始图像上点 x,yx,y 的像素值
  • ω(x,y)\omega(x,y) 为加权函数, 通常即高斯滤波卷积核
  • 公式即使用窗口移动前后对应点误差的平方和衡量灰度变化

区域特征值与特征向量

根据泰勒展开

F(x+u,y+v)≈F(x,y)+u∂F∂x∣x,y+v∂F∂y∣x,y F(x+u,y+v)\approx F(x,y)+u\frac{\partial F}{\partial x}\big|_{x,y}+v\frac{\partial F}{\partial y}\big|_{x,y}

使用 Sobel 算子得到的图像梯度代替其中的导数, 可得此时对应点 (x,y)(x,y) 的误差的平方和满足 (注意其中的矩阵不是二阶偏导矩阵)

[F(x+u,y+v)−F(x,y)]2≈[[GxGy](x,y)[uv]]2≈[uv][Gx2GxGyGxGyGy2](x,y)[uv] \begin{split} [F(x+u,y+v)-F(x,y)]^2&\approx \Bigg[\begin{bmatrix}G_x&G_y\end{bmatrix}_{(x,y)}\begin{bmatrix}u\\ v\end{bmatrix}\Bigg]^2\\ &\approx \begin{bmatrix}u& v\end{bmatrix} \begin{bmatrix} G_x^2& G_xG_y\\ G_xG_y& G_y^2 \end{bmatrix}_{(x,y)} \begin{bmatrix}u\\ v\end{bmatrix} \end{split}

通过泰勒展开可排除 E(u,v)E(u,v) 中移动位置的影响 ([uv]\begin{bmatrix}u& v\end{bmatrix} 可视为常数提出), 定义自相关系数矩阵 M\bm{M} 满足 (注意 M\bm{M} 为窗口中一系列梯度矩阵的加权和)

M=∑(x,y)∈Wω(x,y)[Gx2GxGyGxGyGy2](x,y) \bm{M}=\sum_{(x,y)\in W}\omega(x,y)\begin{bmatrix} G_x^2& G_xG_y\\ G_xG_y& G_y^2 \end{bmatrix}_{(x,y)}

将自相关系数矩阵相似对角化后, 此时的误差函数满足

E(u,v)≈[uv]M[uv]≈[uv]Q[λ1λ2]QT[uv] \begin{split} E(u,v)&\approx\begin{bmatrix}u& v\end{bmatrix}\bm{M}\begin{bmatrix}u\\ v\end{bmatrix}\\ &\approx \begin{bmatrix}u& v\end{bmatrix}\bm{Q}\begin{bmatrix}\lambda_1&\\&\lambda_2\end{bmatrix}\bm{Q}^{T}\begin{bmatrix}u\\ v\end{bmatrix} \end{split}

因此像素点 P(x,y)P(x,y) 的误差函数 E(u,v)E(u,v) 可以近似为一个二次型, 二次型的特征值 λ1,λ2\lambda_1,\lambda_2 反映了窗口随不同方向移动时误差变化的最快与最慢方向, 由角点的数学定义可知

  • 当 λ1,λ2\lambda_1,\lambda_2 均很小时, 为平坦区
  • 当 λ1\lambda_1 很大, λ2\lambda_2 很小时, 为边缘区
  • 当 λ1,λ2\lambda_1,\lambda_2 均很大时, 为角点

角点响应函数

在实际使用时, 在得到自相关系数矩阵 M\bm{M} 一般通过以下角点响应函数 RR 判断其是否满足角点的特点, 函数值越大表明约有可能是角点

  • R(M)=det⁡(M)−αtr⁡2(M)=λ1λ2−α(λ1+λ2)2,α≈0.06R(\bm{M})=\det(\bm{M})-\alpha\operatorname{tr}^2(\bm{M})=\lambda_1\lambda_2-\alpha(\lambda_1+\lambda_2)^2,\alpha\approx 0.06
  • R(M)=λ1−αλ2,α≈0.05R(\bm{M})=\lambda_1-\alpha\lambda_2,\alpha\approx 0.05

取大于阈值部分的局部最大值点作为检测到的角点

Canny 边缘检测

边缘检测准备

在进行边缘检测前, 首先需要用高斯滤波去除图像的噪声

之后还需要使用 Sobel 算子计算出图像各点沿 x,yx,y 方向的差分 Gx,GyG_x,G_y
通过两个方向的差分可以计算出图像的图像的梯度大小 SS 及方向 θ\theta 满足

{S=Gx2+Gy2θ=Arctan⁡(Gy,Gx) \begin{cases} S=&\sqrt{G_x^2+G_y^2}\\ \theta=&\operatorname{Arctan}(G_y,G_x) \end{cases}

非极大值抑制

根据导数的特点, 当函数在点 PP 上有最大的变化率时, 其一阶导数必定在 PP 处有极值
非极大值抑制正是基于这一原理筛选出可能的边缘点

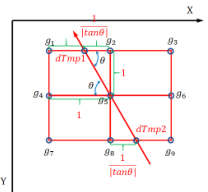
对于像素点 PP 的梯度方向 θ\theta, 使用如图所示的方法, 通过 PP 八邻域内的像素点插值得到 PP 梯度方向上前后两点的梯度大小
然后比较 PP 与其前后两点的梯度大小, 当 PP 的梯度 SS 大于前后两点则作为可能的边缘点保留

双阈值滤波

对于非极大值抑制中得到的边缘点进行滤波

  • 对于阈值下界 T1T_1 与上界 T2T_2
  • 梯度大于上界的必定为边缘点
  • 小于下界的必定不是边缘点
  • 在上下界中, 与边缘点相连的点也视为边缘点

纹理分析

纹理一般表述为图像强度局部变化的重复模式, 是图像粗糙性, 光滑性, 规则性等度量

灰度共生矩阵分析

灰度共生矩阵中的元素, 表示的是具有某种空间位置关系的两个像素灰度的联合分布
对于 8 位灰度图片的一个方向, 灰度共生矩阵为 R256×256\R^{256\times 256} 的矩阵

  • 首先定义扫描方向 (a,b)(a,b), 通常共有 0,45,90,135∘0,45,90,135^\circ 四个扫描方向
    如 a=1,b=0a=1,b=0 表示沿 0∘0^\circ 方向扫描; a=−1,b=1a=-1,b=1 表示沿 135∘135^\circ 方向扫描
  • 扫描点 (x,y)(x,y) 与扫描方向下的点 (x+a,y+b)(x+a,y+b) 的灰度组成灰度对 (f1,f2)(f_1,f_2)
  • 使用 R256×256\R^{256\times 256} 的灰度共生矩阵, 矩阵中 (i,j)(i,j) 元素表示了灰度对 (f1,f2)(f_1,f_2) 出现的概率 (频次除以总对数)
  • 通过对灰度共生矩阵的以下统计, 确定纹理特性
    • 角二阶矩 纹理细度
    • 熵 纹理随机性
    • 对比度 局部变化
    • 反差分矩阵 纹理规则程度

傅里叶频谱分析

通过观察纹理图片的中心化傅里叶频谱图可用于分析纹理的特性

  • 对于纹理较粗的图像, 能量集中在离原点较近的范围内, 这些点有较大的幅值, 细纹理相反
  • 对于条纹纹理, 使用阈值二值化的频谱图在垂直于图像纹理方向上, 将体现为一条直线带

局部二值分析

对于点 PP 的局部二值为

  • 取出点 PP 半径为 RR 的圆形领域中的点
  • 分别比较圆周点与中心点 PP 的灰度, 并由比较结果组成一个二进制序列作为局部二值结果
  • 具有对比度与旋转不变性

自相关函数

  • 求出图像自身对自身的卷积, 得到自相关函数
  • 粗纹理自相关函数随距离增大下降速度较慢, 细纹理相反
  • 如果纹理基元中灰度呈周期变化, 则自相关函数的升降也呈周期性变化

图像变形

图像变换矩阵

  • 使用二维齐次变换矩阵 T\bm{T} 描述平移, 旋转, 缩放, 错切等基础变换
    输入图片 FF 与变换后的图片 F′F' 之间满足 F(p⃗)=F′(Tp⃗)F(\vec{p})=F'(\bm{T}\vec{p})
  • 图像变换时一般有以下使用 Inverse Warping 策略
    • 遍历变换后的图片 F′(p⃗)F'(\vec{p}) 中的每一个像素点 (注意 p⃗\vec{p} 的元素值为离散的)
    • 对于点 p⃗\vec{p} 在变换后图片的像素值有 F′(p⃗)=F(T−1p⃗)F'(\vec{p})=F(\bm{T}^{-1}\vec{p})
    • 由于 FF 中的已知点的坐标均为离散的整数, 但 T−1p⃗\bm{T}^{-1}\vec{p} 可能是小数, 因此需要插值

最近邻插值

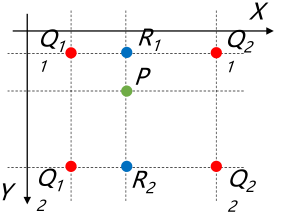
  • 当 p⃗\vec{p} 坐标为小数时, 其必定落在网格的中间
  • 对于一个网格的四个角点分别为四个灰度已知的原图像素点 Q11,…,Q22Q_{11},\dots,Q_{22}
  • 以四个角点中, 离点 p⃗\vec{p} 最近的像素点的像素值作为插值结果
  • 插值计算量小, 但马赛克效应较强

双线性插值

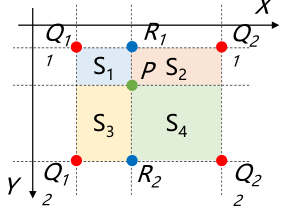
  • 同上, p⃗\vec{p} 将落在网格中, 且有四个邻近的已知像素点
  • 通过做 p⃗\vec{p} 的水平与垂直分线, 将网格划分为四个小块
    角点对角位置的小块面积体现了其对于点 p⃗\vec{p} 取值的贡献
  • 因此 p⃗\vec{p} 的插值结果满足
    F(p⃗)=S4⋅F(Q11)+S3⋅F(Q21)+S2⋅F(Q12)+S1⋅F(Q22)F(\vec{p})=S_4\cdot F(Q_{11})+S_3\cdot F(Q_{21})+S_2\cdot F(Q_{12})+S_1\cdot F(Q_{22})
  • 插值计算量大, 但马赛克效应较小

霍夫变换

在霍夫变换前, 通常需要先使用 Canny 算子提取出二值化的边缘点, 再对二值化的点进行进一步处理

霍夫直线变换

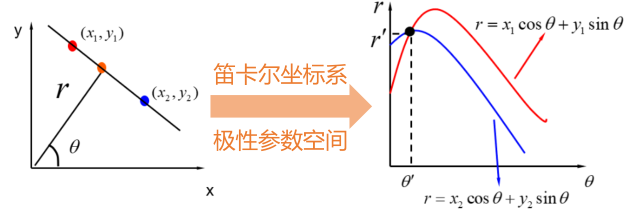
对于方程 r=xcos⁡θ+ysin⁡θr=x\cos\theta+y\sin\theta

  • 如果 r,θr,\theta 确定, 则该方程可以表示为一条直线
    参数 rr 反映了直线到原点的距离, 参数 θ\theta 表示原点到垂足的方向角
  • 如果 x,yx,y 确定, 则该方程可以表示为一条正弦曲线
    正弦曲线上的每一个点 (r,θ)(r,\theta) 都可以作为一条过点 (x,y)(x,y) 的直线的参数

根据以上原理可以得到如下直线检测算法

  1. 确定距离 rr 与角度 θ\theta 的分辨率以及范围, 根据分辨率与范围得出统计刻度以及对应的统计表
  2. 遍历边缘点, 对每个被遍历点 (x,y)(x,y) 得到对应的正弦曲线, 并计算各个 θ\theta 刻度下对应的 rr
  3. 对于每个计算得到的 (θ,r)(\theta,r) 都使统计表定义位置的计数加一
  4. 将统计表称为图像的霍夫直线变换, 以其中大于给定阈值的点 (r^,θ^)(\hat{r},\hat{\theta}) 作为匹配到的直线结果

霍夫圆变换

略