正弦稳态与三相电路分析
正弦稳态电路
相量法
正弦电量
u=Umcos(ωt+ϕ)
- u 瞬时值
- Um 最大值
- ω 角频率
- ϕ 初相位
- U=2Um 有效值(电表测量结果)
相量法
U˙=U∠ϕ
- 相量中实部使用的是有效值, 转成瞬时值需要化为最大值
- 使用相量的实部体现瞬时值
- 基尔霍夫定律依然满足, 但需要使用相量计算
相量分析法
- 通过画图, 结合相量之间的几何关系解题
- 分析前选择一个相量为参考, 令其相位角为 0∘
- 参考向量选择
- 电路已知条件最多的部分
- 在电路最内部
- 电阻上的 I˙(串) 或 U˙(并)
阻抗
元件阻抗
电阻
Z=R
电感
Z=jωL
电容
Z=jωC1
阻抗性质
U˙=I˙Z
- 阻抗依然满足串联与并联
- 感性阻抗 ϕ>0, U˙ 超前
- 容性阻抗 ϕ<0, U˙ 滞后
- 由 1 得阻抗角度也体现 U˙ 与 I˙ 的夹角
功率
- 功率计算所用到的均为有效值
- 由功率求得 U, I 后还需转化为相量
- 公式中均使用参考方向
- 除视在功率均满足功率守恒
有功功率
P=UIcos(ϕU−ϕI)
单位 W
无功功率
Q=UIsin(ϕU−ϕI)
单位 var
复功率
Sˉ=P+jQ=ZI2=U˙I˙
单位为 V⋅A
元件复功率相位角即阻抗相位角
视在功率
S=UI
单位为 V⋅A
S=P2+Q2
视在功率不满足功率守恒
功率因数
λ=SP=cos(ϕU−ϕI)
功率因数即阻抗角的余弦值
阻抗角可能取正或负, 通过成感性(正)/容性(负)确定
功率因数矫正
- 前提: 不改变负载的工作状态(电压)
- 通过并联电容, 提高端口的功率因数
- 分析时令 U˙ 的相位为 0, 则 I˙ 的相位为 −ϕ
- 向 y 轴方向投影 I˙, 比较其与目标功率因数下投影大小的差值(仅增加电容, x 方向投影不会改变)
- 由于并联分流, 因此此差值即矫正电容分压大小(端口电压不变)
最大功率传输
- 当负载阻抗与网络戴维南支路的等效阻抗满足共轭关系时, 负载获得的功率最大
ZL=Zeq
PLmax=4ReqUoc2
其中 Uoc 为等效电路的电压源有效值, Req 为等效阻抗的实部
RL=∣Zeq∣
易错知识点
- 阻抗 X 一定大于零, Z 相位角一定在 −90∘<θ<90∘ 范围内
- 结合 1, 当仅电量的模长已知时, 可通过 KCL/KVL 结合相量图, 提前求出电量的方向
- 相量的模长为有效值, 直接使用其 x 方向投影无意义
三相电路
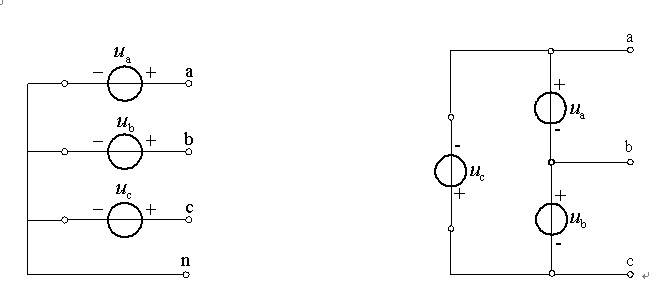
- 对称三相电压中, 满足 U˙A+U˙B+U˙C=0
- U˙A,U˙B,U˙C 按顺时针顺序以 120∘ 夹角排列
- 相电压 Uxp 仅含 x 与中性点 N 的电压, 因此也可写成 UAN
- 线电压 Uxl x 与 y(下一相) 对应节点之间的电压, 因此也可写成 UAB
- 相电流 Ixp 线电流在 Uxl x 与 y(下一相) 的 x 分流电流中
- 线电流 Ixl x 端口上的总电流
星形联结(Y形)
U˙xl=3U˙xp∠30∘
三角形联结(Δ形)
I˙xl=3I˙xp∠−30∘
- 三角形联结中, 电压源正负极首尾相接, 按顺时针顺序排列
分相计算
此处公式仅适用于对称电路, 此时三相的电流电压关系完全相同, 负载大小相同
Y-Y
- 取出其中一相与中性点构成回路, 计算此回路中的电量
- 无论中性点上电阻取何值(短路或开路), 中性点上电流为 0, 且为等势点
- 单相中与中性点之间的电压 UaN 即单相上结点的相电压
- 通过公式转换即可得到线电压(不同相之间对应节点的电压) Uab(或已知线电压, 计算相电压)
- 单相中的电流即线电流, 对于 Y形 电路, 区分无意义
- 等效回路中两个非中性点之间的电压无法转换(无意义)
Y-Δ
- 通过将 Δ 形负载转化为等效的 Y 形负载
- 由于负载对称, 满足关系
ZLΔ=31ZLY
- 通过单个负载的电流计算公式等价于相电流的转换公式, 对于 Y 型电源, 其相电流等于线电流
eg.
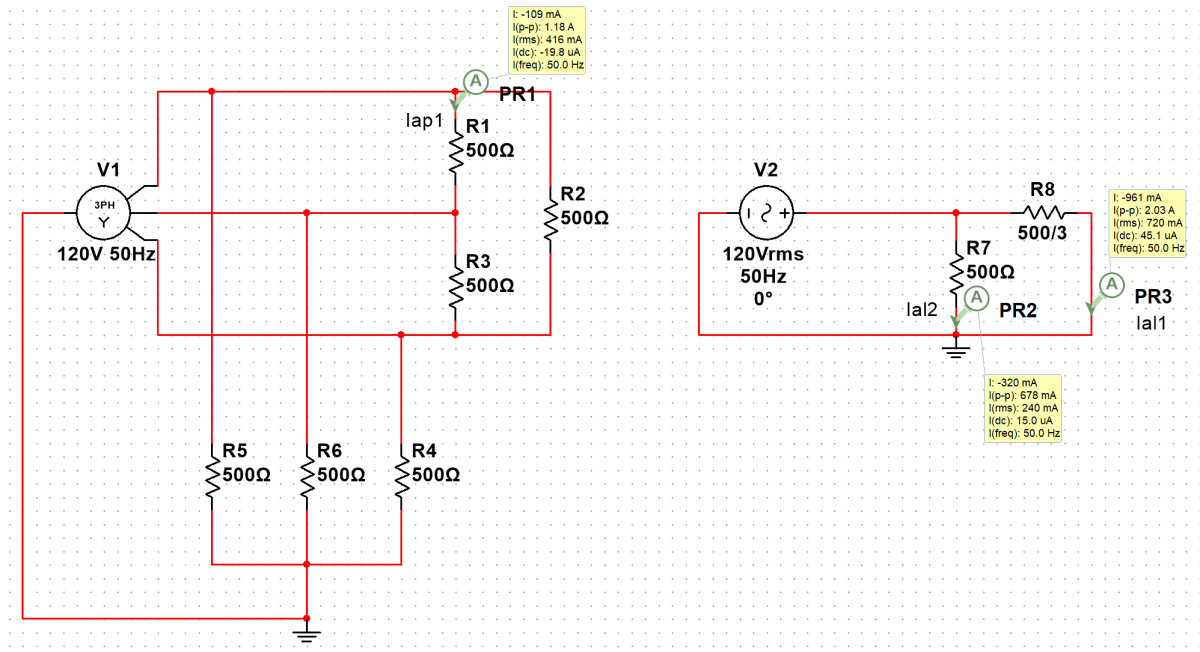
此电路中, 等效单相回路为两个负载并联, 且 Δ 负载上的电流为线电流 Ial1 , 单个负载上通过的实际电流为相电流 Iap1, 计算时需要转换
Δ-Δ
- 将Δ 形负载转化为等效的 Y 形负载, 再将 Δ 形电压源转化为等效的 Y 形电压源
- Δ 形电压源中的单相电压即线电压(电压源均在两个端口之间), 将其转为相电压即可使用分相法计算
对称三相电路的功率
功率公式
P=3UpIpcosϕ=3UlIlcosϕ
- 其他类型功率的计算类似, 均使用 3UpIp 或 3UlIl
- 功率因数, 其中 ϕ 为负载阻抗角
λ=cosϕ=SP
P单=UpIpcosϕ
计算注意
- 由于 Y 型电路中 Il 与 Ip 等价, 因此分相法中可直接使用 P=3UpIlcosϕ(不能直接对 Δ 负载使用)
- 分相法中的欧姆定律
U˙p=ZI˙l
- 题目中的电机功率均为三相总功率, 注意区分总功率(默认, 需要乘上系数)与单相功率
三相电路功率测量
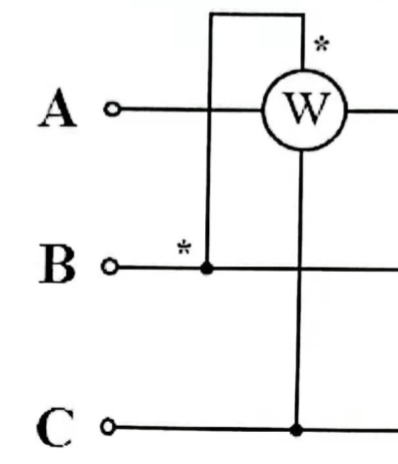
瓦特表无星号线测量的是电流流出端 / 电压负极
三瓦特表法
- 用于测量四线制三相电路 P=P1+P2+P3, 如果对称则 P1=P2=P3
- 瓦特表的引出线接在 N 上
两瓦特表法
非对称三相电路
电源对称时可使用以下方法:
- 有无负载的中性线 N 时, 仍可用分相法, 但三相要单独计算
- 其他情况可用节点分析法, 以 N 为接地点
- 线相电压转换关系依然满足
易错知识点
P1=P2
P1=Re[U˙acI˙a]=P2=Re[U˙bcI˙b]
注意 U˙ac 为 C 的线电压
根据接线的位置不同, 公式中 a 表示瓦特表所在相, c 表示瓦特表引出端相
当公式中出现 U˙ac 其值与 U˙ca 相反, U˙ac=−U˙ca=−U˙ab∠120∘
- 做题前明确题目中给出的是相电压还是线电压
- 三相电路的功率公式中, ϕ 通过 U˙p 与 I˙l 的夹角得到
P=3U˙lI˙lcos(ϕ)=3Re[U˙lI˙ˉl]
- 单相法中, Δ 负载中的电流等价于 Δ 电路中的线电流转相电流公式, 但不是相电流. Y−Y 电路中, 相线电流相同


