操作臂运动学

连杆参数与坐标系

在实际情况的操作臂中, 连杆可能是一个弯曲杆, 而关节具有复杂形状
但在建模时, 总将先提取出关节的轴线 (Axis) 为一条无限长的直线, 即操作臂旋转副 (Revolute Joint) 的转轴或平动副 (Prismatic Joint) 的平动方向
然后使用以下方法定义建模关节与连杆

• 定义基座开始的第一个轴线 $1$ 到末端的每个轴线依次编号至最后一个轴线 $n$
• 定义连杆 (Rod) 为一条有限长的线段 (或一个点), 连杆 $i-1$ 为轴线 $i-1$ 与轴线 $i$ 间的公垂线, 共有 $0\sim n$ 个关节
  • 最后一个轴线 $n$ 上的连杆 $n$ 则根据末端执行器要求定义
  • 有时定义基座为连杆 $0$, 其另一端点为与底面的固连点
• 规定关节 (Joint) 为一个点, 关节 $i-1$ 为轴线 $i-1$ 与连杆 $i-1$ 的交点, 共有 $1\sim n$ 个关节

注意, 以上建模产生的操作臂模型仅实际操作臂的轴线信息, 并不一定反应实际的关节与连杆

连杆坐标系

一般情况下通过如下方式规定连杆 $i-1$ 的坐标系

• 原点为关节 $i-1$ 的所在点
• $z$ 轴与轴线 $i-1$ 共线, 正方向可任意规定, 可先选择方便建模的一侧为正, 最后根据电机正转方向调整
• $x$ 轴与连杆 $i-1$ 共线, 以关节 $i-1$ 所在点指向关节 $i$ 所在点为正
• $y$ 轴通过 $z$ 轴到 $x$ 轴的右手定则确定

称连杆 $i-1$ 的坐标系为 $\{i-1\}$, 其中基座坐标系为 $\{0\}$

连杆参数

首先通过运动的方式描述坐标系之间的联系
即通过坐标系 $\{i-1\}$ 运动到坐标系 $\{i\}$ 的运动描述连杆参数

1. 绕运动坐标系 $x$ 轴正方向旋转角度 $\alpha_{\red{i-1}}$, 有运动算子 ${}^{b}\bm{R}(x, \alpha_{\red{i-1}})$, 通过该旋转使 $z$ 轴与轴线 $i$ 平行
2. 沿运动坐标系 $x$ 轴正方向移动距离 $a_{\red{i-1}}$, 有运动算子 ${}^{b}\bm{D}(x, a_{\red{i-1}})$
3. 绕运动坐标系 $z$ 轴正方向旋转角度 $\theta_{\blue{i}}$, 有运动算子 ${}^{b}\bm{R}(z, \theta_{\blue{i}})$, 通过该旋转使 $x$ 轴与连杆 $i$ 平行
4. 沿运动坐标系 $z$ 轴正方向移动距离 $d_{\blue{i}}$, 有运动算子 ${}^{b}\bm{D}(z, d_{\blue{i}})$

在实际中, 以上参数分别有以下含义

• $\alpha_{\red{i-1}}$ 表示轴线 $i-1$ 与 $i$ 之间的夹角, 该参数为一个与操作臂有关的常数
• $a_{\red{i-1}}$ 表示连杆 $i-1$ 的长度, 该参数为一个与操作臂有关的常数
• $\theta_{\blue{i}}$ 表示连杆 $i-1$ 与 $i$ 之间的夹角, 当关节为旋转副时, 连杆 $i$ 可绕轴线旋转, 因此是一个变量, 仅存在初始姿态偏置
• $d_{\blue{i}}$ 表示连杆 $i-1$ 与轴线 $i$ 交点与关节 $i$ 的距离, 当关节为移动副时, 关节 $i$ 可沿轴线平移, 因此是一个变量, 仅存在初始姿态偏置

以 $\alpha_{\red{i-1}},a_{\red{i-1}},\theta_{\blue{i}},d_{\blue{i}}$ 四个参数为一组, 每组参数都可以描述连杆坐标系 $\{i-1\}\to\{i\}$ 的关联, 对于一个 $n$ 关节的操作臂, 即需要 $n$ 组参数描述
并使用如下所示的连杆参数表表示

$\bm{i}$	$\bm{\alpha_{i-1}}$	$\bm{a_{i-1}}$	$\bm{\theta_{i}}$	$\bm{d_{i}}$	变化范围
$1$	$0^\circ$	$0$	$\theta_1(90^\circ)$	$0$	$-160^\circ\sim 160^\circ$
$2$	$-90^\circ$	$430$	$0^\circ$	$d_2(0)$	$0\sim 20$
$\dots$	$\dots$	$\dots$	$\dots$	$\dots$	$\dots$
$n$	$90^\circ$	$0$	$0$	$0$	$-266^\circ\sim 266^\circ$

其中

• 编号 $i$ 表明该行参数体现了坐标系 $\{i-1\}\to\{i\}$ 的参数, 或连杆 $i-1$ 的参数
• 对于不随运动改变的常量参数直接填写
• 对于变量参数则使用格式 $\theta_i(\dots)$, 即直接写出符号, 然后在括号内写入初始值
• 必要时可在最后加上该组参数中的变量参数的变化范围

操作臂建模的一般方法

$n$ 关节的操作臂建模即找出 $n\times 4$ 个连杆参数, 并写成连杆参数表

一般可遵循以下步骤

1. 保证操作臂处于特定状态, 保证尽可能多的连杆坐标系 $\{i\}$ 的三个坐标轴与固定坐标系的任一坐标轴平行
2. 确定并画出操作臂 $1\sim n$ 号的轴线, 使用双点划线表示, 并在末端编号 $A_{iR/P}$, 其中 $R$ 表示旋转副, $P$ 表示移动副 (画图时可采用斜二测画法, 且沿坐标轴方向的虚线表示点或轴线之间的位置关系)
3. 从坐标系 $\{0\}\to\{n\}$ 依次确定, 并在图上标出 $x,z$ 轴, 以及关节 $i$ 的运动方向及变量参数
   对于坐标系 $i-1$
   推荐先通过以下步骤, 在轴线图中找出各个关节坐标系的原点
   • 对于一般情况, 使用连杆坐标系的基本定义
     即以连杆 (轴线 $i-1$ 与 $i$ 的异面直线) 在轴线 $i-1$ 的交点为坐标原点, $z$ 轴沿轴线方向, $x$ 轴沿连杆方向, 以指向轴 $i$ 为正方向
   • 对于轴线 $i-1$ 与 $i$ 相交时, 连杆 $i-1$ 为一个点
     以交点为坐标系原点, $x$ 轴方向垂直于轴线 $i,i-1$, 即 $\bm{x}_{i-1}=\pm\bm{z_i}\times\bm{z_{i-1}}$
   • 对于轴线 $i-1$ 与 $i$ 平行时, 存在无数条合法的连杆 $i-1$
     可使用以下两种原则之一选择原点, 坐标轴方向确定同一般情况
     • 取轴线 $i-1$ 上与实际关节相关联的点为坐标系原点 (尽可能与实际关联原则, 此时 $d$ 根据实际选取)
     • 取连杆 $i-2$ 在轴线 $i-1$ 上的交点为坐标系原点 (尽可能多参数为 $0$ 原则, 此时 $d_{i-1}=0$)
   • 对于轴线 $i-1$ 与 $i$ 重合时, 存在无数条合法的连杆 $i-1$, 且均为点
     原点选择原则类似平行的情况, $x$ 轴尽可能与坐标系 $\{i-2\}$ 的 $x$ 或 $z$ 轴平行 (尽可能多参数为 $0,90^\circ$)
   • 对于基座坐标系 $\{0\}$, 可使用以下两种原则之一确定
     • 基座坐标系 $\{0\}$ 与坐标系 $\{1\}$ 重合 (尽可能多参数为 $0$ 原则, 此时第一组参数全为 $0$)
     • 基座坐标系 $\{0\}$ 的原点为轴线 $1$ 与地面的交点, $z$ 轴位于轴线 $1$ 上, $x$ 轴与参考坐标系的 $x$ 或 $z$ 轴平行 (尽可能与实际关联原则, 此时仅 $a_0,\alpha_0=0$)
   • 对于末端坐标系 $\{n\}$, $x$ 轴与坐标系 $\{n-1\}$ 的 $x$ 轴平行, 原点使用以下两种原则之一确定
     • 以连杆 $n-1$ 与轴线 $n$ 的交点为原点 (尽可能多参数为 $0$ 原则, 此时 $d_{n}=0$)
     • 根据实际情况选择轴线 $n$ 上与实际执行器相关联的点为原点 (尽可能与实际关联原则, 此时 $d$ 根据实际选取)
4. 根据坐标轴依次确定各组参数
   1. 单独画出坐标系 $\{i-1\}$ 与 $\{i\}$, 并且在接下来每步尽量画出中间坐标系
   2. 绕运动坐标系 $x$ 轴旋转 $\alpha_{i-1}$, 使其 $z$ 轴与 $z_{i}$ 平行
   3. 沿运动坐标系 $x$ 轴平移 $a_{i-1}$, 使坐标原点移动到轴线 $i$ 上
   4. 绕运动坐标系 $z$ 轴旋转 $\theta_{i}$, 使其 $x$ 轴与 $x_{i}$ 平行
   5. 沿运动坐标系 $z$ 轴平移 $d_i$, 使坐标原点与 $\{i\}$ 重合

简单来说建模应当遵守以下原则

1. 尽量使模型与实际相结合, 如坐标系原点的确定 (使用该原则时, 最好能使坐标系 $\{n\}$ 的原点与实际操作臂的末端重合)
2. 尽量使参数为 $0$ 或 $90^\circ$, 为上一原则的补充
3. 便于建模原则, 如坐标轴方向的确定
4. 如果已经给出了特定关节的坐标系, 特别是首末关节, 则优先使坐标系满足给出的要求

操作臂建模举例

对于如图所示的 PUMA560 机械臂

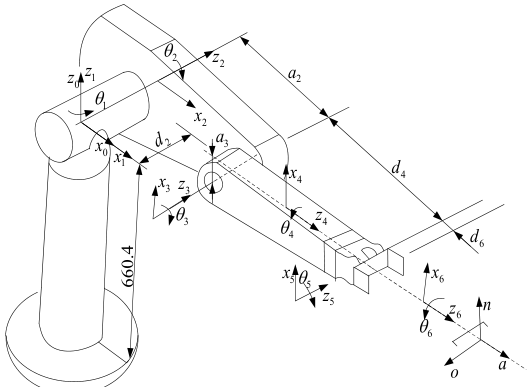
建模时按两步画出如下轴线与连杆坐标图

图中

• 坐标系 $\{0\}$ 使用尽可能为 $0$ 的原则, 使坐标系 $\{0\}$ 与 $\{1\}$ 重合
• 坐标系 $\{2\}$ 原点选取使用了与实际相符原则, 保证剩余的坐标系原点位于实际机械臂末端所在的 $YOZ$ 平面
• 注意坐标系 $\{3\}$ 与 $\{4\}$ 之间在 $\bm{x}_3$ 方向偏距 $a_3$ 来自轴线 $A_{3R},A_{4R}$ 之间的位置关系

由坐标系图可得到操作臂的连杆参数表

$\bm{i}$	$\bm{\alpha_{i-1}}$	$\bm{a_{i-1}}$	$\bm{\theta_{i}}$	$\bm{d_{i}}$
$1$	$0^\circ$	$0$	$\theta_1(0^\circ)$	$0$
$2$	$-90^\circ$	$0$	$\theta_1(0^\circ)$	$d_2$
$3$	$0^\circ$	$a_2$	$\theta_1(-90^\circ)$	$0$
$4$	$-90^\circ$	$a_3$	$\theta_1(0^\circ)$	$d_4$
$5$	$90^\circ$	$0$	$\theta_1(0^\circ)$	$0$
$6$	$-90^\circ$	$0$	$\theta_1(0^\circ)$	$0$

正向运动学

三种描述空间

对于三维空间中的 $n$ 关节操作臂, 定义三种描述空间

• 操作空间, 即包含了所有操作臂的末端位姿 $\bm{T}$ 的空间, 由于是在三维空间中, 因此操作空间共有位置与姿态共 6 个独立参数
• 关节空间, 由操作臂 $n$ 个关节变量 $q_i$ (将旋转变量 $\theta_i$ 与平动变量 $d_i$ 变量统称为 $q_i$) 组成的空间, 关节空间包含了所有关节变量组成的矢量 $\bm{q}$
• 驱动空间, 对于非直接驱动的操作臂, 从驱动器的驱动量 $s_i$ 到关节变量 $q_i$ 还需要经过一次传动机构的转换. 驱动空间即由这 $n$ 个驱动量组成 (对于简单的直接驱动操作臂可以不考虑)

通过运动学方程 $\bm{T}=\bm{T}(\bm{q})$ 可实现关节空间到操作空间的映射, 即正向运动学
相反求出操作空间到关节空间的映射为反向运动学, 即已知末端姿态 $\bm{T}$, 求出关节变量 $\bm{q}$

坐标系规定

在操作臂的实际使用中, 通常定义如下坐标系

• $\{\bm{B}\}$ 基座标系 Base, 即关节坐标系 $\{0\}$
• $\{\bm{W}\}$ 手腕坐标系 Wrist, 即末端关节坐标系 $\{n\}$
  • 与基座标系间存在关系 ${}^{B}_{W}\bm{T}={}^{0}_{n}\bm{T}(\bm{q})$
• $\{\bm{S}\}$ 工作站坐标系 Station, 通常固接在工作台角点上, 用于规划路径时描述操作臂的姿态, 因此也成为固定坐标系或作业坐标系
  • 通常通过基座标系定义, 并作为不变的已知条件 ${}^{B}_{S}\bm{T}$
• $\{\bm{T}\}$ 工具坐标系 Tool, 固接在末端执行器端部 (对于手爪则为两指的终点) 的坐标系, 以表示末端执行其的位姿
  • 通常通过手腕座标系定义, 并作为不变的已知条件 ${}^{W}_{T}\bm{T}$
• $\{\bm{G}\}$ 目标坐标系 Goal, 用于描述机器人末端执行其应当达到的位姿, 通常运动结束时应当与 $\{T\}$ 重合
  • 通常通过工作站标系定义, 在反解时作为已知条件 ${}^{S}_{T}\bm{T}$

连杆变换矩阵

由连杆参数以及通过运动描述位姿可知, 对于在连杆坐标系 $\{i-1\}$ 下描述坐标系 $\{i\}$ 时有齐次矩阵

$$\bm{T}_{i-1 \to i}=\space^{i-1}_{i}\bm{T}(q_i)={}^{b}\bm{R}(x, \alpha_{\red{i-1}}){}^{b}\bm{D}(x, a_{\red{i-1}}){}^{b}\bm{R}(z, \theta_{\blue{i}}){}^{b}\bm{D}(z, d_{\blue{i}})$$

根据坐标系变换方法, 组合各个连杆间的齐次矩阵, 即可得到正向运动学的运动方程

$${}^{B}_{W}\bm{T}={}^{0}_{n}\bm{T}(\bm{q})={}^{0}_{1}(q_1)\bm{T}{}^{1}_{2}(q_2)\bm{T}\dots\space^{n-2}_{n-1}(q_{n-1})\bm{T}\space^{n-1}_{n}\bm{T}(q_n)$$

对于同一个操作臂, 无论连杆参数如何选择, 只要坐标系 $\{0\},\{n\}$ 相同, 都能得到相同的正向运动学方程 ${}^{B}_{W}\bm{T}={}^{0}_{n}\bm{T}(\bm{q})$

当关节位移带有偏置时, 如果要使用新的参数注意代换 $q_i=q_i'+s_{o}$, 即以带偏置的关节位移 $q'_i$ 代换变换矩阵中的原位移 $q_i$
例如带偏置的旋转关节 $\theta_i(90^\circ)$, 则有 $q_i+90^\circ=\theta_i$, 在变换矩阵中 (可以在最后才带入代换)

$$\begin{cases} \sin(\theta_i)\to\sin(q_i+90^\circ)=\cos(q_i)\\ \cos(\theta_i)\to\cos(q_i+90^\circ)=-\sin(q_i) \end{cases}$$

逆向运动学

逆向运动学的解

对于正向运动学, 对于一组给定的关节变量 $\bm{q}$, 能得到唯一对应的末端姿态 ${}^{B}_{W}\bm{T}$
但对于逆向运动学的解 (也称为反解), 往往存在多个解或是无解的情况

逆向运动学解的解析性

由于逆向运动学通常涉及超越方程, 因此可能不存在解析解, 只有数值解
为了保证工业机器人能灵活求出反解, 要求满足以下解析解存在的充分条件之一 (Pieper 准则)

• 三个相邻关节交于一点
• 三个相邻关节轴线平行

逆向运动学的可解性

将操作空间中, 由存在反解的点所构成的区域称为工作空间, 并且再进一步分为以下两种

• 灵活操作空间 操作臂的末端执行器能以任意姿态到达该区域中的任意一点
• 可达空间 操作臂的末端执行器能以至少一个姿态达到该区域中的一点

通常

• 灵活操作空间时可达空间的一个子集, 一般可达空间由灵活操作空间与操作臂奇异位姿所在点 (奇异点) 组成
• 在三维中, 如果机器人的自由度小于 $6$, 则其不存在灵活操作空间

逆向运动学解的多解性

逆向运动可解时, 还存在多解的问题, 通常需要在多解中寻找一个最优解
为了让运动更灵活, 工业机器人也会刻意设计使其解尽量多

• 由于翻转问题, 操作臂中相邻的连杆长度 $a_i,a_{i+2}$ 为零的连杆越多, 离散解越少
  当所有连杆长度均不为 $0$, 最多有 $16$ 个反解
• 当操作臂的关节数大于 $6$, 表明其具有冗余的自由度, 此时操作臂将具有无穷个连续的反解

PUMA560 的 Pieper 反解

对于 PUMA560, 由其连杆参数可知, 该操作臂满足 Pieper 条件, 因此逆向运动学存在解析解

由于该操作臂的最后三个关节 $4, 5, 6$ 的原点重合, 不存在任何平移, 因此齐次矩阵 ${}^{3}_{6}\bm{T}(\theta_4,\theta_5,\theta_6)$ 仅与操作臂的手腕 $\{\bm{W}\}$ 姿态有关, 且矩阵 ${}^{3}_{6}\bm{T}$ 的第四列向量 ${}^{3}\bm{p}_{6o}={}^{3}\bm{p}_{4o}$ 为一个仅与关节参数 $\alpha_3,a_3,d_4$ 有关的常量

因此可得, 操作臂的手腕位置仅由变量 $\theta_1,\theta_2,\theta_3$ 决定, 可将运动学反解分为两步

• 第一步通过给定腕部位置 ${}^{0}\bm{p}_{6o}$ 解出参数 $\theta_1,\theta_2,\theta_3$
• 结合已解出参数 $\theta_1,\theta_2,\theta_3$ 与腕部姿态 ${}^{0}_{6}\bm{R}$ 解出参数 $\theta_4,\theta_5,\theta_6$

腕部位置反解

腕部位置分解即求解方程

$${}^{0}\bm{p}_{6o}={}^{0}\bm{p}_{4o}={}^{0}_{1}\bm{T}(\theta_1){}^{1}_{2}\bm{T}(\theta_2){}^{2}_{3}\bm{T}(\theta_3){}^{3}\bm{p}_{4o}$$

具体求解过程省略, 求解方程如下

有关中间变量

首先规定如下一组仅与变量 $\theta_3$ 有关的中间变量, 且有形式 $f=A\cos\theta_3+B\sin\theta_3+C$

$$\begin{cases} f_1(\theta_3)=a_3c_{\theta_3}+d_4s_{\alpha_3}s_{\theta_3}+a_2\\ f_2(\theta_3)=a_3c_{\alpha_2}s_{\theta_3}-d_4s_{\alpha_3}c_{\alpha_2}c_{\theta_3}-d_4s_{\alpha_2}c_{\alpha_3}-d_3s_{\alpha_2}\\ f_3(\theta_3)=a_3s_{\alpha_2}s_{\theta_3}-d_4s_{\alpha_3}s_{\alpha_2}c_{\theta_3}+d_4c_{\alpha_2}c_{\alpha_3}+d_3c_{\alpha_2} \end{cases}$$

然后对应如下一组仅与中间变量 $f_1,f_2,f_3$ 有关的中间变量

$$\begin{cases} k_1=f_1\\ k_2=-f_2\\ k_3=f_1^2+f_2^2+f_3^2+a_1^2+d_2^2+2d_2f_3\\ k_4=f_3c_{\alpha_1}+d_2c_{\alpha_1} \end{cases}$$

θ3 与 θ2 求解

有如下关于 $\theta_3,\theta_2$ 的方程 (其中 $\begin{Vmatrix}{}^{0}\bm{p}_{6o}\end{Vmatrix}^2=r^2,{}^{0}z_{6o}=z$)

$$\begin{cases} r^2=2a_1(k_1\cos\theta_2+k_2\sin\theta_2)+k_3\\ z=\sin\alpha_1(k_1\sin\theta_2-k_2\cos\theta_2)+k_4 \end{cases}$$

• 当 $a_1=0$ 或 $\sin\alpha_1=0$, 其中一个方程退化为仅与 $\theta_3$ 有关, 以此可解出 $\theta_3$
• 对于一般情况, 可消去 $\theta_2$ 得到仅与 $\theta_3$ 有关的方程 $\frac{(r^2-k_3)^2}{4a_1^2}+\frac{(z-k_4)^2}{\sin^2\alpha_1}=k_1^2+k_2^2$

在实际求解 $\theta_3$ 时, 一般还会定义变量 $u=\frac{\tan\theta_3}{2}$ 转换方程中的三角函数, 使方程完全转换为关于 $u$ 的四次方程
转换公式如下

$$u=\tan\frac{\theta_3}{2},\;\cos\theta_3=\frac{1-u^2}{1+u^2},\;\sin\theta_3=\frac{2u}{1+u^2}$$

根据上述关于 $\theta_3,\theta_2$ 的方程组可得 (注意该笔记中四象限反正切的定义与常见相反)

$$\begin{cases} m=\frac{r^2-k_3}{2a_1}\\ n=\frac{z-k_4}{\sin(\alpha_1)}\\ b=\frac{k1}{k2}+\frac{k2}{k1} \end{cases}\to \begin{split} \theta_2&=\operatorname{Arctan}[(\frac{m}{k2}-\frac{n}{k1})/b,(\frac{m}{k1}+\frac{n}{k2})/b]\\ &=\operatorname{Arctan}[mk_1-nk_2,mk_2+nk_1] \end{split}$$

$\theta_2$ 通过分式上下乘以 $k_1k_2$ 得到, 并通分消去分母 $k_1^2+k_2^2\ge 0$

θ1 求解

对于 $\theta_1$ 的求解还需要引入以下两个与 $\theta_2,f$ 有关的中间变量 (带入之前求解结果 $\theta_2,\theta_3$ 即可得出)

$$\begin{cases} g_1=f_1c_{\theta_2}-f_2s_{\theta_2}+a_1\\ g_2=f_1c_{\alpha_1}s_{\theta_2}+f_2s_{\alpha_1}c_{\theta_2}-f_3s_{\alpha_1}-d_2s_{\alpha_1} \end{cases}$$

$\theta_1$ 满足方程组 (其中 ${}^{0}x_{6o}=x,{}^{0}x_{6o}=y$)

$$\begin{cases} x=g_1c_{\theta_1}-g_2s_{\theta_1}\\ y=g_1s_{\theta_1}+g_2c_{\theta_1}\\ b=\frac{g1}{g2}+\frac{g2}{g1} \end{cases}\to \begin{split} \theta_1&=\operatorname{Arctan}[(\frac{y}{g_1}+\frac{x}{g_2})/b, (\frac{y}{g_2}-\frac{x}{g_1})/b]\\ &=\operatorname{Arctan}[yg_2+xg_1,yg_1-xg_2] \end{split}$$

腕部姿态反解

不考虑原点位置, 仅考虑姿态 $\bm{R}$, 由操作臂结构可知, 运动方程中, 仅 ${}^{3}_{6}\bm{R}$ 与最后三个关节变量 $\theta_4,\theta_5,\theta_6$ 有关
又由于 $\theta_1,\theta_2,\theta_3$ 已通过腕部位置反解得到, 腕部姿态 ${}^{0}_{6}\bm{R}$ 为已知的反解条件, 有

$$\begin{split} {}^{0}_{6}\bm{R}&={}^{0}_{3}\bm{R}{}^{3}_{6}\bm{R}\\ {}^{0}_{3}\bm{R}^T{}^{0}_{6}\bm{R}&={}^{3}_{6}\bm{R} \end{split}$$

由连杆变换矩阵可得, 姿态矩阵 ${}^{3}_{6}\bm{R}$ 由连续三次的, 每次绕运动坐标系的 $x,z$ 轴旋转

如图所示, 对于姿态矩阵 ${}^{3}_{6}\bm{R}$ 有如下特点

• 由于 $\alpha_4,\alpha_5=\pm 90^\circ$
  • 取 $90^\circ$ 时, 相当于将 $z$ 轴移动到 $y$ 轴位置, $y$ 轴移动到 $-z$ 轴位置
  • 取 $-90^\circ$ 时, 相当于将 $y$ 轴移动到 $z$ 轴位置, $z$ 轴移动到 $-y$ 轴位置
• 对于如上图所示的情况, 上方为一般旋转过程, 下方为忽略 $\alpha$ 的旋转, 即 $zyz$ 欧拉角
  • $\theta_4$ 即绕经过 $\alpha_3$ 旋转后的 $z_4'$ 旋转
  • $\theta_5$ 绕 $z_5'$ 旋转相当于绕运动坐标系的 $-y$ 旋转
  • $\theta_6$ 绕 $z_6'$ 旋转相当于绕运动坐标系的 $z$ 旋转
  • 因此将绕经过 $\alpha_3$ 旋转后的坐标系为起点, 得到目标坐标系 ${}^{0}_{6}$ 相当于经历一次 $zyz$ 的欧拉角
    对于图示情况, 有 $\bm{R}_{zyz}(\theta_4, -\theta_5, \theta_6)=\bm{R}(x,\alpha_3)^T{}^{3}_{6}\bm{R}$
• 根据 $\alpha_4,\alpha_5$ 取值的正负决定了 $\theta_5, \theta_6$ 与欧拉角求解结果 $\beta,\gamma$ 之间的关系
  • 当 $\alpha_4=90^\circ,\alpha_5=-90^\circ$, 另外两个参数对应, 但 $\theta_5=-\beta$
  • 当 $\alpha_4=-90^\circ,\alpha_5=90^\circ$, 腕部关节参数与欧拉角参数一一对应
  • 剩余情况可使用如图所示的方法推断
• 在使用欧拉角求解 $\theta_4, \theta_5, \theta_6$ 前, 应当对 ${}^{3}_{6}\bm{R}$ 右乘 $\bm{R}(x,\alpha_3)^T$ 以消除 $\alpha_3$ 的影响, 保证剩余的部分为标准 $zyz$ 约定的欧拉角

类似的有数学证明 带入 $^{3}_{6}\bm{R}$

$$\begin{split} \bm{R}^T(x,\alpha_3)^{3}_{6}\bm{R}&=\bm{R}(z,\theta_4)[\bm{R}(x,90^\circ)\bm{R}(z,\theta_5)][\bm{R}(x,-90^\circ)\bm{R}(z,\theta_5)]\\ &=\bm{R}(z,\theta_4)\begin{bmatrix} \cos\theta_5&-\sin\theta_5&0\\ 0&0&-1\\ \sin\theta_5&\cos\theta_5&0 \end{bmatrix}\begin{bmatrix} \cos\theta_6&-\sin\theta_6&0\\ 0&0&1\\ -\sin\theta_6&-\cos\theta_6&0 \end{bmatrix} \end{split}$$

与 $zyz$ 欧拉角对比 列与行的相似性 置换矩阵自身为逆

$$\begin{split} \bm{R}_{zyz}(\alpha,\beta,\gamma)&=\bm{R}(z,\alpha)\bm{R}(y,\beta)\bm{R}(z,\gamma)\\ &=\bm{R}(z,\alpha) \Bigg( \begin{bmatrix} \cos\beta&0&\sin\beta\\ 0&1&0\\ -\sin\beta&0&\cos\beta \end{bmatrix} \begin{bmatrix} 1&0&0\\ 0&0&-1\\ 0&1&0 \end{bmatrix} \Bigg) \Bigg( \begin{bmatrix} 1&0&0\\ 0&0&1\\ 0&-1&0 \end{bmatrix} \begin{bmatrix} \cos\gamma&-\sin\gamma&0\\ \sin\gamma&\cos\gamma&0\\ 0&0&1 \end{bmatrix} \Bigg)\\ &=\bm{R}(z,\alpha)\begin{bmatrix} \cos\beta&\sin\beta&0\\ 0&0&-1\\ -\sin\beta&\cos\beta&0 \end{bmatrix}\begin{bmatrix} \cos\gamma&-\sin\gamma&0\\ 0&0&1\\ -\sin\gamma&-\cos\gamma&0 \end{bmatrix} \end{split}$$

可得 $\alpha=\theta_4,\beta=-\theta_5,\gamma=\theta_6$

由姿态矩阵求解 $zyz$ 欧拉角参数 $\bm{R}_{zyz}(\alpha,\beta,\gamma)$ 时有公式 (当 $\beta=0,180^\circ$, 关节处于奇异状态, 一般取 $\alpha=0,\gamma=\operatorname{Arctan}(r_{11},-r_{12})$)

$$\begin{cases} \beta=\operatorname{Arctan}(r_{33},\sqrt{r_{31}^2+r_{32}^2})\\ \alpha=\operatorname{Arctan}(r_{13},r_{23})\\ \gamma=\operatorname{Arctan}(-r_{31},r_{32}) \end{cases}$$

根据 $\bm{R}_{zyz}(\alpha,\beta,\gamma)=\bm{R}(x,\alpha_3)^T{}^{3}_{6}\bm{R}$ 解出 $\alpha,\beta,\gamma$
再根据 $\alpha_4,\alpha_5$ 确定 $\theta_4, \theta_5, \theta_6$ 与 $\alpha,\beta,\gamma$ 的关系, 完成腕部的反解

通过翻转腕部, 还存在一组反解与原始解存在关系

$$\theta_4'=\theta_4+180^\circ,\theta_5'=-\theta_5,\theta_6'=\theta_6+180^\circ$$

因此 PUMA560 共有 $4\times 2=8$ 种不同的反解结果

PUMA560 的 Paul 反解