跳至主要內容

PID

大约 1 分钟

PID

注意

该笔记仅在旧笔记的基础上进行归类, 尚未对格式进行修复

通过改变输出量, 使输入量达到目标值 有关教程open in new window

U(t)=KPerr(t)+KIT∫err(t)dt+TKDderr(t)dt U(t)=K_P err(t)+\frac{K_I}{T}\int err(t)dt+TK_D\frac{d err(t)}{dt}

名词

  1. U(t)U(t) 输出量
  2. N(t)N(t) 输入量(需要控制的量)
  3. err(t)=N目标(t)−N实际(t)err(t)=N_{\text{目标}}(t)-N_{\text{实际}}(t) 输入量误差
  4. TT 系统经过的时间
  5. PP proportion 比例
  6. II integration 积分
  7. DD differentiation 微分
  8. KK 系数

比例控制算法

U(t)=KPerr(t) U(t)=K_P err(t)

当有阻力消耗时, 存在稳态误差, 无法达到目标值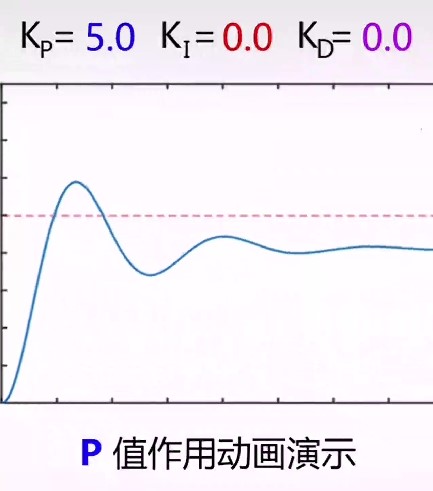

积分控制算法

U(t)=KPerr(t)+KIT∫err(t)dt U(t)=K_P err(t)+\frac{K_I}{T}\int err(t)dt

将前面若干次的误差进行累计，可以很好的消除稳态误差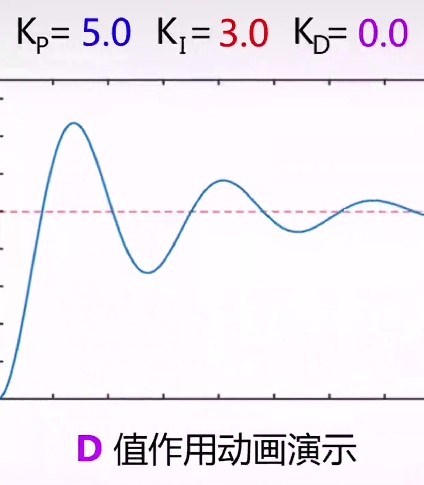

微分控制算法

U(t)=KPerr(t)+KIT∫err(t)dt+TKDderr(t)dt U(t)=K_P err(t)+\frac{K_I}{T}\int err(t)dt+TK_D\frac{d err(t)}{dt}

可以防止实际输入量超过目标输入量，即减少控制过程中的震荡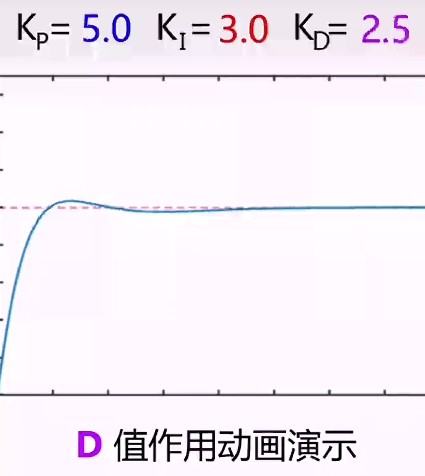

离散化

  1. 积分的离散化

KIT∫err(t)dt=KIT∑err(t)dT=KI∑err(t) \frac{K_I}{T}\int err(t)dt=\frac{K_I}{T}\sum err(t)dT=K_I\sum err(t)

  1. 微分的离散化

TKDderr(t)dt=KD[err(t)−err(t−dt)]Tdt=KD[err(t)−err(t−dt)] TK_D\frac{d err(t)}{dt}=K_D[err(t)-err(t-dt)]\frac{T}{dt}\\=K_D[err(t)-err(t-dt)]

  1. 离散化的总公式

U(t)=KPerr(t)+KI∑err(t)+KD[err(t)−err(t−dt)] U(t)\\=K_P err(t)+K_I\sum err(t)+K_D[err(t)-err(t-dt)]

具体使用

对于系数 KPK_P, KIK_I, KDK_D 均需要通过实验得到, 且积分控制与微分控制在部分情况下并不是必须的