人工神经网络

神经元运算

逻辑运算

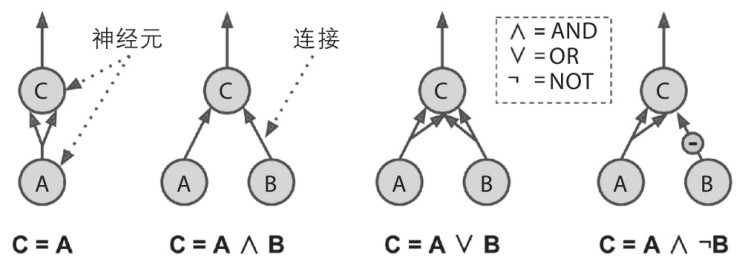
1. 简单神经元模型, 一个神经元具有多个输入与一个输出, 当两个以上输入激活时, 输出激活
2. 理论上可用此完成任何逻辑运算

感知器 TLU

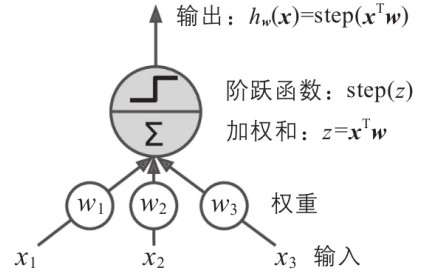
• 输入与输出为数字
• 每个输入连接与权重关联, 先计算加权和 $z=\sum w_ix_i$ , 然后进入阶跃函数
• 阶跃函数通常形式为

$$step(z)=\begin{cases}0,&z<0\\1,&z\ge 0\end{cases}$$

感知器训练

感知器一次被送入一个训练实例, 当预测结果与训练实例相同, 将增大权重, 反之权重将降低

$$w_{i,j}^{(next)}=w_{i,j}+\eta(y_j-\hat{y_j})x_i$$

• $y_j$ 为当前神经元的目标输出
• $\hat{y_j}$ 为当前神经元的目标输出
• $w_{i,j}$ 为第 $i$ 个输入神经元与第 $j$ 个输出神经元之间的连接权重
• $\eta$ 为学习率

单层感知器

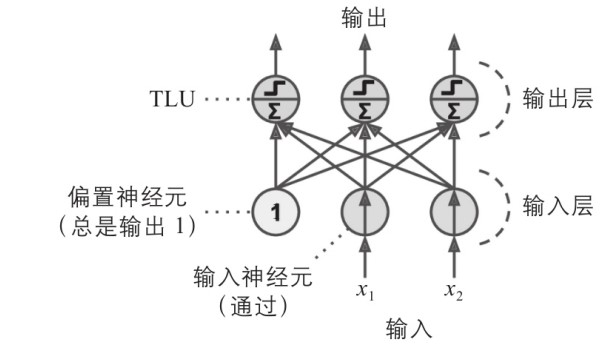
• 当一层中的所有神经元都连接到上一层中的每个神经元 (即其输入神经元) 时，该层称为全连接层或密集层
• 通常使用偏置神经元的特殊类型的神经元输出 1, 用于表示额外的偏置特征
• 可通过线性代数计算全连接层的输出 $h(X)=\phi(XW+b)$
  • $X$ 以实例为行, 特征 (输入值) 为列的输入矩阵
  • $W$ 以输入神经元为行, 人工神经元为列的权重矩阵
  • $\phi()$ 为激活函数, 对于感知器使用阶跃函数

多层感知器 MLP

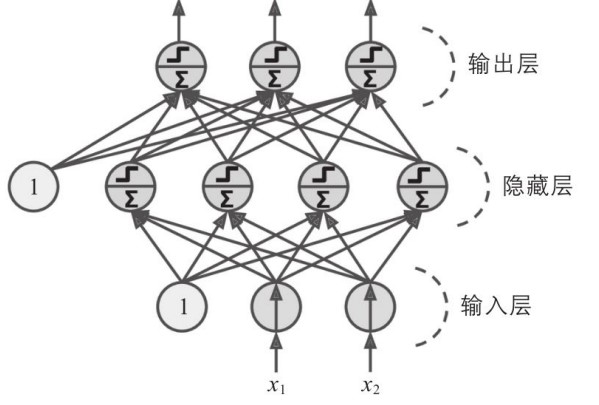
1. 单层感知器仅能处理小部分问题, 需要堆叠感知器, 消除其局限性
2. 通过堆叠感知器, 可以提高性能
3. 当神经网络包含隐藏层时, 称为深度神经网络

训练 MLP

1. 通过反向传播算法, 可以训练 MLP, 其过程如下
   1. 一次处理小批量 (batch) 实例, 通常为 32 个, 并且多次遍历整个训练集, 每次遍历称为一个轮次 (epoch)
   2. 将每个小批量的数据送入神经网络, 记录下所有中间结果 (正向传递)
   3. 使用损失函数 (通常为均方根误差) 测量网络的误差
   4. 计算每个输出连接对于误差的贡献, 并不断往下测量, 直到输入层为止 (反向传递)
   5. 使用计算得到的误差梯度来调整连接权重
2. 为了使训练过程更快, 通常会以随机权重初始化隐藏层的连接权重, 破坏对称性
3. 为了能够计算输出连接对于误差的贡献 (通过微分的方式), 激活函数需要能够微分, 因此不能使用阶跃函数, 而采用 s 型的其他函数
   1. $Sigmoid$ 函数 $\sigma(z)=\frac{1}{1+e^{-z}}$
   2. 双曲正切型函数 $tanh(z)=\frac{2}{1+e^{-2z}}-1$
   3. 线性整流函数 $ReLU(z)=max(0,z)$, 函数在 $z=0$ 不可微分, 在 $z<0$ 恒为 $0$, 但计算快速, 通常为默认的激活函数
4. 由于采用了非阶跃函数, 此时神经网络能够输出如浮点型等不同的结果

回归问题 MLP

1. 对于每一个输入需要一个输入神经元, 输出相同
2. 可对输入 / 输出神经元采用特定的激活函数, 限制其取值, 也可不采用激活函数
3. 损失函数通常为均方误差

分类问题 MLP

1. 对于每个类别可以设计一个输出神经元, 输出属于此类别的概率
2. 当类别确定时, 为了保证概率之和为 1, 可通过 softmax 函数保证
3. 由于分类属于概率问题, 因此通常采用交叉熵作为损失函数

Keras 实现 MLP

创建 Sequential 模型

model = keras.models.Sequential([
    keras.layers.Flatten(input_shape=[28, 28]),
    keras.layers.Dense(300, activation="relu"),
    keras.layers.Dense(100, activation="relu"),
    keras.layers.Dense(10, activation="softmax")
])

1. Sequential 模型是用于神经网络的最简单的 Keras 模型, 它仅由顺序连接的单层堆栈组成
2. 通过一个数组将模型中的各层按顺序传入模型
3. 对于模型的第一层即输入层, 输入层通常只是对数据预处理, 输入层中需要通过参数 input_shape 指定输入格式
4. 在确定模型的各层时, 还需要通过参数 activation 指定采用的激活函数
5. 激活函数的完整列表 https://keras.io/activations/

查看模型

1. 使用模型的 summary() 方法显示模型的所有层, 以及各层的参数 (即连接权重)
2. 通过索引访问模型的 layerw 成员, 可以访问模型的各层
3. 使用模型各层的 get_weights() 和 set_weights() 方法访问层的所有参数

设置模型

1. 调用模型的 compile() 方法, 来指定模型训练时的损失函数与优化器, 以及计算指标
2. 参数 loss 用于选择损失函数
3. 参数 optimizer 用于指定优化器
4. 参数 metrics 用于指定指标
5. 损失函数, 优化器和指标的完整列表参见
   1. https://keras.io/losses
   2. https://keras.io/optimizers
   3. https://keras.io/metrics

model.compile(
    loss="sparse_categorical_crossentropy",
    optimizer="sgd",
    metrics=["accuracy"]) 

训练模型

1. 调用模型的 fit 方法, 可以开始对模型进行训练
2. fit 方法将返回一个 History 对象, 包含了训练参数与每个轮次的信息
3. 可通过 pd.DataFrame(history.history) 将其转为 DtaFrame 对象, 并绘制
4. 将输入特征和目标类以及训练次数传入, 即可开始训练
5. 参数 validation_data 可用于传入验证集的数据, 需要用元组包括

history = model.fit(
    X_train, y_train, epochs=30,
    validation_data=(X_valid, y_valid))

使用模型进行预测与评估

1. 调用模型的 predict 方法可以使用模型对输入进行预测, 返回的结果将保存在 np.ndarray 中
2. 通常会使用数据集中的预测集 (valid set) 进行

训练深度神经网络

梯度爆炸与消失

1. 梯度消失 反向传播过程中, 随着误差向下传播, 梯度越来越小, 导致较低层的权重几乎不会被更新
2. 梯度爆炸 反向传播时, 可能相反, 梯度可能越来越大
3. 因此深度神经网络很容易受梯度不稳定的影响, 不同层的学习速度不同

TensorFlow 预处理数据

独热向量

1. 独热向量可用于编码特征, 以便于像数值一样, 计算特征之间的距离等
2. 独热向量为一个 n 维的向量 (n 为特征总数), 且取值仅为 0 或 1 (对于向量的每个位置, 分别表示一个特征)
3. 此时向量的距离可以较好的表示各个特征间的区别
4. 独热向量一般仅用于各个特点区别大的分类特征, 且总类别数最好小于 50

独热向量编码分类特征

vocab = ["<1H OCEAN", "INLAND", "NEAR OCEAN", "NEAR BAY", "ISLAND"]
indices = tf.range(len(vocab), dtype=tf.int64)
table_init = tf.lookup.KeyValueTensorInitializer(vocab, indices)
num_oov_buckets = 2
table = tf.lookup.StaticVocabularyTable(table_init, num_oov_buckets)

# 送入词汇表的数据集
categories = tf.constant(["NEAR BAY", "DESERT", "INLAND", "INLAND"])
cat_indices = table.lookup(categories)
cat_one_hot = tf.one_hot(cat_indices, depth=len(vocab) + num_oov_buckets)

1. 先通过 Tensorflow 的查找表将分类编码为查找表中的索引, 然后根据索引编码为独热向量
2. 首先定义词汇表, 表示一个特征下所有可能的类别
3. 根据词汇表, 为每个词创建索引
4. 通过 KeyValueTensorInitializer 对查找表初始化
5. 确定词汇表外 outof-vocabulary，oov 桶的数量, 可用于归类词汇表外的未知类别 (样本中可能出现部分未知的类别), 如果 oov 桶数量不足将导致冲突
6. 将数据送放入词汇表后, 可得到各个词汇的索引, 通过 one_hot 将索引转换为独热向量

使用嵌入编码分类特征

1. 嵌入是一种表示类别的可训练的密集向量
2. 通常嵌入为随机初始化的, 但通过训练, 如神经网络等, 嵌入的值会得到改善
3. 例如对于词嵌入, 通过训练, 相似的词之间距离更近, 并且能对语义进行计算
4. 嵌入向量的大小属于可调的超参数, 通常向量长度为 10 ~ 300

循环神经网络 RNN

循环神经元

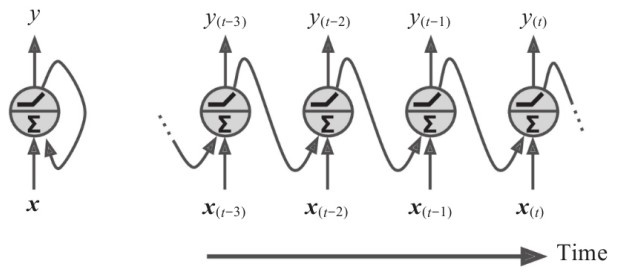
除了接收输入 $x^{(t)}$, 循环神经网络的神经元还接收前一个时刻的输出 $y^{(t-1)}$

单层循环神经网络

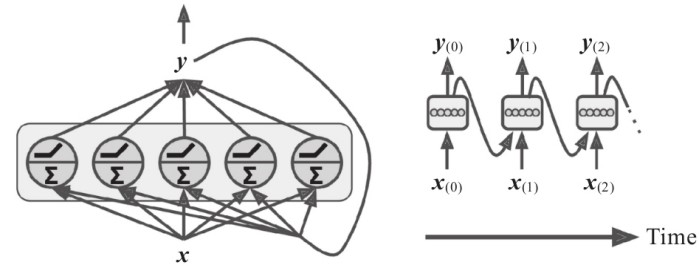
• 此时还有同一层中输出值与同一层中各个神经元之间的权重需要考虑
• 注意图中 $x$ 与 $y$ 为向量, $x$ 长度为输入神经元个数, $y$ 长度为输出神经元个数

记忆单元

• 由于循环神经元接收前一个时刻的输出的特性, 其具有记忆功能, 神经网络的输出与之前所有时刻的输入有关
• 单层的循环神经网络记忆能力有限, 一般仅有十个步长之内的记忆
• 通常 RNN 采用双曲正切函数作为激活函数, 而不是 $ReLU$

输入序列与输出序列

1. RNN 可以同时接收序列, 然后输出序列 (序列即一个与时刻 $t$ 有关的向量函数)
2. 通常序列可以是某个变量的变化, 或者一段文字
3. 可以仅采用最后一个输出量, 实现序列到向量的网络, 用于对评论与文章等的评估
4. 可以不断提供相同的输入量, 实现向量到序列的网络, 用于输入图片, 输出对图像的描述
5. 可以采用两个循环神经网络, 一个负责将句子编码为内部编码, 然后另一个将单词解码为另一种语言的句子, 可用于翻译

训练 RNN

• 同样采用常规的反向传播算法训练 RNN
• 由于 RNN 还与时间有关, 因此还要先沿时间展开网络
• 为了比较 RNN 的效果, 通常会训练一个单层的 MLP 用于比较

处理长序列的 RNN

不稳定梯度

短期记忆问题

可以处理比 RNN 更长的序列, 但对于更长的序列, 如长句子, 性能有限

LSTM 单元

1. 从外部来看, LSTM 与一般神经元一样有一个输入与一个输出
2. LSTM 与 RNN 的神经单元不同, 他使用两个状态来连接过去与当前时刻, 分别是长期状态 $c_{(t)}$ 与短期状态 $h_{(t)}$ (注意这些状态为向量, 对向量中的单个属性处理方式可能不同)
3. 单元中主要层为 $g_{(t)}$, 用于分析输入 $x_{(t)}$ 与上一个短期状态 (即输出) $h_{(t)}$, 与 RNN 相同, 但结果不直接输出, 而是经过另外三个逻辑门 $f,i,o$ 的处理
4. 另外三个逻辑门 $f,i,o$ 采用逻辑激活函数 (sigmoid), 输出范围为 $(0,1)$ 用于控制各个量的影响程度
   1. 遗忘门 $f$, 用于控制 $c_{t}$ 中的重要部分
   2. 输入门 $i$, 用于控制添加到长期状态的部分
   3. 输出门 $o$, 用于控制添加到输出的部分
5. 由 $h_{(t-1)}$ 与 $x_{(t)}$ 到各个门均有不同的权重参数

GRU 单元

$GRU$ 单元为 $LSTM$ 单元的简化版

1. 将两个状态向量合并为一个向量 $h_{(t)}$
2. 使用单个门控制遗忘与输入, 其中遗忘与输入之间的系数满足相加等于 $0$ 的关系 (通过 $1-z_{(t)}$ 控制), 此时满足规则, 如果记忆要存储, 则要剔除新的输入的影响
3. 没有输出门, 但使用控制门 $r$, 从上一个状态 $h_{(t-1)}$ 选择提供给主要门的部分